基（jī）於裝配的臥式加工中心精度建模與分析 -加工中（zhōng）心網-數控機床市場網

您現在的（de）位置：加工中心網（wǎng）> 技術前沿>基於裝配的臥式加（jiā）工中心精度建模與分析

基於裝配的臥式加工中心精度建模與分析

2017-12-13 來源：大連大（dà）學機（jī）械工程學院（yuàn）作者：李玉光

摘要：以多體係統理論為核心，運用齊次（cì）坐標（biāo）變換對（duì）臥式加工中心的精度問題進（jìn）行了係統、全麵的分析，重點立足於裝配中的精度建模（mó）和誤差分析。通過對加（jiā）工中（zhōng）心精度建模的（de）研究，揭示了利用齊次矩陣變換將誤差從機床部件傳遞到被加工零（líng）件的建模方法（fǎ），並對這（zhè）一方法進行總結，使其具（jù）有（yǒu）通用（yòng）性和方便性。最後（hòu）通過對某加工中心進行實（shí）例分析，驗證了（le）方法的可行性。

關鍵詞：加工中心；多體係統理（lǐ）論（lùn）；齊次坐標；精度建模

隨著現代機械製（zhì）造技術（shù）的飛速發展，精密和超精密加工技術成為現代機械（xiè）製造業的發展趨勢［1］。數控機床精度一直是影響其質量的核心問題，也是衡量機床水平的關（guān）鍵參數。因此，數（shù）控機床（chuáng）精度的研究受到了廣大學者的關注。我國目前的機床（chuáng）加工水平較世界發達國家還存在一定（dìng）的差距，提高我國數控（kòng）機床的（de）加工質量，研究數控機床的精度問題已成為一個重要的研究課題。

目前，我國生（shēng）產的數控機床約占國內市場份額的50％左右，中高（gāo）端數控機（jī）床市場的絕大部（bù）分被境外產品占領，其中高端數控機床國內產品（pǐn）的市場占有率僅（jǐn）4％左右［2］。造（zào）成這（zhè）種現象（xiàng）的主要原因是國產數控機（jī）床的（de）性能、加工精度、穩定性和可靠（kào）性等方麵都難（nán）以與國外高檔產（chǎn）品相比，其（qí）中加工精度是國產數控機床的（de）主要薄弱環節。

由於機床誤差而導致加工精度（dù）下降的（de）問題日（rì）益突出，如何對機床誤差進（jìn）行建模，進而補償甚至消除誤差成（chéng）為一項重（chóng）要的研究任務。

1 、誤差（chà）建模概述

機床（chuáng）精度在設計階段取決於兩個因素，一是零件（jiàn）的加工誤差，通過公差設計的控製可以減小加工誤差；二是裝（zhuāng）配工（gōng）藝，在（zài）裝配過（guò）程中會積累誤差。因此保（bǎo）障機床（chuáng）的精度，必須從公差分（fèn）析和裝配偏差入手，建（jiàn）立幾何精度表達和（hé）傳遞的數學模型［3］。

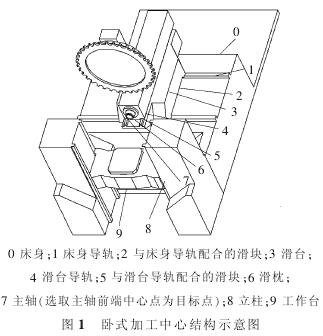
這樣可以對整機的裝配進行預測，從而保證（zhèng）數控（kòng）機床的加工精度。文中（zhōng）以（yǐ）臥式加（jiā）工中心為例，如圖 1 所示，其幾何精度要求很嚴格，在微米範圍內。考慮到生產的成本（běn），不可能僅通過高水（shuǐ）平的製造能力提升公差要求來確保數控機床的裝配精度。

因此，在實際（jì）機床裝配過程中（zhōng），一般會采用測量和調整的手段來減小誤差。狀態空間模型是一種描述裝（zhuāng）配偏差傳遞的有效方法［4］。

加工中（zhōng）心主要由床身、立（lì）柱、主軸、各種直線導軌和回轉軸（zhóu）組成。其中每一（yī）部分都會由其本身的加工、裝配、運動及發熱等產生誤（wù）差。當一部件（jiàn）沿導軌運動時，將產生 6 個自由度的誤差，這些誤差項通過機床運動的傳遞和變換構成幾何誤差，此，精確地（dì）建立機（jī）床空間誤差十分重要（yào）。目前機床誤差的理論建模技術主要有基於運動學模型、基於多（duō）項式模型等。

在（zài）基於運動學模型的誤差建模技術方麵：D L Leete 等於（yú）1961 年首先利用三角關係建（jiàn）立了三軸機床的幾何誤差模型［5］；Schultschik 於 1977 年（nián）利用矢量表達方法分析三軸（zhóu）銼床的空間誤差分量［6］；Ehmann 等於 1993 年提出了一種直接空間誤差分析法［7］；Kiridena 等用（yòng）機構學方法建（jiàn）立五軸機床的空間誤差模型［8］；Eung-Suk Lee 等於 1998年對三坐標銑床 21 項誤差進行了測量，通過誤（wù）差合成法（fǎ）建立空間誤差模型［9］。

近幾年來也（yě）出現了很多其他建模方法：楊（yáng）建國在 1998 年利用齊（qí）次（cì）矩陣變（biàn）換原理（lǐ）建立了車削加工（gōng）中心的幾何與熱誤差綜合（hé）模型［10 -11 ］；Rahman 等於 2000 年同樣基於齊次坐標矩陣建立了多軸數控機床（chuáng）的準靜態誤差綜合空間誤差模型［12］；Bohez等於（yú） 2011 年以將機床運動部件簡化為剛體為前（qián）提對五軸機床進行了誤差補償［13］。

因此，多軸數控機加工係統的誤差分析和補償問題一直備受國內外專家關注，也（yě）一直是學者們研究（jiū）的熱點（diǎn）。但是目前為止還未有一種（zhǒng）係統性、完整性和（hé）通用性的建模（mó）方法（fǎ）。近幾年，為了解決複雜機械係統的誤（wù）差分析，多體係統理論應運而生。多（duō）體（tǐ）係（xì）統理（lǐ）論可以對複雜的（de）多軸機床進行係統性描述，同（tóng）時能夠（gòu）綜合考慮（lǜ）影響係統的多項因素，因此被廣泛適用於複雜機械係統的建模［14］中。

由床身、立柱、主軸、刀架（jià）、刀具和回轉軸部件（jiàn）等構成的機床，從本質上（shàng）看就是一（yī）個複雜機械係統，因此非常適合采用多體係統理論進行研究。然而，目前大多數的研究依然停留在理論模型的分析（xī）上。文中則從實際機床產品的（de）加工中（zhōng）心出（chū）發，應（yīng）用多體係統理論得到一般機床的精（jīng）度建模方法，並利用這一方法對具（jù）體實例（lì）進行分析，驗（yàn）證了方法的可行性（xìng）

。

2 、多體係統理論

多體係統理論廣泛應（yīng）用於船舶、航空、車輛、通（tōng）用機械等（děng）產品的設計和試驗［15］，它涵蓋建模和求解兩個階（jiē）段，建模階段包括從幾何模（mó）型形成物理模（mó）型（xíng）的物理建模、由（yóu）物理模型形成（chéng）數學模型的數學建模（mó）兩個過程；求解階（jiē）段需（xū）要根據求解（jiě）類型選擇相應的求解器進（jìn）行數值運算和求解。

利用多體係統理論對圖 1 所示的加工中心精（jīng）度進（jìn）行分析，提出了一種符合實際的分析方（fāng）法。這（zhè）種方法采用齊次矩（jǔ）陣來表（biǎo）示（shì）空（kōng）間中點的位置（zhì）和矢量的姿態，用4×4 階齊次方（fāng）陣（傳（chuán）遞矩陣）對（duì）在理想條件下和實（shí）際條件下靜止狀（zhuàng）態時物體間的（de）相對位置和姿態（tài）進行分析；通過方陣之間的運算，使（shǐ）得多體係統的分析變得簡單、清楚，為實現計算機快速（sù）建模提供基礎［16］。

2．1 空間（jiān）物體的位姿描（miáo）述（shù）

任意兩個零件裝配時，都會（huì）在 6 個自由度（dù）方向上產生誤差，這一誤差稱為靜止誤差（chà）。相對（duì）運動時，也會在 6 個自由度方向上（shàng）產生（shēng）誤差，這一誤差稱為運動誤差。以 x 軸方向平動為（wéi）例進行分析，6 項誤差如（rú）圖 2所示。

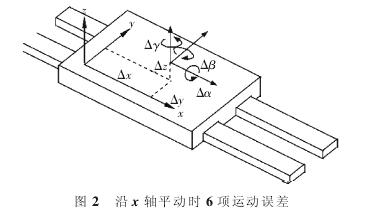
2．1．1 旋轉運動齊次特（tè）征矩陣

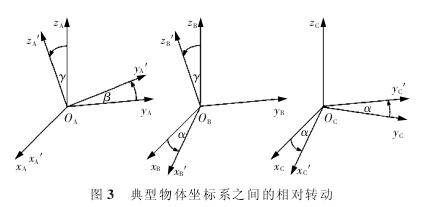
在各種（zhǒng）形式的旋轉運動中（zhōng），把（bǎ）分別繞坐標軸 x，y，z的轉動看成基本轉動，如圖 3 所（suǒ）示，其他複（fù）雜的轉動形式都可（kě）以由這 3 種基（jī）本轉動（dòng）得到。為方便研（yán）究，將複雜的旋轉分解（jiě）到繞坐標軸 x，y，z 的 3 種基本旋轉運動（dòng）來研究。

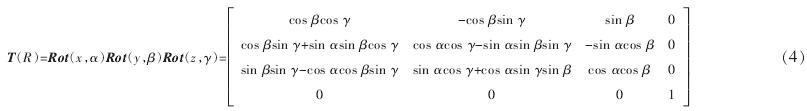
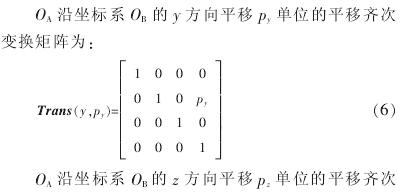
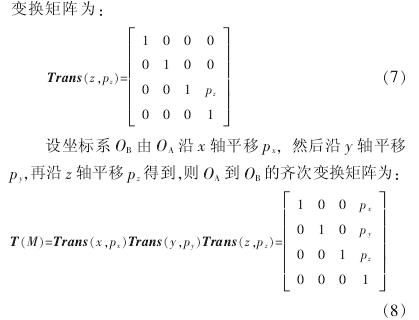
3 、臥式（shì）加工中心精度建模實例

數控機床是一種典型的多體係統，傳統（tǒng）方法顯現了很大的局限性，如需要較嚴格的假設條件，造成分析計算（suàn）結果與客觀事實相（xiàng）差較大。因此（cǐ）用多體係統理論解決數控機床的運動學問題是適用於數控機床研究需求的。文中以第 2 節的理論（lùn）為基礎，根據多軸數控機床（chuáng）的拓撲（pū）結構，利用齊次特征矩陣來對加工中（zhōng）心進行建模。

圖 1 所示（shì）的臥式加工中心（xīn）中，滑枕（zhěn）與滑台的配合（hé）、滑台與床身、立柱的配合實現 3 個方向的運動，使得加工中（zhōng）心有很大的加工範圍。選取（qǔ）產（chǎn）生切削力的軸線（xiàn）方向為 z 軸方（fāng）向，同時規定刀具遠離工件的方向（xiàng）作為 z軸的正（zhèng）方向；x 軸則位於與工件安裝麵相（xiàng）平行的平麵內且垂直與 z 軸，向右為 x 軸的正方向；y 軸與 x 和 z軸垂（chuí）直，向上為 y 軸的（de）正方（fāng）向。

3．1 機床的拓（tuò）撲結構

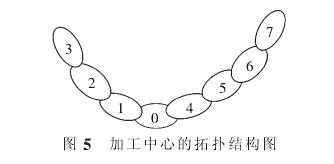
加工中心精度建模的實質是要找到工（gōng）件和刀具（jù）的相對位置。因此從（cóng）臥式加（jiā）工中心的床身出（chū）發，分別沿刀具方向和工件（jiàn）方向建立拓撲（pū）模型。沿工件方向：設床身為 0 號件（jiàn），立柱為 1 號件，滑板為 2 號件，工作台為 3號件（jiàn）；沿刀具的（de）方向（xiàng）：設床身為 0 號件，滑台為 4 號件，滑枕為 5 號件，主軸為 6 號件，刀具為 7 號件。根據（jù）相關拓撲理論［17］，對臥式加工中心的主要零件進行（háng）拓撲，其拓撲結構如圖 5 所示。

3．2 基於裝配的（de）精度模型分析

一般情況下各個零部件之間的裝（zhuāng）配誤差可以通過（guò）實測得出（chū），然（rán）後將誤差數據代入精度模（mó）型中進行分析。文中加工中心的很多因素還在論證和修改階段，因此無法進行裝配實（shí）際數據的提。通過（guò）查閱大量的文獻（xiàn）及（jí）獲取廠方裝配過程所能達到的精度，通過對裝配（pèi）誤差賦值，得到了裝配誤差的一組假設值，並基於此對（duì）精度函數進行計算。假設值如表 1 所示。

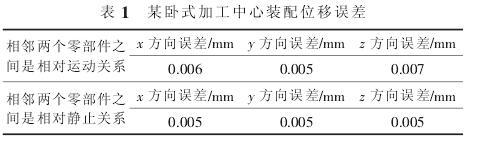
在裝配時，旋（xuán）轉誤差值通常在相（xiàng）對運動的部件間比在相（xiàng）對靜止的部件間大一個數量級。假設值如表 2所示。

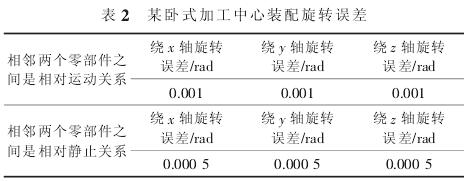
將以上數據進行整理，代到誤差特征矩陣中（zhōng）有：床身（shēn）到立（lì）柱的誤差特征矩陣：

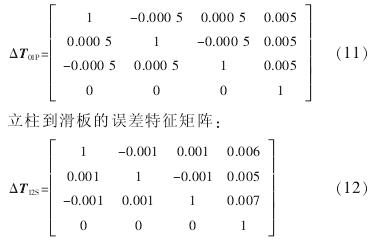
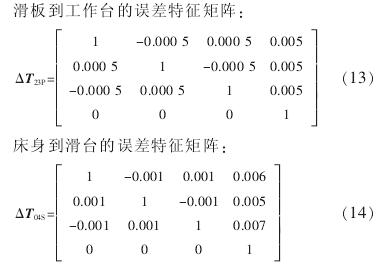
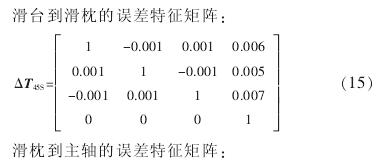
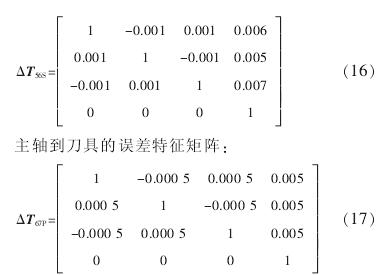
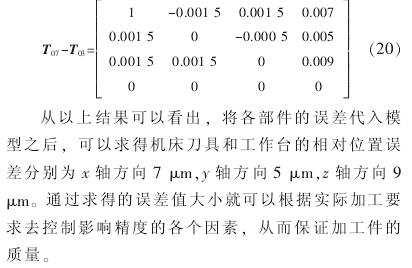
4 、結論（lùn）

首先對多體係統理論進行分析（xī），利（lì）用齊（qí）次（cì）變換矩陣，通過平（píng）移和旋轉後的（de）變（biàn）換矩陣總（zǒng）結出具（jù）有通用性的多軸數控機床精（jīng）度建模方法；再通過對（duì）某臥式加工中心的（de）具體實例進行分析，結合相（xiàng）關文獻及經驗，對（duì）誤差值進行取值並代入建立的誤差模型，計算出刀具與工作台之間的相對位置誤差。這樣可以根據具體的加工要求合理地控製（zhì）關鍵位（wèi）置的相對誤差，為誤差建模提供（gòng）了一種有效的（de）方法。

投稿箱：
如果您有機床行（háng）業、企業相關（guān）新聞稿件發表，或進行資訊合（hé）作，歡迎聯係本網（wǎng）編輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名（míng）企推（tuī）薦

業界視點

| 更（gèng）多

行業數據

| 更多

博文選萃

| 更多