摘要：軋輥（gǔn）磨床磨削過程（chéng）中（zhōng）軋輥表麵經（jīng）常產生振痕等表麵質量缺陷，嚴重製約生產效率和磨削質量． 本文（wén）基於磨床雙時延動力學模型，以砂輪動不平衡為輸（shū）入激勵，建立了軋輥磨床砂輪動不平衡模型，運用龍格--庫塔法進行求解，獲得了砂輪動不平（píng）衡時磨（mó）削係統的動（dòng）力學特性． 通過對正常（cháng）工況與不同砂輪動不平衡量工況的仿真，獲得了其振動響應，並與試驗數據進行對比，驗證（zhèng）了軋輥磨床砂輪動不平衡模型的正確性和（hé）有效性．

      關鍵詞軋輥磨床; 砂輪動不平衡; 磨削顫（chàn）振（zhèn）; 振動特性
  
 
      軋輥磨床是鋼（gāng）材板材軋製生產線（xiàn）的重要配套設（shè）備，由（yóu）床身、砂輪（lún）、頭架、尾架、托架、拖板以及電氣數（shù）控係統等組成，其磨（mó）削精度（dù）和效率（lǜ）直接影響鋼板的軋製質（zhì）量和生產效率． 磨削砂輪動不平衡是磨床磨削過程中常見的故（gù）障，砂（shā）輪動不平（píng）衡進而可能（néng）會（huì）導致磨床顫振，在軋輥表麵形成振紋，影響鋼材的生產效率和質量． 針對這（zhè）一問題（tí），國內外學者進行了一（yī）些研究．

      Inasaki 等詳細（xì）的分析了磨削表麵質量問題，認為再生顫振是產生振痕的主要原因，並通過一係列方法對磨削顫振進（jìn）行過程監測［1］． Yuan 等（děng）建立了輥子磨削過程的時延動力學模型，並利用PD 控製器實現對（duì）砂輪的實時控製［2］． Li 等提出一種時域動力學模型，該模（mó）型考慮了（le）磨入及（jí）磨出時的瞬時顫振現象，進而確定了顫（chàn）振的邊界［3 － 4］． Liu 等提出了雙時（shí）延動力學模型，提出（chū）了（le）一套通（tōng）過控製加工工藝參（cān）數對顫振特性在線監測和控（kòng）製的方法［5］． 一些學者對振痕的監測也做出大量（liàng）工作，Fu 等（děng）通（tōng）過熵函數以（yǐ）及形（xíng）態學分析方法對外圓橫磨（mó）的顫振進行（háng）分類［6］． Oscar 等利用小波變（biàn）換方法對外圓磨件表麵信號進行分析，將顫振信號提取出來並利（lì）用實驗證實［7］． Ahrens 等利用砂（shā）輪處（chù）的力信（xìn）號及振動信號綜合考慮，通過小（xiǎo）波變換等手段對早期顫振進行監測［8］． 國內學者（zhě）也對顫振機（jī）理進行了一定研究，王龍山等基於攝動（dòng）理論和試（shì）驗探討了砂輪與工件接觸剛度非線性對工件顫振頻率的影響［9］． 金滿霞等（děng）分析（xī）了軋輥磨削時的（de）工件係統固有頻率及其對磨削質量的影響，提出（chū）了消除和預（yù）防工件表麵缺陷的方法［10］．綜上所述，目前對磨削顫振的研究主要集中在磨削模型的（de）建（jiàn）立以及磨削顫振特征（zhēng）的識別，以及如何識別這些（xiē）缺陷的特征方麵． 本文針對砂輪動不平衡問題，基於磨削（xuē）雙時延動力學模型，以砂（shā）輪動不平衡力（lì）為輸入激勵，對軋輥磨床磨削過程（chéng）建模，通過與試驗數據對比，驗（yàn）證了模型的正確性，為實（shí）現磨床實時運行（háng）狀態奠定（dìng）了基礎．
 

      1、 砂輪動（dòng）不平衡模型的（de）建立
 
   
      1. 1 軋輥磨床磨削（xuē）過程（chéng）
 
 
      軋輥磨床磨削過程簡（jiǎn）圖如圖1，砂輪寬度為W，質量為mg，旋轉（zhuǎn）角速度為ωg，軋輥兩端由床頭箱及床尾箱頂尖固定，中間由三個拖（tuō）瓦支承，長度為L，質量為mw，旋轉角速度為ωw，且磨削時軋輥隨著拖板左右移動，速度（dù）為V．
   

     
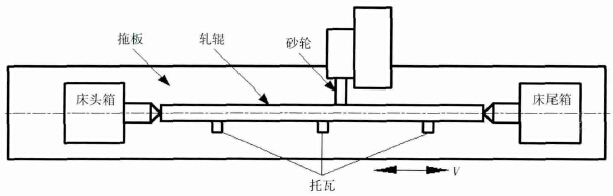
       圖1 軋輥磨床磨削過程簡（jiǎn）圖（tú）
 

      1. 2 軋輥磨床正常模型建立

   
      基於磨削簡圖建（jiàn）立磨削過程動力學模型如圖2，其中KN為砂輪與軋輥的接觸剛度，kg為（wéi）砂輪的支（zhī）撐剛度，c g為砂（shā）輪阻尼，同理kw為軋輥支撐（chēng）剛度，cw為軋輥阻尼，xw為軋輥橫向位移，xg為砂輪橫向位移，mw為軋輥（gǔn）質量，mg為（wéi）砂輪質量，ωw為軋輥轉動速度，ωg為砂輪轉動速度． 建立磨削過程的動力學（xué）方程［5］如下．

     
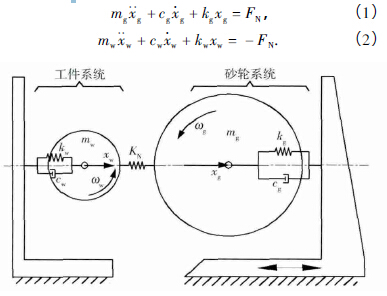
      圖2 軋輥磨床磨削動力學模型

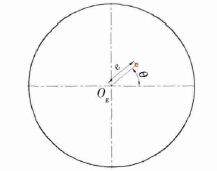
       圖3 砂輪動（dòng）不平衡示意圖
 

      2 、磨削過程（chéng）的仿真分（fèn）析與模型驗證
 
 
      2. 1 磨削過程的仿真
 
 
      本（běn）文（wén）的仿（fǎng）真與試（shì）驗對象是德國某型號重載（zǎi）軋輥磨床（chuáng）． 砂輪質量、軋輥質量、砂輪速度、砂輪寬度、軋輥速度和進給量（liàng）等參數均與現場的實際試驗條件相同，砂輪（lún）阻尼、軋輥阻尼（ní）等為基（jī）於模態（tài）試驗獲取（qǔ），而砂輪剛度、軋輥剛度和接觸剛度為通（tōng）過有限元方法計算得到，具體參數如表1 所（suǒ）示．

      表1 軋輥磨床試驗參數

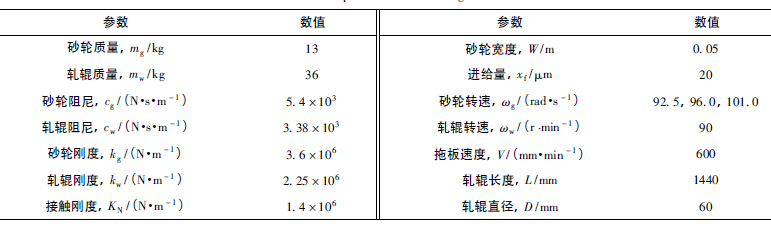
      對（duì）砂輪正常情況與砂輪存在動不平（píng）衡（héng）情況下進（jìn）行仿（fǎng）真分析，結果如圖4．

   
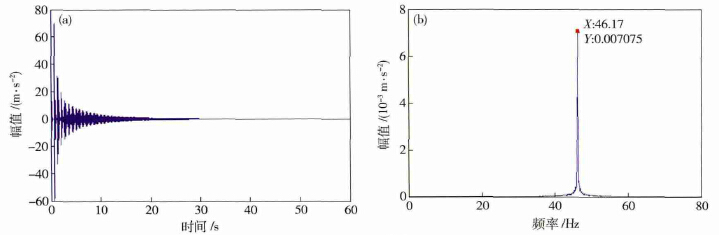
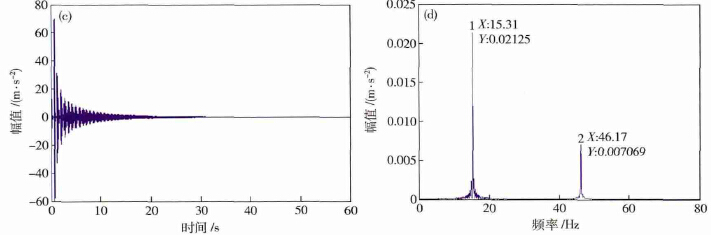
       圖4 動力（lì）學模型仿真結果. ( a) 正常工況響（xiǎng）應時域波形; ( b) 正常工況響應頻域波形; ( c) 砂輪動不平衡工況響應（yīng）時域波形; ( d) 砂（shā）輪動不平衡（héng）工況響應（yīng）頻（pín）域（yù）波形（xíng）

       圖4 中( a) 和( b) 為正常工況響（xiǎng）應，( c) 和( d) 為砂輪動不平衡工況響應． 正常工況與砂輪動不平衡工（gōng）況（kuàng）的仿真時間為60 s，采樣頻率為10240 Hz． 對比正常工況與砂輪動不平衡時域圖，可發（fā）現砂輪存在動不平衡時幅值並未變化，基本一致; 對比正常工況與（yǔ）砂輪動不平衡頻域（yù）圖，可發現砂輪存在（zài）動不（bú）平衡時較正常工況多出15. 31 Hz 的頻率成分，此成分對應砂輪轉頻( 2wgπ － 1 = 15. 31 Hz) ．

   
     2. 2 實驗驗（yàn）證

     現場實驗工況: 床尾頂尖位置（zhì）安裝加速度計，軋輥轉速為90 r·min － 1，砂輪的狀態設置為正常和不（bú）平衡2種工況． 振動傳感器采用ICP 類型，經NI 采集儀器傳輸（shū）調理，獲取（qǔ）振動信號，采樣頻（pín）率為10240 Hz． 采集到的砂輪兩種工況振動信（xìn）號如圖5 所示，( a) 和( b) 為正常工況下振（zhèn）動信號的時域（yù）與頻域分析（xī），( c) 和( d) 為砂輪動不平衡工況下振動信號的時域與頻域（yù）分析圖． 從時域對比可發現發生動不平衡故障時時域幅值（zhí）基本與正常工況（kuàng）相同; 而頻域對（duì）比可看出發生動不平（píng）衡故（gù）障時（shí）15. 31 Hz 處幅值由0. 00485 m·s － 2增加到0. 0106 m·s － 2，該頻率對應（yīng）砂輪的轉頻． 這個結論與模擬（nǐ）仿真的結果一致（zhì）．

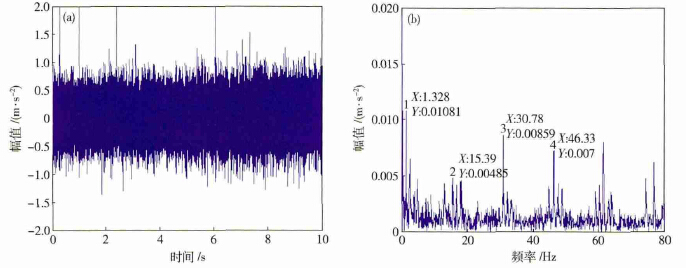
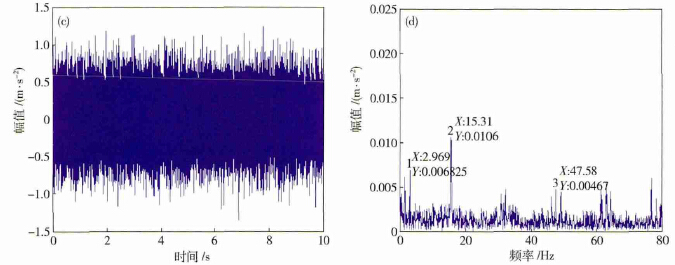
      圖5 實（shí）測數據砂輪（lún）正常工況與（yǔ）動不平衡工況振動響應對比. ( a) 正常工況振動信號時域波形; ( b) 正常工況振動信號頻域波形; ( c) 砂輪動不平衡工況振動信號時域波形; ( d) 砂輪動（dòng）不平衡工況振動（dòng）信號頻域波形

     3 、砂輪不同動不平衡量下磨床振動響（xiǎng）應分析

      為進一（yī）步考察動不平衡量對磨削係統的（de）振（zhèn）動特性的影響，在磨削參數不變的前提下，分別對不同的砂輪動不平衡量、不同砂輪轉速下的振動響應（yīng）進行仿真分析． 德國某型（xíng）重載軋（zhá）輥磨床屬於高精（jīng）度磨床，查找相關（guān）標準知該磨床的砂輪動不平衡許用量［e］＜ 10 μm．故取砂輪故障情況下動不平衡量分（fèn）別為20、40、60、80、100 和120 μm，砂輪的旋轉角速度分（fèn）別為92. 5、96. 0 以及101. 0 rad·s － 1，其對應的砂輪轉動頻率分別（bié）為14. 69、15. 31 以及16. 09 Hz． 磨削係統的振動響應，如圖6 所示．

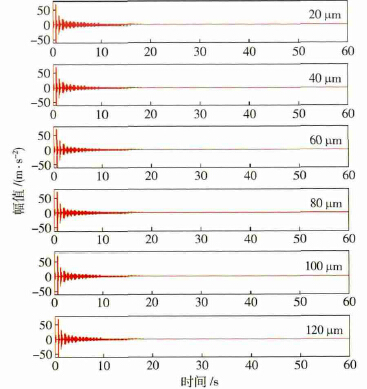
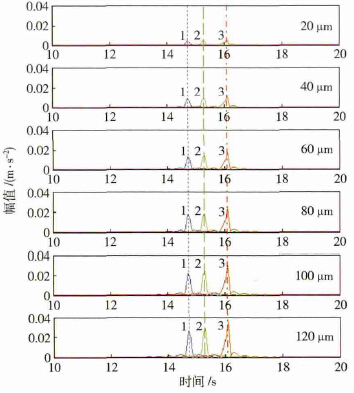
      圖形中“藍線”代表砂（shā）輪（lún）旋轉（zhuǎn）角速度為92. 5 rad·s － 1 下響（xiǎng）應（yīng），“綠線”代表砂輪旋轉角速度為96. 0 rad·s － 1 下響（xiǎng）應，“紅線”代表砂輪旋轉角速（sù）度為101. 0 rad·s － 1 下（xià）響應．

     圖6 砂輪不同動不平衡量以及不同旋轉角速度下的動力學響應． ( a) 時域仿真響應; ( b) 頻域仿真響應
 
 

      圖6( a) 為6 種砂輪（lún）不同動不平衡量以及三種不同旋轉角速度的磨削係統振動（dòng）響應圖． 經對比可發現動不平（píng）衡量在20 μm 到120 μm 範圍（wéi）內，時域上（shàng）幅值不會有太大影響，基本（běn）保持不變（biàn）; 而從不同的三（sān）種旋轉角速度（dù）來（lái）看，角速度（dù）為101. 0 rad·s － 1時幅值略微增大（dà），但（dàn）不明顯． 圖6( b) 為6 中不同動不平衡量（liàng）以及三種（zhǒng）不同角速度下（xià）穩定磨削時段的頻域分析． 經對比（bǐ）可發現隨著動不平衡量由（yóu）20 μm 增大到120 μm 的過程中，圖中所（suǒ）對應的（de）“1”、“2”和“3”特征頻（pín）率成分一（yī）直存（cún）在，分別為14. 69、15. 31 以及16. 09 Hz; 隨著動不平衡量的增大，14. 69 Hz 處幅值（zhí）由0. 004339 m·s － 2 增大到0. 02604 m·s － 2 呈線性增長，15. 31 Hz 處幅值由0. 004725 m·s － 2 增大到0. 02834 m·s － 2 呈線性增（zēng）長，16. 09 Hz 處幅值由0. 005918 m·s － 2 增（zēng）大到0. 0355 m·s － 2呈（chéng）線性增長; 且隨著砂（shā）輪轉速的增加特征頻率所對應的幅值也響（xiǎng）應增大，如圖7 所示．

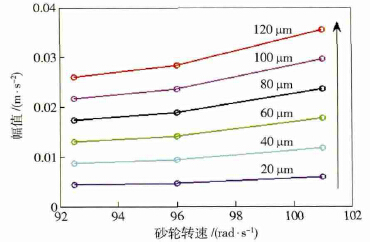
      圖（tú）7 不（bú）同砂輪轉速與動不平衡量特（tè）征頻率（lǜ）幅值趨勢圖（tú）

      4 、結論

     本文建立（lì）了軋輥磨床砂輪動不（bú）平衡雙時延動（dòng）力學模型，通過對仿真數據與（yǔ）實驗數（shù）據的對比分析，驗（yàn）證了模型的正確（què）性和（hé）有效性; 分析了在不同砂輪轉速、不同砂輪動（dòng）不平衡量下，軋輥磨床的振動特征的變化（huà）規律（lǜ）;研究表明軋輥磨床特征頻（pín）率及其幅（fú）值隨著砂（shā）輪轉速以及砂輪動不平衡量的增大而（ér）增大，砂輪轉速越（yuè）高、動不平衡（héng）量越大對磨床的穩定性影（yǐng）響越明（míng）顯（xiǎn）．