摘(zhāi)要:為了預測數控機床運(yùn)行(háng)時熱誤差對進給係統定位精度的影響,以精密(mì)坐標(biāo)鏜床為研究對象,采用紅外熱像儀和激光幹涉儀分別測量進給係統在每(měi)個測點的絲杠溫度和定位(wèi)精度,提出(chū)進給係統熱誤差的最小二乘支持向量機(LS-SVM)預測方法,建(jiàn)立了關於溫度與位置的預測模型。模型引入最小二乘支持向(xiàng)量機方法對機(jī)床進給係(xì)統熱誤差進行預測(cè)分析,較好地描述了進給軸熱誤差與(yǔ)溫度、位置之間(jiān)的非線(xiàn)性關係,且對樣本的依賴度小,有很好的泛化能力,解決了目前(qián)線性擬合模型用特征平均溫度替代(dài)當前測點溫度進行計算而存在較大誤(wù)差(chà)的問題。實驗結果(guǒ)表明,與(yǔ)目前已經在(zài)數控機床上實際應用的線性預測模型相比,LS-SVM 模型對進給係統熱誤(wù)差預測精(jīng)度可達90%,預測精度提高30%以上,取得(dé)了非常好的預測效果,具有較高的現實應用價值。
關鍵詞:進給係統;熱誤差;熱誤(wù)差建模;最(zuì)小二乘支持向量機
目前國產數控機床製造水平(píng)與國(guó)外相比還有一定差距(jù)。其中,國產精密坐標鏜床雖然在一些關(guān)鍵性能指標上(shàng)能接近或達到國外先進水平(píng),但還存在一些國產機床普遍存在的問(wèn)題,如穩定(dìng)性差、可靠性低等。這些問題會隨著機床使用時(shí)間的增(zēng)加(jiā)而變得更加突出,嚴重影(yǐng)響工件的加工質(zhì)量。機床誤差主要包括幾何誤差、熱誤差和切削力誤差等[1],
大量研究表明(míng),熱誤差約占機床總加工誤差的70%[2],且所占比例隨機床精(jīng)密等級不同而有所(suǒ)差異,一般機床(chuáng)加工精度越(yuè)高,熱誤差所占比例越大。機床加工過(guò)程中電機、軸承(chéng)、刀(dāo)具等會產生大量的熱,熱不平衡引起(qǐ)的機床機構變形、定位精度下降,嚴重影響(xiǎng)加工精度,這種由(yóu)熱引起的誤差稱(chēng)為熱誤差。機(jī)床熱誤差的影響因素很多,熱源強度及位置、機械結構、材料(liào)屬性、機床加工環境及加工方式等因素(sù)相互耦合影響機床的溫度場分布及熱誤差,因此機床熱誤差具有非(fēi)線(xiàn)性非穩(wěn)態時變的(de)特性。
研究機(jī)床熱特(tè)性主要是分析機床進給(gěi)係統和主軸係統的熱特性,目前對主軸係統熱誤差預測模型的研究較多,提出(chū)了很多研究方法和熱誤差預測模型,且模(mó)型有很高的預測精度,如時間序列預測模型、BP 神經網絡預測模型、支(zhī)持向量機預測模型(xíng)以及(jí)多元線性回歸預測等,而關於進給軸係統熱誤差研究卻相對較少,熱誤差預測模型簡單、單一(yī)。主要因為進給(gěi)係統熱特性更複雜,實驗中絲杠溫度不易獲取(qǔ),實(shí)驗成本更高等。文獻[3]建立了滾珠絲杠熱誤差的多元回(huí)歸模型。文(wén)獻(xiàn)[4]通過與(yǔ)進給軸(zhóu)平衡安置的石英管求出進給軸的熱膨脹量,間接建立了基於神經網絡(ANN)的位置-熱誤差模型(xíng)。文獻(xiàn)[5]利用激(jī)光幹涉儀對立式加工中心的進給(gěi)係統熱誤差進行了研究,給出了較為(wéi)完整的測試方法。文獻[6]利(lì)用紅外熱像儀對滾珠(zhū)絲杠的溫度場進行(háng)了測(cè)量,並建立了進給軸熱誤差(chà)與關鍵測點溫度的關係模型。文獻[7]利用有(yǒu)限元理論分析機床進給軸係統在不同工況條件下的溫度場分布及熱變形,取得了較為理想的預(yù)測結(jié)果。
本文以精密坐標鏜床為(wéi)研究對象,利(lì)用紅外熱像儀、激光幹涉儀(yí)以及由本課題組自行(háng)研製的溫度采集係統等對(duì)機床進給係統進行同步數據測量。分析了進給係統在不同進給速(sù)度(dù)下的溫度分(fèn)布,研究了坐標(biāo)鏜(táng)床在受熱膨脹下定位精度的變化規律(lǜ)以及影響因素,對進給(gěi)係統熱誤差特征進行了分析,提出進給(gěi)係統熱誤差的最小二乘支持向量機(jī)(LS-SVM)預測方法,建立了關於溫(wēn)度(dù)與位置的(de)預測模型。模型預測結果與目前廣泛應用在數控機床上(shàng)的線性預測模型相比,該模型(xíng)具(jù)有非常好的預測精度和通用性,而且支(zhī)持向量機(jī)是基於統計學習和結構風險最小化原理的方法,其對樣本的依賴度小,有很好的泛化能力,具有非(fēi)常好的現實(shí)應用價值(zhí)。
1 、實(shí)驗設備及測量方法
1.1 實驗對象及測試係統
本文研究對象為昆明機床廠研製的大型精密坐標鏜床,如圖(tú)1 所示(shì)。進給軸X,Y,Z 均為線性同步雙電機驅動,進(jìn)給行程為1200×1000×1000 mm,在20 ℃恒溫車間內機床進給係(xì)統定位精度(dù)為3μm,重複定位精度為1.5 μm,理論最大進給速度F= 64 m/min,實際加工最大進給速度F = 45 m/min。

圖1 精密坐標鏜床
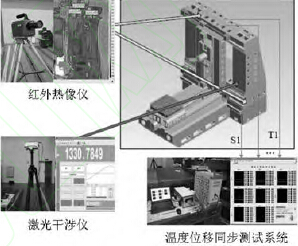
圖2 進給係統熱特性測試係統
測(cè)試係統包括一台雷尼紹公司XL80 激(jī)光幹涉儀,一台FLIR SC7000 紅外熱(rè)像儀及一(yī)套溫(wēn)度位移同步測試係統,測試係統如圖2 所(suǒ)示。激光幹涉儀用來測量機床進給係統的定位誤差,激光幹涉儀補償器可以修正空氣溫度、濕度、壓強等環境因素對測(cè)量精度的影響。紅外熱像儀可以在機床運行時采集絲杠的溫度,並可以直觀的了解熱源對其分(fèn)布的影響。溫(wēn)度位移同步測試係統中利用高精度電渦流傳感器測量絲杠末端受熱膨脹量,記為S1,傳感器(qì)用磁性表座固定在絲杠末端,利(lì)用磁吸式熱電阻溫度傳感器PT100 測量溫度,記為T1-T9。
1.2 測試方法[8-9]
本實(shí)驗是在20℃恒溫實驗室進行的,以X 進(jìn)給軸在不同進給速度下(6、12、18、24 m/min)測量絲杠關鍵點的溫度、絲杠末(mò)端位移和X軸定位精度。進給軸在測量(liàng)範圍[50 mm,1150 mm]內分為12 個測點,如圖3 所示,相鄰(lín)測點相距100 mm,定位誤差的(de)測(cè)量(liàng)方法依(yī)據VDI/ISO 標準,每次測量點停留5 s,每組數據測量3 個往複,設置(zhì)反向越(yuè)程為2mm,消除(chú)反向間隙。開(kāi)機(jī)運行前先冷機測一組數(shù)據作為機床的幾何誤差,便於去除以後數據中的幾何誤差,得(dé)到熱誤差。每組(zǔ)定位誤(wù)差數據測量間隙為30 min,測量時間為10 min,為了減少測量時產生的熱量對測量結果的影響,測量(liàng)時進給速(sù)率降為0.5 m/min。溫(wēn)度數據每5 min 保存一次,溫度測點及位移測點安裝位置如圖4 所示。具體(tǐ)位置如下:(1)上端絲杠部分:電機外殼溫度(T1),前軸承(T6),螺母(T5),後軸承(T7);(2)下端絲杠部分:電機外(wài)殼溫度(T4),前軸承(T9),螺母(T2),後軸承(T8);(3)環境溫(wēn)度(T3);(4)X 軸(zhóu)下端絲杠末端熱伸長量(S1)。測點冷態時的幾何誤差i0 E 為

其中i 為溫度測點(diǎn)編號,j 為測量數(shù)據的組數編號,且(qiě)i = 1,2,…12,測量(liàng)組數 j =1,2,…N,機床在580min時(shí)已經達到熱平衡,對應N =14。
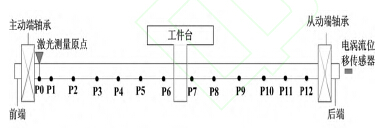
圖3 軸(zhóu)上測點分布示意圖(tú)
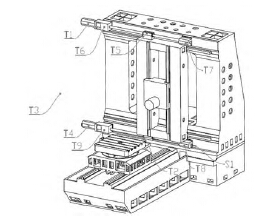
圖4 溫度、位移傳感器安裝位置(zhì)示意圖(tú)

圖 5 紅外熱像儀圖譜(pǔ)
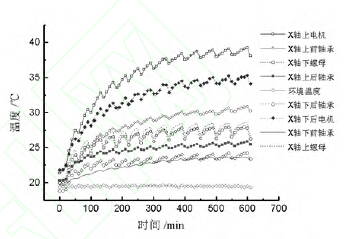
圖6 溫度敏感點溫度值圖
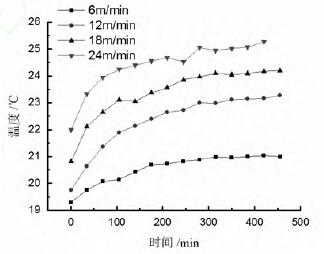
圖7 不同進給速度下絲杠平均溫度
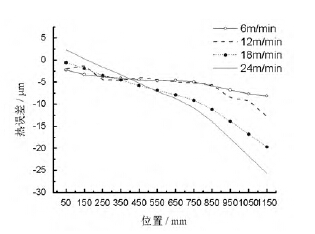
圖8 不(bú)同(tóng)進給速度下穩態(tài)定位誤差
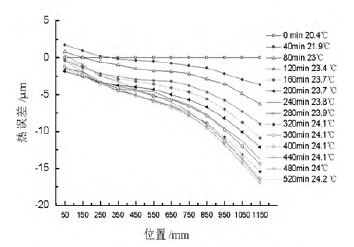
圖9 F=18m/min 進給軸誤差與位(wèi)置和溫度關係圖
2 、實驗結果及分(fèn)析
機床產生熱誤差是由於機床受熱膨脹,結構熱不平衡引起的,熱誤差肯定與溫度有關,由進給軸絲杠受熱膨(péng)脹(zhàng)不均以及定位光柵尺的(de)熱變形引起的機床的定位誤差,在不同(tóng)的坐標位置(zhì)也應該是不一樣的,本次實驗數據也驗證了這一點。圖5 可以直觀了解加工過程中機床溫度及熱源分布情況,溫度越高的地方紅外輻射能量越大,在圖中就顯示的越白(bái)亮,經過處理可以獲得(dé)需要部位的溫度值,通過這種方法獲得絲杠上測點的溫度值。
2.1 機床溫度場(chǎng)分析
溫度位移同步(bù)測試係(xì)統測(cè)得機床進給係統熱敏(mǐn)感點溫度值,如圖6 所(suǒ)示。由圖可知,環境溫度大約(yuē)穩(wěn)定在(zài)20 ℃,X 進給(gěi)軸上電機溫度最高,為(wéi)39.26 ℃,次高(gāo)點是進給軸下電機,為35.3 ℃;本(běn)研究對象精(jīng)密(mì)坐標鏜床進給係統為雙驅結構,電機為進給係統動力源,其產(chǎn)生的熱量(liàng)應該(gāi)是最大的,為最主要熱源,PT100 溫度傳(chuán)感器是磁吸在電(diàn)機外殼上,電機內部溫度應該還高於測量值;雙驅結(jié)構(gòu)在同步(bù)控製和結構(gòu)、製造上的差異導致(zhì)上、下電機溫度(dù)值不同,觀(guān)察其他數據可得,上部(bù)溫度測點值都高於對應的(de)下部溫度測點值(zhí)。距離上電機最近(jìn)的上軸承溫度值約為30.9 ℃,僅低於上下電機溫度,因為電機產生熱量首先通過靠近的軸承(chéng)向外傳導,其次,軸承在運行(háng)過程中也會產生大量的熱。絲(sī)杠後端(duān)的(de)軸承由於遠離主要熱源,溫度(dù)相對較低隻有(yǒu)25.7 ℃。圖中數據(jù)有明顯的周期波動,因為每隔(gé)30min 就要降低進給速度(dù)測量測點的定位精(jīng)度(dù),測量期間產生的熱量減(jiǎn)少溫度值下降,圖中的波動周期也剛好對應這個(gè)時間段。
通(tōng)過式(3)計算絲杠的特征平均溫度,得出在不同進給速度下(xià)絲杠特征平均(jun1)溫度隨時間的變化圖,如圖7 所示。由(yóu)圖7 可知,進給速度越大,絲杠溫
度越高。
2.2 機床熱誤差分析
圖8 是機床在達到熱平衡後,不同進給速度下不同(tóng)測點上的機床熱誤差隨(suí)坐標變化曲線圖。由圖可知,機床達到熱平衡後熱誤差在靠近電機端為正值,遠離電機端為負值,且遠(yuǎn)端誤差絕對值較大,中間各點誤差(chà)隨(suí)坐標近似線性分布。進給速度越大,溫度值越大,熱膨脹引起的熱誤差就越大,圖中數據也驗證這個規律,進給速度越大,誤差越大。以測點1150 mm 處為例,進給速度為6、24 m/min 時,熱誤差分別達到最小值(zhí)和最大值,分別(bié)為-8.2、-25.8 μm。圖9、圖10為進給速度F=18 m/min 時,熱誤差與(yǔ)位置、溫度和時間的關係圖。圖9 中,機床運行時間越長(zhǎng),平均溫度越大,定位誤差越大。從(cóng)圖10 可明顯看出誤差隨著測點坐標增大而增大,在520 min 時,絲杠特征平均溫度為24.2 ℃,測點的整體熱誤(wù)差最大,此時在測點1150 mm 處,熱誤差(chà)最大約為-16.8μm。

圖10 F=18 m/min 進給軸(zhóu)誤差與(yǔ)位置和(hé)時(shí)間關係圖
3 、進給軸熱誤(wù)差建(jiàn)模
清楚了熱誤差的影響因(yīn)素之後(hòu),需要對機(jī)床熱誤差進行建模預測。機床主軸係統熱誤差預測模型研究較多,取得了比較多的成果,而進給軸係統則(zé)相對較少且(qiě)模型(xíng)簡單、預測精(jīng)度不高[10]。目前進給軸係統熱誤差(chà)預測模(mó)型(xíng)多為線性擬合模型(xíng),該預測模型已(yǐ)經在(zài)許多工業(yè)機床數控係統中得到應用,如西門子828D、840D 數(shù)控係統及國產(chǎn)華中數控係(xì)統等,並取得一定的效果,但是該模型簡單預測精度較低[11]。本文引入最小二乘支持向量機模型對機床進給係統熱誤差進行熱(rè)誤差預測分(fèn)析,該模型對樣本的依賴度小,有很好(hǎo)的泛化能(néng)力[12]。通過模型誤差預(yù)測對比(bǐ),支持向量機模型具有更高的預測精度,取得了非常好的(de)預測效果,具有較高的現實應用價(jià)值。以精密坐標鏜床的X 軸為研究對(duì)象,選取進給(gěi)速度F=18 m/min,對進給係統熱誤差進行建模。
3.1 最小二乘支持向量機
支持向量機本質是一個二類分類的優化策略,使分類之間距(jù)離最大化。對於非線性分類問題,通過選取(qǔ)適當的核函數( , ) i K x x 把數(shù)據映射到高維空間,則可以(yǐ)將任意(yì)的數據映射為線性可分,具有非常好的非線性處理能力。Suykens 在(zài)標準SVM 的目標函數中增加了誤差平方和項(xiàng),利(lì)用誤(wù)差平方和作為損失函數,提出了最小二乘支持向量機方法(fǎ),並采用加權的方法(fǎ)成功地解決了模型魯棒性弱以及稀疏(shū)矩性不足的缺陷[13]。 最小二乘法是一種廣泛應用的數學(xué)優(yōu)化方法,在支持向量機預測模型中(zhōng),構建誤差平(píng)方項,尋找滿(mǎn)足誤差平方值最(zuì)小(xiǎo)化的條件,得到(dào)最佳函數匹配。本(běn)支持向量機模型基於結構風險化監督學習策略,目標函數為


根據極值存在條件,拉格朗日函數對各變量的偏導數(shù)滿足一(yī)下條件
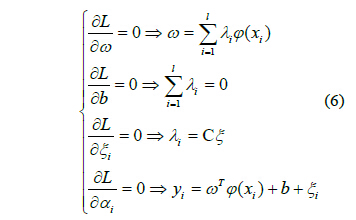


模型輸入為x(P,T),輸出為對應位置、溫度下的熱誤差。P 是測點在絲杠(gàng)上的位置坐標,T 是當前測點對應的絲杠位置上的溫度。由於(yú)熱(rè)誤差影響因素關係比較複雜,為提高模型預測精度,可(kě)以增加

3.3 熱(rè)誤差預測模型比較
線性(xìng)擬合模型[14-16]建模過程本文不再(zài)贅述。圖11 是(shì)溫度值(zhí)為21.9 ℃和24.2 ℃時,兩(liǎng)種(zhǒng)模型熱誤差預測值隨(suí)位置變化曲線圖,圖11 中上麵3 條曲(qǔ)線對應的溫度值是21.9℃,下麵3 條對應溫度值為24.2 ℃。線性擬合模型預測最大誤(wù)差(chà)絕對值在對應溫度(dù)下分別是1.6 μm 和4.43 μm,誤差絕對平均(jun1)值為0.647 μm和2.31 μm,預測精度為51.8%和65.6%,LS-SVM 模型預測最(zuì)大誤差絕對值分別是0.197 μm和0.725 μm,誤(wù)差絕對平均(jun1)值為0.074 μm 和0.259μm,預測(cè)精度高達94.5%和96.1%。圖12 和圖13分別是測(cè)點250 mm 和650 mm 熱誤差隨時間變化曲線圖,線性擬合模型(xíng)預測精(jīng)度(dù)分別為56.46%和(hé)60.8%,LS-SVM 模型預測精度分別為91.68%和93.27%。最小二乘支持向(xiàng)量機模型預測精度明顯高於線性擬合模型。

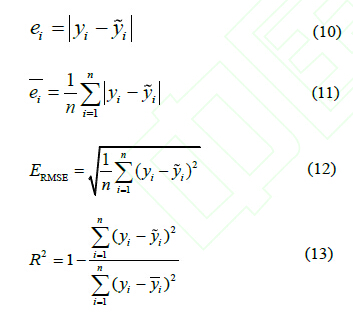

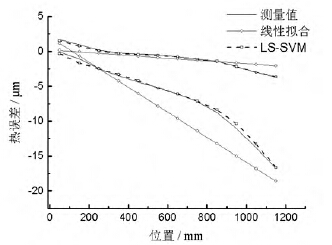
圖11 不同特征平均溫度下預測值隨位(wèi)置變化圖
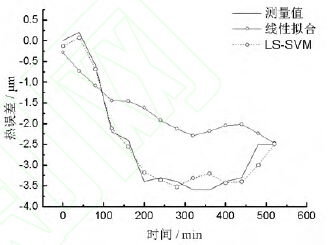
圖12 測點250 mm 熱誤差變化曲線圖
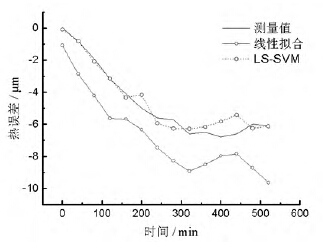
圖(tú)13 測點650 mm 熱誤差變化曲線(xiàn)圖
表 1 誤差預(yù)測模型優劣評價參數

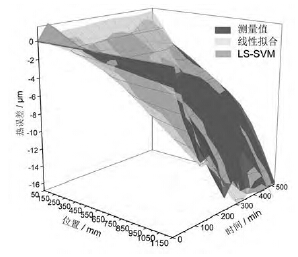
圖14 線性擬合、LS-SVM 模型誤差預測圖
4 、結 論
本文測量了不同(tóng)進給(gěi)速度下進給係統在不同位(wèi)置/溫度下的熱誤差,分析了加工過程中機床產生的(de)熱量對進給軸係統定位精度的影響。以精密(mì)坐標鏜床進給係統X 軸為例,建立了(le)LS-SVM 熱誤差(chà)預測模型,驗證(zhèng)了LS-SVM 模型可以較好的(de)描述進給軸熱誤差與(yǔ)溫度、位置之間的非(fēi)線(xiàn)性關(guān)係。接著可以用相同方法建立進給係統其他軸以及(jí)主軸的預測模型,最後建立整(zhěng)機在不同溫度(dù)和進給坐標下的(de)熱誤差預測模型。
線性擬合模型在熱誤(wù)差計算過程中(zhōng),把同一時刻(kè)下不同位置測點對應的溫度值,統一用絲杠特征平均溫度替(tì)代,而每個測點的熱誤差是由當前位置(zhì)的坐標值和溫度值共同決定的(de),這種近似用特征平均溫度值替代當前測點的溫度(dù)值計算測點熱誤差,無論模型怎麽完善都會存在較大的誤差。支持向量機是基於統計學習和結(jié)構風險最小化原理的方法,對樣本(běn)的依賴度小,有非常強的非線(xiàn)性問題處理能力,通過對比兩種模型熱誤差預測精度,LS-SVM模型具有非常高的預測精度,有較好的應用價值。
如果您有(yǒu)機床行業、企業相關新聞稿件發表(biǎo),或進行資訊合作(zuò),歡(huān)迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
- 2024年11月 金屬切削機床產量數據
- 2024年11月 分地區金屬切削機床產量數據
- 2024年11月 軸承出口情況
- 2024年11月(yuè) 基本型乘用車(轎車)產量數據
- 2024年11月 新能源汽車產量數據
- 2024年11月 新能源汽車銷量情況
- 2024年10月(yuè) 新能源汽車產量數據
- 2024年10月 軸承出口情況(kuàng)
- 2024年10月(yuè) 分地區金屬切削(xuē)機床產量(liàng)數據
- 2024年10月 金屬切削機床產量數據
- 2024年9月 新能(néng)源汽車(chē)銷量情況
- 2024年(nián)8月 新能源汽車產量數據
- 2028年8月 基本型乘用車(轎車)產量數據




