機床關鍵幾何誤差辨識方法研究
2015-1-21 來源(yuán):數控機床市場網 作者:重慶大學 張根保 範秀(xiù)君(jun1)
摘要:在給出機床關鍵幾何誤差和影響因子定義(yì)的基礎上, 提出了識別機床關鍵幾何誤(wù)差的(de)新方法。以一台精密臥式加工中心為例, 利用多(duō)體係統理論建立(lì)了機床幾何誤差與(yǔ)綜(zōng)合誤(wù)差的映射關(guān)係模型, 通過計算和比較影響因子, 最終識別(bié)出 16 項(xiàng)影響機床精度的關鍵幾(jǐ)何誤差。示例表明:該方法可以有效地識別出對機床綜合(hé)空間誤差影響(xiǎng)較大的(de)幾何誤差因素, 從而為合理經濟地進行精度設計和(hé)控製提供重要的理論依據。
關鍵詞:多體係統理論;數控機床; 精度設計; 誤差模型; 影響(xiǎng)因子
0 引言
精度是衡量機床性能的重要指標之一。近年來,隨著市場對(duì)高精度機床需求量的增加,提高機床精度的研究也日(rì)益受到重視。經過國內外學者長期不懈的努力,在誤差(chà)預(yù)防和誤差補償方麵(miàn)均(jun1)取得了長足的(de)進步。利用三角函數關係推導了機床幾何誤差模型(xíng)。提出了基於解析二次型模型的機床廣義誤差模型,並首次在(zài)誤差模型中考(kǎo)慮了熱誤差因素的影響。提出了基於齊次坐(zuò)標變換矩陣的建模方法,該方法可(kě)以對機床的任(rèn)意拓撲結(jié)構進行建模,通用性強、易於程序化,上海交(jiāo)通(tōng)大學、天津大學(xué)、國防科(kē)技大(dà)學等院校應用該方法進行了(le)機床誤差建模和誤差補償研究,取得了可喜的成(chéng)果。機(jī)床的精度最終(zhōng)體現為刀具實際位置與理論位置的偏離程度,受(shòu)到機床各單元體的位置和姿態誤(wù)差的影響。每個單元體的誤差對機床精度的(de)影(yǐng)響程度不同,且在時間維上的變化速率也各不相同(tóng),因此,研究機床幾何誤差對機床精度(dù)的影響程度並加以預(yù)防和控(kòng)製(zhì)對提高機床出廠精度(dù)和(hé)進一步研究精度保持性具有重要(yào)意義。
本文以國家科技重大專項“精密(mì)數控機床精度保持(chí)性技(jì)術研究” 課題(tí)為背景,采用齊(qí)次坐標變換矩陣方(fāng)法建立機床各單元體誤(wù)差與(yǔ)機床精度的映射關係模型,並從中提取出(chū)關鍵幾何誤差項,為實施機(jī)床精度設計與控(kòng)製研究提供依據。該方法同樣適用於其(qí)他類型機床的誤差溯源和關(guān)鍵誤差項的(de)辨識。
1 機床綜合誤差模型(xíng)的建立
1.1 機床的特征矩陣
本文以精密臥式加工中心 TH6380 為研究對象(xiàng),圖 1 為其結構示意圖,主(zhǔ)要由床身、3 個直(zhí)線運動軸 (X、、Z) 和2 個旋轉軸(B、C) 組成。圖(tú)2所示為其相應的拓撲結構(gòu),可將機床分為 2 個支鏈, 即床身 →Z 軸滑板 →B 軸 → 工件;床身 →X軸滑板 →Y 軸滑板 → 主軸 → 刀(dāo)具。
選擇機床原點建立慣性坐標係 B0,依次在(zài) X軸滑塊、Y 軸滑(huá)塊、主軸、刀具、Z 軸滑塊、B 軸(zhóu)上建立運動坐標(biāo)係,分別為 B1、B2、B3、B4、B5、B6、B7,各坐標(biāo)係均為右(yòu)手笛卡爾坐標係(xì)。設某個單元體圖 1 TH6380 結(jié)構示意圖
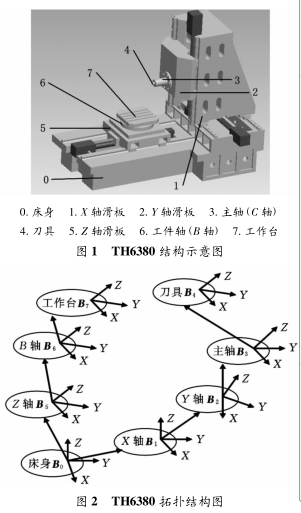
上的坐標係為(wéi) Bk,與(yǔ)其相鄰(lín)的低(dī)序(xù)體(tǐ)的坐標係為Bj,則有
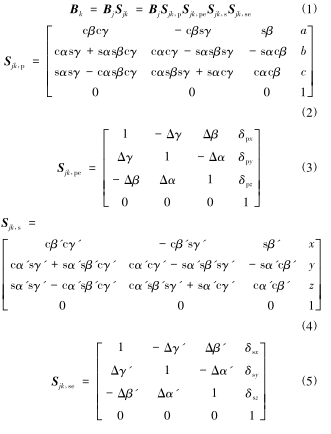
式中,Sjk為相鄰體變換矩陣,描述其單元體 j、k 坐標係間的變換關係;Sjk,p為(wéi)位置變化矩陣(zhèn);Sjk,pe為位置誤差矩陣(zhèn);Sjk,s為位移變換矩陣(zhèn);Sjk,se為位移誤差矩陣;s 表示 sin,c表示 cos;α、β、γ 為位置坐標係的偏角(歐拉(lā)角);α'、β'、γ'為運(yùn)動坐標係的偏角;a、b、c 與 δpx、δpy、δpz分別為 Bk和(hé) Bj間的相對初始位(wèi)置和(hé)位置誤差;x、y、z與δsx、δsy、δsz分別為Bk和 Bj間的相(xiàng)對運動增(zēng)量和運動誤差。
機床的單(dān)元部件一般存(cún)在 6 項基本誤(wù)差。圖3 所示為以 X 軸(zhóu)滑板為例進行的各誤差項及表征符號示意(yì),其誤差包括(kuò) X、Y、Z 方向的(de)線性位移誤差δx(x)、δy(x)、δz(x) 和繞 3 個軸向的旋轉誤差εx(x)、εy(x)、εz(x)。對於高精密機床,則還需要考慮運動副的初始位置(zhì)誤差項(即0 位誤差)。受篇幅所限,本文隻列出了 X 軸滑板的運動狀態(tài)的特(tè)征矩(jǔ)陣。
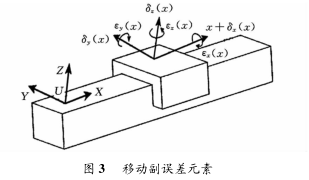
X 軸滑板(bǎn)0 位時的理論(lùn)位置特征矩陣、X 軸滑板 0 位時的位置誤差矩陣、X 軸滑板(bǎn)的理論運動特(tè)征矩陣和(hé) X 軸滑板的運動誤差矩(jǔ)陣可分別表示為式中,x0、y0、z0為 X軸(zhóu)滑板位於0 位(wèi)置(zhì)時,其上的坐標係原(yuán)點在床身固(gù)定坐標係中的坐標;Δx0為 X 軸0 位誤差;x 為(wéi)X 軸滑板的運動位置坐標;δx(x)、δy(x)、δz(x) 與(yǔ) εx(x)、εy(x)、εz(x) 分(fèn)別為 X 軸在 x、y、z 方向上的位移誤(wù)差和角(jiǎo)度誤差。
1.2 THM6380 加工中心綜合誤差(chà)建模
假(jiǎ)定(dìng)刀具切削刃中心點 T 在刀具坐(zuò)標係下的坐標為 QT= (xT,yT,zT,1),在工(gōng)件坐標係下(xià)的理論坐標為 QW= (xW,W,zW,1),實際坐標為Q'W= (x'W,y'W,z'W,1),由機床拓撲結構(圖 2)和式(1) ~ 式(5) 可得(dé)到如下轉換關係:
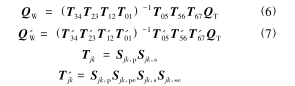
式中,j、k 為 2 個相鄰體的序號。
通過分析式(6) ~ 式(7) 中的參數變量可知,機床的綜合誤差 E 與幾何誤差 G、各運動軸坐標 U、刀(dāo)具坐標係下(xià)的刀具位置坐標(biāo) QT有關(未考慮熱誤差因素),因此,可確定機床(chuáng)的綜合誤差E(刀具的理論位置和(hé)實際位置的偏差值) 與各幾何誤差項的映射關係模型為
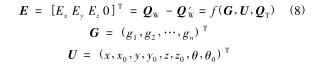
式中,G 為機(jī)床幾何誤差向量(liàng);n 為誤差項數量;U 為運動軸坐標向量(liàng);x、y、z、θ和 x0、y0、z0、θ0分別為 X 軸(zhóu)、Y 軸、Z軸、B 軸的運動坐標和初始位置坐標。
在誤差參數辨識的基礎上可獲取機床(chuáng)各單元的特征矩陣,再將其代入式(8),即可(kě)得到該機床的具體的(de)數學表達式。利用式(8) 不(bú)僅可以建(jiàn)立機床的誤差補償模型,還可以分析各誤(wù)差(chà)項對綜合誤(wù)差的影響,以便合理地進行精度設計和控(kòng)製。
2 機床關鍵幾何誤差的識別
2.1 關鍵幾何(hé)誤(wù)差的定義
機床綜合誤差是幾何(hé)誤差的非線性函數,幾何誤差對綜合誤差的影響亦各不相同,研究幾何誤差對綜合誤差的影響程度對於機床精度設計與控製具有重(chóng)要的意義。聯想到導數的概念(niàn)及涵義,本文將對綜合誤差影響大的幾何誤(wù)差定義為關鍵幾何誤差。由式(6) ~ 式(8) 可(kě)知,E是G、U 的連續可微函(hán)數,E/gi(i = 1,2,…,n) 必存在,並將| E/gi| 定義為影響因子 ki。因此,關鍵幾(jǐ)何誤差項的識別即為比較影響因子ki大小的過程。借用“ 80/20”法則,機床關鍵幾何誤差對綜合誤差的影響(xiǎng)應至少占全部幾何誤差影響的80%,本文給出的識別關鍵幾何誤差(chà)的表達式為
式中,K 為關鍵幾何(hé)誤差的影響(xiǎng)比重;m 為 ki從大到小排序的序號。
2.2 關鍵幾何誤差的識別
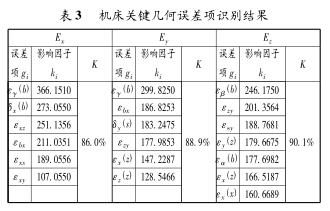
在分析機床(chuáng)結構及其運動關係基礎上,結合GB/T20957.1-2007—《精密加工(gōng)中心檢驗條件》對機床幾何誤差(chà)檢驗項的要求,得到其中主要影響機床加工精(jīng)度的幾何誤差有 36 項,即 n = 36。利用 QC20 -W 球杆儀(yí)和雙頻激光幹涉儀等檢(jiǎn)測工具(jù)對各幾何(hé)誤差(chà)進行檢測,表 1 所示為部分幾何誤差檢測結果。將各運動軸的坐標、刀具坐標和表1 中的幾何誤差代入式(8),即可得到機(jī)床在任意測點位置的誤差值。本文以加工中心常(cháng)用加工區域內一點(x,y,z) = (400,330,210) 為例,進行關鍵幾何誤差項的識別,用於測量(liàng)的測棒(刀具) 坐標(biāo)位置矢量為(wéi) QT= (0,0,-300,1)。表 2僅列出了綜(zōng)合(hé)誤差 E 與幾何誤差 G 的映射(shè)關係(部分)。由式(9) 計(jì)算得到(dào)的影響機床綜合誤差的(de)關鍵(jiàn)幾何誤差結果如(rú)表 3 所示。


2. 3 關鍵幾何誤差的影(yǐng)響分析
由表(biǎo) 3 可以看出(chū):B 軸繞 Z 軸的偏角誤差εγ(b),B 軸在 X 向的徑向跳動 δx(b), X 軸分別與Z 軸、B 軸、Y 軸、主軸 S 的(de)垂直度 εxz、εbx、εxy、εxs,是影響 X 方向綜(zōng)合誤差 Ex的關鍵幾(jǐ)何誤差項,這6 項誤差對 Ex的影響占 86%;B 軸繞 Z 軸的(de)偏角誤差(chà)εγ(b),S軸在Y向的徑向跳動,Y軸與Z軸的垂(chuí)直度εzy,B軸(zhóu)與X軸的垂直度εbx,Z軸繞X軸的偏角誤差 εx(z),Z 軸的滾擺誤差 εz(z) 是影響 Y方向綜合(hé)誤差 Ey的關鍵幾何誤差項,這(zhè) 6 項誤差對 Ey的影響占 88. 9%;B 軸的定(dìng)位誤差 εβ(b),Z軸與Y軸(zhóu)和S 軸與B 軸的垂直度εzy、εsy,Z 軸的(de)偏擺和仰俯誤差(chà) εy(z)、εx(z),B 軸繞 X 軸的偏角誤差 εα(b),X 軸(zhóu)的滾擺誤差 εx(x) 是影響 Z 方向綜合誤差 Ez的關鍵幾何誤差項,這7 項誤差(chà)對 Ez的影響占90. 1%。
表 3 中共有19 條數據,16 項關鍵幾何誤差。
其中,εγ(b)、εzy、εbx各出現(xiàn)2 次,即對綜合(hé)誤差的兩個方向都有影響,是精度設計和控(kòng)製過程首要考慮的誤差(chà)項;B 軸誤差有4 項,Z 軸誤差有4 項,S 軸誤差有1 項,X軸誤差(chà)有1 項,是精度設計和控製(zhì)過程需重點(diǎn)考慮的單元體;垂直度(dù)誤差有 6 項,是需重點控製的單元(yuán)體體間(jiān)誤差。
上述 16 項幾何誤差是影響該機床綜合誤差的主(zhǔ)要因素,企業可以根據自身的技術能力進行精度設計和控製,經濟合理地提(tí)高機床的(de)精度(dù)。
3 結論
(1) 本文利用齊次坐標變換矩陣法建立了精(jīng)密(mì)臥(wò)式(shì)加工中(zhōng)心(xīn)幾何誤差與綜合誤差的映射關係模型。給出了關鍵幾何(hé)誤差和影(yǐng)響因子的定義,在計算和比較影響因子大(dà)小的(de)基礎上,提取(qǔ)出 16項關(guān)鍵幾何(hé)誤差。
(2) 從關鍵誤差的頻次上劃分,B軸繞Z軸的(de)偏角誤差 εγ(b),S 軸在 Y 向的徑向跳動,Y 軸與 Z軸的垂直度εzy,B軸與X軸的垂直度εbx各出現兩次,可見三者分別對綜合誤差的兩(liǎng)個方向有較大(dà)的影響,是需重點控製的誤差項;從單元體角度劃分,B 軸誤差有 4 項,Z 軸誤差有 4 項,是需重(chóng)點控製的單元體。
(3)本文提出(chū)的方法同樣適(shì)用(yòng)於其他類(lèi)型機床的誤差溯(sù)源和關鍵誤差項的辨識,算法易於編程,從而為國內(nèi)機床企業經濟合理地加強精度設(shè)計和控製工作提供了理論依據(jù)。
投稿箱(xiāng):
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯係本(běn)網(wǎng)編(biān)輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯係本(běn)網(wǎng)編(biān)輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息(xī)
業界視點
| 更多
行業數據
| 更多
- 2024年11月 金屬切削機床產量數(shù)據
- 2024年11月 分地(dì)區金屬切(qiē)削機床(chuáng)產(chǎn)量數據
- 2024年11月 軸承出口情況
- 2024年11月 基本型(xíng)乘(chéng)用車(轎車)產量數據
- 2024年11月 新能源汽車產量數據(jù)
- 2024年11月 新能源汽車(chē)銷量情況
- 2024年10月(yuè) 新能源汽車產量數據
- 2024年10月 軸承出口情況
- 2024年10月 分地區金屬切削機床產量數據
- 2024年10月 金屬切削機床產量數據
- 2024年9月 新能源汽車銷量情況(kuàng)
- 2024年8月 新能源汽車產量數據
- 2028年8月 基本(běn)型乘用車(轎車)產量數據





