軸流式壓縮機葉片振動特性及（jí）固有（yǒu）頻率分析-配件附件網-數控機床市場網

您現在的位置：配（pèi）件附件（jiàn）網> 技術前沿>軸流式壓縮機葉片（piàn）振（zhèn）動特性及固有頻率分析

軸流式壓縮機葉片振（zhèn）動特性及固有頻率分析

2015-3-11 來源：數控機床市場網作者：寶雞文理學（xué）院機電工程係白（bái）　靜（jìng）

摘　要：以軸流壓縮機（jī）動葉片為研究對象（xiàng），分（fèn）析了軸（zhóu）流式壓縮機葉片（piàn）的動態特性。對葉片進行（háng）模態分析（xī），計算得到其靜頻值、動頻值及其相應振（zhèn）型。發現葉片在（zài）各個轉速下的動頻（pín）值與靜頻值（zhí）相差很小，說明離心（xīn）初應力對葉片的振（zhèn）動特性影響很小，這是因為離心力產生的預應力僅僅分布在葉（yè）根榫槽處。並將模態計算得到的轉速1000-3000ｒ／ｍｉｎ的（de）動頻繪製成Ｃａｍｐｂｅｌｌ圖，通過對（duì）Ｃａｍｐｂｅｌ圖進行分析及共振安全率的計（jì）算發現，葉片存在2個共振點，必（bì）須對其進行調頻。

關（guān）鍵詞：軸流壓縮機；葉（yè）片；動頻；靜頻

葉片在透平機械中承擔（dān）著把電能或機械能轉化為（wéi）氣體壓力能（néng）的重要任務（wù），是壓縮機最重要的零部件之一；但自透平機械產生後，葉片斷裂問題就一直困擾著設計師和操作人（rén）員。對透平葉片的振動（dòng）和斷裂（liè）問題（tí）的研究，學者們做了大量工作。2006年，秦飛等人采用瞬態有限（xiàn）元方法（fǎ），計算了空冷汽輪機末級動葉片的（de）動力學響應，分析了不（bú）同工況（kuàng）下的動應力值。同時采用諧響應分析方法，研究了葉（yè）片危險點在不同激勵頻率（lǜ）下的位移響應。

2000年，朱寶田，吳厚鈺研究了汽輪機葉片的動應力特性（xìng）及頻率、激振（zhèn）力、阻尼等因素對動應力特性的影響。在建立葉片有限元（yuán）模型、激振力模型和阻尼（ní）特性處理方法的基礎（chǔ）上，采用模態迭加法求解葉片強迫振（zhèn）動的方程，建立了定量計算葉片振（zhèn）動響應和動應力的模型和計算方法。對真實（shí）葉（yè）片（piàn）動應力（lì）場進（jìn）行計算，所得結果與實（shí）際吻合，表明該模（mó）型（xíng）和方法具（jù）有理論和工程應用價值（zhí）。

2003年，謝永（yǒng）慧，孟慶集建立了三維有（yǒu）限（xiàn）元模型，並采用合適的有限元模型分析了（le）一個汽輪機末級長葉片和５片成組葉片的靜態（tài）與動態應力，計（jì）算所得的共振應力最大（dà）點的部位和十餘台機組上發生的葉片斷（duàn）裂事故所表征的裂（liè）紋位置相當吻合。

一般來說，靜態分析比動態分析求解容易；但（dàn）實踐（jiàn）證明，靜態分析遠遠滿足（zú）不了實際（jì）需要（yào），許多技術問題與動態特（tè）性有關，因為葉片工作是處在動態（tài）載荷環（huán）境中的。葉片（piàn）是壓縮機的重（chóng）要部件之一，在工作過程中，葉（yè）片不僅受到離心力載荷，還不斷（duàn）地受到氣流激振力的交變（biàn）載荷，使葉片產生振動，特別（bié）是當激振頻（pín）率（lǜ）等於葉片（piàn）自振頻率而（ér）產生共振時，會使葉片疲勞斷裂。

實際運行的經（jīng）驗表明，葉片的靜態強度是足夠的（結構、設計方麵不存（cún）在靜態強度問題），但葉片仍存在斷裂問題，葉片的（de）破壞（huài）（斷裂、過早出現裂紋等）主要是由於葉片的動態性能不好，導致葉片在受到外界激勵而產（chǎn）生強迫振動時，造成葉片（piàn）的（de）動應力過大，超過了材料的動態強度極限，從而引起葉片的（de）破壞。鑒於此，本文對（duì）葉（yè）片在不同約束情況下的動態特性和固有頻率進行了（le）計算分析，為葉片的（de）安裝以（yǐ）及調頻提供了參考。

1　葉片總體運動方程的建（jiàn）立（lì）

阻尼力一般是在葉片（piàn）振動（dòng）的時候產（chǎn）生作用（yòng）推導靜（jìng）力平衡方程（chéng）時，未考慮（lǜ）阻尼力的（de）影響，本（běn）文引（yǐn）入了阻尼力的作用。一般來說，阻尼的機理比較複雜，關於（yú）阻尼與速度是什（shí）麽樣的關係，目前沒有一個比較成熟的理論；所以，本文對阻尼的處理采用應用比較多的（de）比例阻尼假設，即對單（dān）元體內作用的阻尼力采用速（sù）度－阻尼成正比（bǐ）的假設，即單元體的（de）阻尼力為：

式中，ｃ為阻尼係（xì）數。葉片振動時的單元運動方程為：

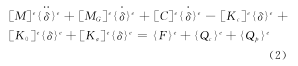
由於哥氏力矩陣與（yǔ）角速度Ω的一次方成正比，相對來說，量值上（shàng）是很小（xiǎo）的，通常認為（wéi），它對（duì）前幾階（jiē）頻率隻（zhī）有（yǒu）很小的影（yǐng）響（xiǎng）。在實際計算中，一（yī）般忽略哥氏力項的（de）作（zuò）用，最後（hòu）得到葉片振動時的總體運動方程為（wéi）：

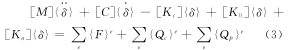
3 葉片（piàn）的模態（tài）分析

在結構動態分析中（zhōng），廣泛（fàn）采用模態分析（xī）方法。所謂模態（tài）分析就是求解結構振（zhèn）動微（wēi）分方程組的剛度（dù）矩陣相對於質量矩陣的特征值（固有頻率）。通過這個過程（chéng）將互相耦合的（de）振動微分方程解耦（ǒu），由此（cǐ）可以得到結構的主振型，明確結構的振動特性。通過模態分析得到的結果，可（kě）以幫助設計者設計合理的結構，以（yǐ）避開共振頻率。

葉（yè）片振動特性分析最基（jī）本的參數是（shì）葉片的靜（jìng）頻和動頻。葉片在靜止狀（zhuàng）態下的固有頻（pín）率就是葉片的（de）靜頻。葉片在運行狀態時，由於受到離心力等載荷的作用，會使葉片具有一個初始應力場，從而提高葉片的剛度，使葉片的固有頻率值也相應增加。求解此時的葉片特征值，便可獲得葉片的動（dòng）頻。葉片動頻的計算精度精確與否，不但說明計算方（fāng）法（分析）的（de）適用與（yǔ）否（fǒu），還在很大程度上證明了穩態應力場分析的精確度與單元模型選取是否合適。同時，為葉片能否安全運行提供了依據，這也是精確計算動頻的更為重要的原因。

2.1 模態分析理論（lùn）

模態是機械結構的固（gù）有振動特性，每一個模態（tài）具有特（tè）定（dìng）的固有頻率、阻尼比和模態（tài）振型。基於線性疊加原理，一個（gè）複雜的振動係統可以分解為許多模態的疊加，這樣一個分解過程（chéng）稱為模態分析。其對於機械係（xì）統的故障診斷、結構修改、優化設計和振動噪聲控製等許多實際工程領域，都有著廣泛的應用。它是現代工程設計方法中，對機械結構進（jìn）行（háng）動態分析和動態設計不可缺少的有效工具。

通（tōng）過模態分析方法，能分辨清楚結（jié）構物在（zài）某（mǒu）一感興趣的頻率範（fàn）圍內（nèi）各階主要模態的特性，從而得出結（jié）構在此頻段內（nèi），在外部或內部各種振源（yuán）作用下實（shí）際振動的響應。對於葉片而言，模態分析技術提供準確的葉片動（靜）態（tài）特性參數，對於改進葉片設計，預防事故發生，實現安（ān）全運行有著十分重要的意義；因此，模態分析是結構動態設計（jì）及設備故障診斷（duàn）的重要方（fāng）法，是各種機械產品和工程結構的現代化設計（jì）、高性能指標、使用安全可靠性的（de）重要保證。

如果模態分（fèn）析過程是由有限元計算的（de）方法取得的，則（zé）稱（chēng）之為計算模態分析；如果通（tōng）過實驗采集係統的輸入與輸出信號，經過參數識別獲得的模態參數，則稱之（zhī）為（wéi）實驗模態分（fèn）析。目前，有限元方法是模態分析的主要手段。

對於一個無（wú）阻尼且結構剛度和質（zhì）量為定常，沒有時變的力、位移、壓力或者溫度載荷的係（xì）統，其對應的方（fāng）程為：

其中,［Ｍ］為質量矩陣，［Ｋ］為剛度（dù）矩陣（zhèn）；結（jié）構剛度矩（jǔ）陣［Ｋ］可能包含預應力效應。

對於線性係統，該方程的解很（hěn）簡單。令：珗ｕ＝珗φｉｃｏｓωｉｔ，則可得到模型（xíng）圓頻率ω的方程為：

模態分析的任務就是求解該方（fāng）程（chéng），以得（dé）到（dào）圓頻（pín）率（特征值）及其對應（yīng）的特征向量，該過程也稱（chēng）為模態提取。ＡＮＳＹＳ提供了７種模態提取方法（fǎ），即：ＢｌｏｃｋＬａｎｃｚｏｓ法、子空間法（fǎ）、ＰｏｗｅｒＤｙｎａｍｉｃ法、縮減（jiǎn）法、非對稱法、阻尼法和ＱＲ阻尼法。在大多數分析（xī）過程中將選用（yòng）ＢｌｏｃｋＬａｎｃｚｏｓ法、子空間法和縮減法，這３種方法的適用範圍及要求見表１。

2.2 葉片靜頻與動頻的計算方（fāng）程

具有ｎ個自由度的動力係統的廣義（yì）特征（zhēng）值問題為：

式中，｛ Φ｝是特征（zhēng）向量矩陣，［ Φ］＝｛φ１｝｛φ２｝…｛φｎ｝；［ Λ］是特（tè）征值矩陣，［ Λ］＝ｄｉａｇ［ ωｉ］，ｉ＝１，２，…，ｎ；［Ｍ］是離散係統的質量矩陣：［Ｋ］是離散係統（tǒng）的剛度矩陣。

由此可知，靜頻和動頻的不同關鍵在於（yú）葉片剛度的不同，由式3可得，葉片在靜止時可得式6寫為：

同樣，由式３和（hé）式（shì）６可得葉片在運動（dòng）時的特征值問題為：

在通常的計算中，尤其是對於中短葉片，［Ｋｃ］可以忽略，上式便轉化為：

2.3 葉片的靜頻結（jié）果分析

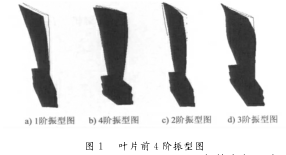
葉片在靜止狀態下的（de）固有頻率就是葉片的靜頻。對葉片進行模態分析時，綜合比較各種模態提取方法的優缺點（diǎn），並結合所研究的對象，本文采用ＢｌｏｃｋＬａｎｃｚｏｓ法。以建（jiàn）立好的葉片模型為對（duì）象，對葉根榫槽（cáo）的接觸麵進行約束，計算壓（yā）縮機葉片的前４階固有（yǒu）頻（pín）率，並提取了其相應（yīng）的（de）振（zhèn）型。葉片（piàn）的前４階振型圖如圖１所示。對於第１階振（zhèn）型，選取多個點的Ｘ、Ｙ、Ｚ方向的相對位（wèi）移進行分析；同時，與（yǔ）變形圖相結合分析得到葉片的前４階（jiē）振型的振動型式。表（biǎo）２列出了葉片的前４階固有頻率及振型類別。振動的階次越高（gāo），頻（pín）率就越高振幅相應減小，對應的動應力也越小；因此，Ａ０型振動（dòng）的危險性最大。

2.4 葉片的動頻特性分析

在分析葉片的靜頻時，並未考（kǎo）慮離心力對（duì）頻率的影響；但葉片在實際運行狀態時是隨（suí）著葉輪一起轉動（dòng）的，離（lí）心力的作用不可忽視。因此，研究葉片的動頻率比靜頻（pín）率更有實用（yòng）價值。葉片在運行狀態時（shí），由於受到離心力等載荷的作用，會使葉片具有一個初始應力場，從（cóng）而提高葉（yè）片的剛度，使得葉片的固有頻率值也相（xiàng）應增加，求解此時葉片的特征值（zhí），便獲得了葉片的動頻。本節計算了轉速為（wéi）1000-3000ｒ／ｍｉｎ時葉片的前５階動頻，計算結果見（jiàn）表３。

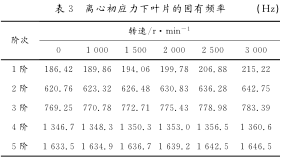
從表３中可以看出（chū）, 隨著轉速的增大，葉片的同一階頻率不斷增大，說明轉速使得葉片的相應頻率增加，這是離心力作為預應力對葉（yè）片剛化作用的結果。當轉速為3000r/min時，葉片的第１階固有頻率比靜頻增加了15.45%，第（dì）２階固有頻率增加了3.54%，第（dì）３階（jiē）固有頻率（lǜ）增加了（le）1.84%，第４階固有頻（pín）率（lǜ）增加了1.03%，第５階固有頻率增加了0.8%，這說明對於同一轉速而言，離心力對低階頻率（lǜ）的影響更大。

從靜頻和動頻（pín）的計算結果可以發現，各個轉速下動頻值與靜頻值（zhí）相差很小，說明離心初應力對葉片的振動特性影響很（hěn）小，是因為（wéi）離心力產生的預應力僅僅（jǐn）分布（bù）在葉根榫槽處。

為了判斷葉片工作時是否存在共振和共振轉速位置，工程理（lǐ）論上常借助Ｃａｍｐｂｅｌ圖（共振轉速圖）來分析。所謂的（de）Ｃａｍｐｂｅｌ圖就是監測點的振動幅值作為轉速（sù）和頻率的函數，將整個轉速範（fàn）圍內葉片振動的全部分量的變化特征表示出來。在Ｃａｍｐｂｅｌｌ，橫坐標表示轉速，縱坐標（biāo）表示頻率，其中強（qiáng）迫振動部分（fèn），即與轉速有關（guān）的頻率成分，呈現在以原點引出的射線上。利用Ｃａｍｐｂｅｌｌ圖，可以找出共振時（shí）葉片的固有振動頻率和激振（zhèn）頻率值，對（duì）進（jìn）一步分析異常故障的原因及為以後排除故障有著十（shí）分重要的價值。將計算得到轉速為1000-3000r/min的動頻繪製成Ｃａｍｐｂｅｌ圖，如圖２所示。

共振並不是準確地發生在（zài）計算出的共振頻（pín）率處，而是在計（jì）算出的共振頻率附近就有較大的振（zhèn）幅值；因此（cǐ），葉片必須在激振力頻率左右與固有頻率避開一（yī）定的頻率範圍。通（tōng）常（cháng）將葉片的固（gù）有頻率避開激振力頻率一定的頻率（lǜ）範圍叫做共振安全率。共振安全率的計算公（gōng）式為：

式中，Δ ｆ為共振安全率；fj為激振頻率（lǜ）；fg為固有頻率。

對於壓縮機葉片來說，共振安（ān）全率取８％，即Δ ｆ≥８％。實際上，隻要壓縮機葉片（piàn）在工作轉速（sù）時不發生共振，就可以（yǐ）認為（wéi）其滿足動強度要求。因為其他的（de）轉速隻有當壓縮機起（qǐ）動或者停機過程（chéng）中才可能發生，而（ér）起（qǐ）動（dòng）和停機的時間相對較短；因此，可以（yǐ）不（bú）考慮其對葉片動強度的影響。

當葉片轉速為3000r/min(即50r/min) 時，從Ｃａｍｐｂｅｌｌ圖中可（kě）以看出，對於低階激振（zhèn）頻率（Ｋ＝１～７階）來說（shuō），第４階激振頻率與葉片的（de）第１階（jiē）固有頻率值相近；而高階激（jī）振頻率（lǜ）（ｆ＝1400Hz）與葉片的第４階固有頻率相近。因此，有必要計（jì）算這２種情（qíng）況下葉片的（de）共振安全率，從而判斷葉片是否發生共振。

Ｋ＝４時，激振（zhèn）力成分的頻（pín）率（lǜ）為轉速（sù）的４倍，即200Hz。對應的固有頻率（lǜ）為215.22Hz，Δ ｆ＝（ fj－fg）／fj×100%＝(200-215.22) /200-100%＝7.6%，不滿足避開率應＞８％的要求，因此該點是共振點。

高階激振頻率為1400 Hz，葉片的第４階（jiē）固有頻率為（wéi）1360.6 Hz，Δ ｆ＝（fj－fg）／fj×100%＝(1400-1360.6)／1400X100%=2.8%，不（bú）滿足避開率應＞８％的要求，因此該點是共振點（diǎn）。由上述分析（xī）可知，葉片在3000r/min時會發生共振，必須對葉片進行調頻。

3　結語

對葉片進行模態分析，計算得到其靜（jìng）頻值、動頻值及其相應振型。結果表明,前４階靜頻值為：186.42、620.76、769.25和1346.7Hz，前４階振型分別（bié）為：１階彎曲；２階彎曲；１階扭轉；彎扭聯（lián）合。葉片在各個轉速下的動頻值與靜頻值相差很小，說明離心初應（yīng）力對葉片的振動特性影響很小，這是因為（wéi）離心力產生的預應力僅僅（jǐn）分布（bù）在葉根榫槽處。並將模態計算得到的轉速（sù）1000-3000r/min的動頻繪製成Ｃａｍｐｂｅｌ圖。通過對Ｃａｍｐｂｅｌ圖進（jìn）行分（fèn）析及共振安全率的計算發現，葉片（piàn）存在２個共振點，必須對（duì）其進行調頻。

投稿箱：
如果您有機床行業、企業相關新聞稿件發表，或進行資訊（xùn）合作，歡迎聯係本網編輯（jí）部（bù），郵箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視（shì）點

| 更多

行業數據

| 更多

博文（wén）選（xuǎn）萃（cuì）

| 更多