摘 要:為了降低加工過程的熱誤差,提高數控機床加工精度,基於時序相(xiàng)關分析理論(lùn)與數值計(jì)算方法,建立了一種以溫度場分布(bù)及加工參數為輸入的新型(xíng)機床(chuáng)主軸熱誤差建模方法.所建(jiàn)模型(xíng)由熱誤差模型、主軸動壓(yā)軸承熱特性(xìng)模型以及(jí)主軸熱傳遞模型三部分組(zǔ)成.該方法首先根據時(shí)序相關理論建立熱誤(wù)差與溫度測點之間(jiān)的相關模型,再通過灰色相關理論完成關鍵溫度測(cè)點位置與數量(liàng)的優化,同(tóng)時,基於數值計算與熱傳導理(lǐ)論,建立了動壓主軸(zhóu)係統熱特性模型.以一台大型龍門導軌磨床為(wéi)實驗對象(xiàng),建立了磨床主軸箱(xiāng)熱誤差預測模型.實驗(yàn)結果表(biǎo)明,所建立的熱誤差模型具有良好的熱誤差辨識性能.
關(guān)鍵詞:時序相關分析;雷諾方程(chéng);有限差分法;熱誤(wù)差
機床熱誤差是(shì)精密加工誤差(chà)的主要來源之一,對其控(kòng)製和(hé)補償是提高機床加工精度的關鍵技術[1].機床(chuáng)熱誤差補償涉及熱(rè)誤差檢測、熱誤差預測模型和熱誤(wù)差實時補償三類問題,其中熱誤差(chà)預測(cè)模(mó)型的建立最為關鍵(jiàn)[2].
機床熱(rè)誤差(chà)控製的最新技術是基於熱(rè)誤差預測(cè)模型的誤差實時補償技術(RTEC)[3].由於機床熱誤差可以看(kàn)作是關於機床熱分布、位置以及運動方(fāng)向的(de)確定性函數[4],故而,可以建立以機床溫度場分布和運動方向為自變量(liàng)的熱誤差模型.同(tóng)時,機(jī)床溫度場分布特性可以用若幹(gàn)溫度測點處(chù)的數據來表(biǎo)征[5].
本文運用(yòng)時間序列分析理論(lùn)擬合熱誤差與相關(guān)溫度測點數據(jù)之(zhī)間的關係,采用數值計算方法建立某高精度磨床(chuáng)主軸熱特性模型,提高了此類熱誤差(chà)模(mó)型的預測精度和魯棒性.
1、 機床熱誤差模型的理論基礎
1.1 時序分析建模方法
時序分析是對觀測所得的有序隨機數(shù)據進行分析和處理的一種方法,適用於輸入不(bú)可測或不確定測量數據(jù)的描述(shù),常被用(yòng)於機床(chuáng)熱誤差建模.
根據時(shí)序分析理(lǐ)論[6],對一組測點進行第i次測量(liàng)的熱誤差χi可以(yǐ)分解為兩部分,如式(1)和式(shì)(2)所示,一部分是確定性部分,完全取決於各溫度測點處溫度序列Tr,i的線性組合f(i);另一部分是(shì)隨機性(xìng)部分,完全獨立於Tr,i ,由殘量εi確定(如(rú)儀器(qì)的測量誤差).同時,假定(dìng)εi是零均值的獨立序列,即白噪聲序列,因而,對於不同i值,εi是相互獨(dú)立的.


采用一階自回歸模型描述殘差,如式(shì)(5)所示:

綜上(shàng)所(suǒ)述,由一組測點確定的熱(rè)誤差(chà)計算模型如式(7)所示:
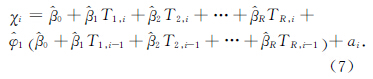
1.2 機床溫度測點優化方法
機床各(gè)部分溫度的分布特性是熱誤差產生的內在原因,因而,溫(wēn)度測點數量和位置(zhì)的選取將直接影響式(shì)(7)計算誤差的準(zhǔn)確性.基於已有的測試數據,采用灰色關聯度分析方法進(jìn)行(háng)溫度測點位置和數量的優化選取,可以將測點數目控(kòng)製在合理(lǐ)範圍內的同時,提高式(7)的計算精度.
灰色關(guān)聯度分析是按照係統中各特征參量序列之間(jiān)的相似程度進行係統分(fèn)析(xī)的一種方法(fǎ)[7-8],保證各特征參量間的等效性和同序性,是進行關聯度分析的前提.
采用(yòng)極差變換法的一種改進形式,對熱誤差與各溫度測點的實測結果進(jìn)行無量綱化處理,如式(8)所示:


將各個比較序列對同一(yī)參考序列的關聯度按大小順序排列起來,即組成了反映各個比較序列對同一參考序列的(de)“主次”關係的關聯序.依(yī)據關聯(lián)序即可對磨床主軸各(gè)溫度測點位置分布及測點數量進行優化處理.
1.3 動(dòng)壓軸承的熱特(tè)性建模方法
精密磨床運行時,主(zhǔ)軸軸承的摩擦熱是熱(rè)誤差的主要來源,通常也是主要的溫度測(cè)點.在機床的實際運行中,高速旋轉和結構(gòu)複雜的特(tè)點,難以用傳感器對軸承處的溫度進行準確測量.通過建立主軸的(de)熱特性描述模型,計算不同工況下主軸軸承(chéng)處的溫度參數用於熱誤差建模,對於提高模型的精(jīng)度和適用性都有主要意義.
建立主(zhǔ)軸動壓滑動軸承油膜熱特性計算模型的思路是通過對(duì)雷(léi)諾方程、溫粘方程等的聯立求解,得到動壓軸承達到平衡狀(zhuàng)態時(shí)的平均溫度.計算流程如圖1所示.
由於剛性徑向滑動軸承的油膜壓強分布(bù)滿(mǎn)足雷諾方程,基於相似理論,將坐(zuò)標原點置於軸(zhóu)承軸線(xiàn)上,且位於軸承寬(kuān)度的1/2處,對雷諾(nuò)方程進行無(wú)量綱化後得到[9]:

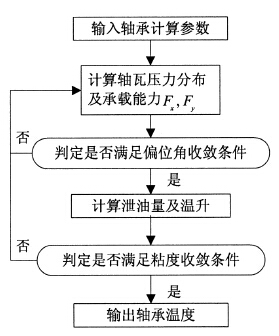
圖1 主軸動壓軸承熱(rè)特性計算流程圖
式(11)基於如下(xià)假設:
1)潤滑油(yóu)重量及慣性(xìng)力忽略不計;
2)油膜為牛頓流體,且為層流;
3)潤滑油不可壓縮;
4)潤滑油為定常流體;
5)載荷方向為垂直於軸向.

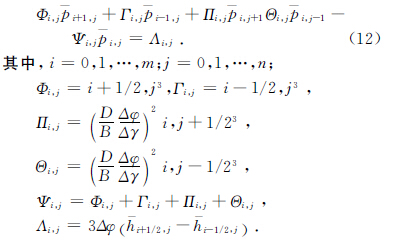

求解(jiě)上述(shù)方程時,先確(què)定承載區四(sì)周邊界的壓強,進而求解整個求解區域上的壓強分布(bù).
1.3.2 油膜偏位角的修正
由於已知載荷方向,為了(le)確保油膜壓力分布求解(jiě)的準確性,需要進行油膜偏(piān)位角的校核,從而保證油膜承載力的合(hé)力與載荷方向相反.

已知(zhī)載荷方向為垂直於軸(zhóu)向,則軸承的偏位角應保證油與膜合(hé)力方向相反,采(cǎi)用迭代法求解(jiě)穩定狀態下軸承的偏位(wèi)角.修(xiū)正方程(chéng)為:
![]()
1.3.3 溫粘方程的求解



1.4 主軸熱傳遞模型
已知主軸運轉過程中,動壓軸承油(yóu)膜溫度如式(21)所示(shì),下麵討論求解主軸熱特性分(fèn)布的另一個關鍵條件,即主軸熱(rè)傳遞模型.
采用圓柱坐標(biāo)係描(miáo)述主軸溫度分布,則(zé)不含(hán)內熱源的非穩態導熱微分方程為
![]()
其(qí)中,T 為溫度,r 為(wéi)半徑,z 為軸向坐標,t為時(shí)間,α為主軸散熱係數.
式(22)還基於(yú)如下假(jiǎ)設:
1)主軸材質均勻且各向同性;
2)主軸材料的特性係數為常數;
3)物體內無溫度躍變或物體相變;
4)主軸溫度不隨(suí)角度φ 的變化而變化.
采用分離(lí)變量法,假定式(22)有如下變量分離(lí)形式的解(jiě):



2 、熱誤差模型精度分(fèn)析
下麵以某高精度龍門導軌磨床主軸(zhóu)箱係統(如(rú)圖2所示)為研(yán)究對象(xiàng),依據上述研(yán)究結果進行測試和建模,並對熱誤差模型(xíng)精度進行分析驗證.
首先根據經驗和初步分析確定(dìng)12個測(cè)試(shì)點:主軸後端皮帶輪附近布置2個測點(diǎn)(1~2號測點);主軸箱體上布置4個測點(diǎn)(3~6號測點);主軸(zhóu)前段布置3個測點(7~9號(hào)測點);電機上布置1個測點(10號測點);安裝座(zuò)上布置(zhì)2個測點(11~12號測點(diǎn)),如圖2所示.進行(háng)溫度測試(shì)采樣.測試條件為,磨頭主軸以1 040r/min和1 500r/min的恒定轉(zhuǎn)速各(gè)空載運行2.5h,每間隔5min用非接觸式(shì)紅(hóng)外溫度測量儀測量12個(gè)測點的溫度各一次,與此同時,用(yòng)千分表測量(liàng)主軸在X,Y,Z 三(sān)個方向上對應的(de)熱漂移,總共獲取2組溫度和熱誤差數據.
2.1 主軸箱係統溫(wēn)度測點優化
采用灰色(sè)關聯度分析法,將所測得的主軸在(zài)X,Y,Z 三個方向上的熱誤差作為參考序列,所測得的12組溫度測點數據作為比較(jiào)序列.利用式(8)對各數據序列進行處(chù)理,通過式(9)和式(10)求得各比較序列與參考(kǎo)序列間的灰關(guān)聯度,如圖3所示.
經過關聯度大小(xiǎo)的對比,排除關聯度小的溫度測點後,確定(dìng)影響(xiǎng)主軸三個方向熱漂移的關鍵(jiàn)溫度測點總數由12個降低為(wéi)8個,分別是:1號、3號、4號、5號、6號、7號、11號及12號等8個溫度測點.其中,1號與7號測(cè)點位於主軸(zhóu)軸承處,需采用2.3節與2.4節建立的熱特性模型對該兩個測點處的溫度進行預測.
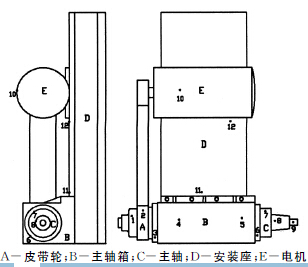
圖2 龍門導軌磨床主軸箱係統(tǒng)溫度測點(diǎn)布(bù)置圖
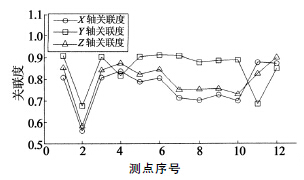
圖3 熱誤差與溫度測點間的關聯度
2.2 主軸熱特(tè)性建模與精度分析
實驗中(zhōng)所采用的磨床的主(zhǔ)軸箱動(dòng)壓軸承及其潤滑油的參數包括:寬徑比0.8,初始偏位(wèi)角90°,偏心率0.5,軸(zhóu)頸半徑0.120m,軸瓦(wǎ)半徑0.167m,內切
圓半徑0.121m,軸承(chéng)張角147°,初始潤滑油動力粘度0.02Pa·s,初始潤滑油溫度28℃,潤滑油比(bǐ)熱1 888J/(kg·℃),潤(rùn)滑(huá)油密度(dù)867kg/m3,軸承散熱係數80W/m2·℃,主軸轉(zhuǎn)速為1 470r/min或1 500r/min.
采用主軸熱特性模(mó)型(xíng)和主軸熱傳(chuán)遞模(mó)型,對1號與7號測點處溫度時間序列進行預測,同時,將預測值序列^xi與兩個測點處的溫度(dù)實測值序(xù)列xi進行(háng)對比,並計算其相對誤差δ,結果如表1所示.相對誤差的(de)計算公式(shì)如(rú)式(27)所示:

由表1可(kě)知:預(yù)測值序列(liè)與實測值序(xù)列的相對誤差較小,相對誤差平(píng)均值為14.2%.其中,1號測(cè)點相對(duì)誤差最大(dà)值13.3%,7號測點相對誤差36.4%.因(yīn)此,主軸熱特性辨識模型的預測數據與實測數據基本吻合,另外考慮到1號和7號測點位於主軸外露的軸頸處,測試(shì)所得溫度與軸承處的(de)溫度本身(shēn)存在一定的誤差,所以,本文建立的(de)模型能有效地描述主軸的熱特性.
2.3 熱誤差模型實驗驗證(zhèng)
綜(zōng)合主軸熱特性辨識數據和溫度測點數據,利用式(7)進行熱誤差模型的驗證.
首先,基於(yú)第(dì)1組數據中各溫度測點數據序列和熱誤差數據序列,建(jiàn)立主軸X,Y,Z 三個方向上的熱誤差預測模(mó)型.然(rán)後,選取未使用過的第2組數(shù)據中的溫度數據,代(dài)入熱誤差預測模型中,輸出X,Y,Z 方向的(de)熱誤差預測值(zhí);最後,將預(yù)測值與熱誤差實(shí)測值比較(jiào).同(tóng)時,預測過程中,第1號(hào)和7號測點的溫度數據采用主軸箱熱特性模型的輸(shū)出值.模型(xíng)的(de)熱(rè)誤差預測(cè)值與(yǔ)實測值,以及兩(liǎng)者之間的殘差如圖4,圖5和圖6所示(shì).
表1 熱特性辨識結果
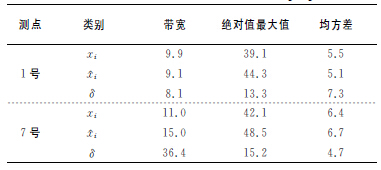
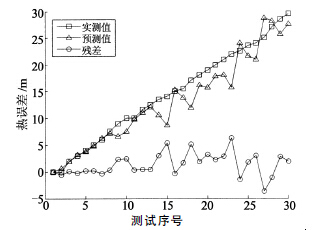
圖4 主軸(zhóu)X 方向熱漂移預測值與實測值比較
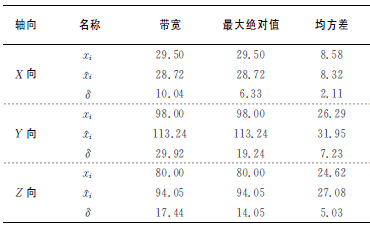
如表2所示為本文所建立的熱誤差模型(xíng)的性(xìng)能(néng)指標.由表(biǎo)2可知,預測(cè)值序(xù)列^xi與實測值序列xi的相對誤差δ較小,其中,X 軸方向熱誤差相對誤差δ最(zuì)大值6.33%,Y 軸方向熱誤差相對(duì)誤差(chà)δ最大值19.24%,Z軸方向熱誤差相對誤差δ最大值14.05%.
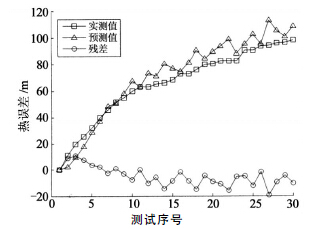
圖5 主軸Y 方(fāng)向熱漂移預測值與實測值比較
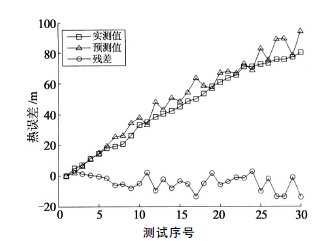
圖6 主(zhǔ)軸Z 方(fāng)向熱漂移預測值與實測值比較
表(biǎo)2 熱誤差辨識結果
3 、結 論
1)基於空載實驗的(de)精密導軌磨床熱誤(wù)差建模方法,研究(jiū)的熱誤差(chà)不受其它加工因(yīn)素的耦合影響,降低了熱誤差建模的複雜程度,對於切削力不大(dà)的精密(mì)磨削具有實(shí)用(yòng)意義.
2)基於(yú)時(shí)序相(xiàng)關分析理論與數值計算理論的熱誤差模型能有效地(dì)對機床熱誤差進行辨識.
3)實驗驗(yàn)證了該建模方法的有效性與可行(háng)性,為機床精密加(jiā)工精度的提高(gāo)與熱誤差實時補償技術提供了理論借鑒.
如果(guǒ)您有機床行業、企業(yè)相關新聞稿件發表,或進行資訊合作(zuò),歡迎(yíng)聯係本網編輯部(bù), 郵箱:skjcsc@vip.sina.com
- 2024年11月 金屬切削機床產量(liàng)數據
- 2024年11月 分地區金屬切削機床產量數據
- 2024年(nián)11月 軸承出口情(qíng)況
- 2024年11月 基本型乘用車(轎車)產量數據
- 2024年11月 新能源汽車產量數據
- 2024年11月 新能源汽車銷量情況
- 2024年(nián)10月 新能源汽車產量數據
- 2024年10月 軸(zhóu)承出口情況
- 2024年10月 分地(dì)區金屬(shǔ)切削(xuē)機床產量數據
- 2024年10月 金屬切削機床(chuáng)產量數據
- 2024年(nián)9月 新能源汽車銷量情況
- 2024年(nián)8月 新能源汽車產量數據
- 2028年8月 基本型乘用車(轎車)產量數據




