主軸集成式光纖光柵切削力測量方（fāng）法研（yán）究-檢驗測量網-數控機床市場網

您現在的位置：檢驗測量網> 技術前沿>主軸（zhóu）集（jí）成（chéng）式光（guāng）纖光柵切削（xuē）力測量方法研究

主軸集成式光纖光柵切削力測量方法研究

2017-3-3 來源：武漢理工大學機電工程（chéng）學院作者：劉明堯，陳功，張（zhāng）誌建，邴俊俊

摘要：為了穩定可靠地測量切（qiē）削加工過程中切削力的（de）大小以對機床（chuáng）的加工狀態進行監測（ＴＣＭ），對基於光纖光柵（ＦＢＧ）傳感技術（shù）的主（zhǔ）軸集成式切削力測量（liàng）方法進（jìn）行了研究。基於光（guāng）纖光柵應變檢測原理和Γ形梁的受力分（fèn）析，提出了４個完全相同（tóng）並且對稱（chēng）的Γ形梁彈性（xìng）體（tǐ）結構；通過對切削力傳遞（dì）規律的分析，建立起（qǐ）了主軸集成式（shì）切（qiē）削力測量理論模型並確定ＦＢＧ的布點；為了驗證模型的（de）準確性，搭建了主（zhǔ）軸集成式光纖光（guāng）柵切削力測量實驗平台，最後通過實驗驗（yàn）證了該方法的（de）可行性和可靠性（xìng）。

關鍵詞：光纖布拉格光柵；主軸集成；切削力；Γ形（xíng）梁

1.引言

切削力是描述切削加工過程中最重要的特征，其大小和動（dòng）態變化反映（yìng）了切削（xuē）過程中刀具與（yǔ）工件的相（xiàng）互（hù）作用情況和工件表麵的形成過程。通過監測（cè）切削加工（gōng）過程中切削力（lì）的變化可以間（jiān）接反映刀（dāo）具切削狀態的變化，因此切削力的精確有（yǒu）效（xiào）測量對於機床加工狀態的監測（ｔｏｏｌｃｏｎｄｉｔｉｏｎｍｏｎｉｔｏｒｉｎｇ，ＴＣＭ）具有重要意義。ＹａｌｄｉｚＳ等人［１２］基於應變片設計了八角環結構的車削和銑削測力儀；ＰａｎｚｅｒａＴ．Ｈ．等人［３］基於（yú）應變片設計出空心圓柱雙端（duān）固定梁結構的車削測力儀；程金生等人［４］基於應變片設計了輪輻型車削力（lì）傳感器；ＲｉｚａｌＭ等（děng）人［５］基於（yú）應變片設計了Γ形梁結構的切（qiē）削力測力儀；而ＳｏｎｇＡ等人［６］基於Γ形（xíng）梁結構設（shè）計（jì）了應變式（shì）多維力傳感器；大（dà）連理工大學的張鐵等人［７］設計出了壓電式車削測（cè）力儀，瑞士的Ｋｉｓｔｌｅｒ公司是壓電（diàn）式測（cè）力傳感器領域的全球引領者，研製出（chū）各種類型的測力裝置，國外的（de）許（xǔ）多學者如ＴｏｔｉｓＧ等人（rén）［８］、ＳｃｉｐｐａＡ等（děng）人（rén）［９］等都使用Ｋｉｓｔｌｅｒ公司（sī）的測（cè）力傳感器在切削力測量領域做了大（dà）量研究；ＪｉｎＷ．Ｌ．等人［１０］和ＡｌｂｒｅｃｈｔＡ等人［１１］利用位移傳感器檢測刀具或主軸（zhóu）的位移來反映切削（xuē）力的大小，並搭建（jiàn）了銑削（xuē）力測（cè）量係統（tǒng）。然而應變片粘貼工藝複雜，處理電路較多，容易受到電磁幹擾；壓電材料對環境溫（wēn）度濕度（dù）要求較高，價格比較昂貴（guì）且本身具有（yǒu）滯後特性；基於位移測量（liàng）的檢（jiǎn）測係統采集的信號幹擾因素多，不能直接反映刀具的工作狀態。劉明堯等人［１２１３］提出基於光纖傳（chuán）感技術的八角環結構切削力測量方法；蔣奇等人［１４］則提出了基於光纖傳感技術的Γ形梁結（jié）構多維力測（cè）量方法，但其都（dōu）是工作（zuò）台式傳（chuán）感器，通過工作台這個媒介間接地測量切削力，工件的大小和質量會對切削力的測量產（chǎn）生影響。光纖光柵傳感技術製（zhì）作的（de）傳感器具有對電絕緣、抗電磁幹擾能（néng）力強、適用於惡劣環境的（de）測量、體積小、能夠在單根（gēn）光纖上實現分布式測量等優點。因此本文基於（yú）光纖光柵傳感技術提出了（le）集成在（zài）機床主軸上的切削力傳感檢測（cè）方法，設計了傳感器結構（gòu），搭建了實驗平台，驗證了主軸集成式光（guāng）纖光柵（shān）切削力測量方法的可行性和可靠性。

２.光纖（xiān）光柵應變檢測（cè）原理

光纖光（guāng）柵反射波的波長同時受反向耦合模有（yǒu）效折射率以及光柵周期影響。它們之間的關係滿足光柵方程［１５］：

而溫度和力都會使光纖光柵的反射波長（zhǎng）發生變化，由（yóu）於本文設（shè）計的傳感器集成在主（zhǔ）軸（zhóu）上，遠離切削加工過程中（zhōng）的熱源，因此認為溫度不變，僅考慮切削力的影響。當光纖光柵受到力（lì）的作用而產生拉伸或壓縮（suō）的時候，光柵周期會發生一（yī）定的變化，同時光纖本身的彈光效應（yīng）會使有效折射率也產（chǎn）生變化（huà）。基於（yú）此，可（kě）以建立（lì）光纖（xiān）光柵的應變傳感模（mó）型如（rú）式（２）所示，它表示了當光纖光柵處於軸（zhóu）向應（yīng）變作用狀態下時（shí），光柵的反射（shè）波（bō）長漂移量（liàng）與軸（zhóu）向應變之間的關係。

出相應測點的應變大小（xiǎo）。

３.轉（zhuǎn）換（huàn）彈性體設計

３．１　Γ形梁受力理論（lùn）分（fèn）析

基於前人對於Γ形梁結構測力傳感器的（de）研究，通過ＦＢＧ傳感技術將（jiāng）其集成在主軸上（shàng）測量切削力（lì）的大小（xiǎo），下麵分析其受力時的應變分布特（tè）征。

主軸上的傳感器（qì）在切削加（jiā）工過程中（zhōng）５個自（zì）由度受（shòu）到限製，隻有沿軸向轉動的自由度，因此僅分析Γ形梁受ＦＸ２、ＦＹ２、ＦＺ２、ＭＸ２和ＭＹ２作用時（shí）的應變分（fèn）布特（tè）點，如圖１所示。

圖１　Γ形梁（liáng）受力示意圖

根據材料力學可（kě）以分別求出（chū）各（gè）個分力作用時ａ、ｂ、ｃ３點（diǎn）的應變值，將他們（men）分別相加即可得到（dào）Γ形梁受力時各個點的（de）總應變大小，如式（５）所（suǒ）示。

３.２轉換彈性體的結構設計

對稱結構受力均勻且便於切（qiē）削力的解耦，因此本文基於Γ形梁的結構設計（jì）了４個完全相同並且對稱的Γ形梁（liáng）彈性體結構，如圖２所示。它包括與主軸相連的中間軸部分、作為彈性元（yuán）件的４個Γ形梁和與（yǔ）刀具相連接的底部圓盤（pán）。

圖２　轉換彈性（xìng）體結構

彈性元（yuán）件的力學特性由其材料和結構決定（dìng），考慮到抗腐蝕性（xìng）、環境因素、剛度（dù）等（děng），本文選用３０４鋼作（zuò）為（wéi）彈性體的（de）材料。

４.切削力傳遞規律和ＦＢＧ布點

４．１切削力傳遞規律

轉換彈性體（tǐ）的結構簡圖如圖３所示，將其４個Γ形梁分（fèn）別記為（wéi）Ⅰ、Ⅱ、Ⅲ、Ⅳ。

圖３　轉換彈性體各梁編號

先定義３個（gè）直角（jiǎo）坐標係：

１）固（gù）定坐標係ＸＹＺ：原點Ｏ為銑刀的刀尖（jiān）點，Ｚ向（xiàng）為主軸（zhóu）的軸向（xiàng），Ｘ和Ｙ向為（wéi）工作台的（de）橫（héng）向和縱向進給方向。

２）旋轉（zhuǎn）坐（zuò）標係Ｘ１Ｙ１Ｚ：原點Ｏ１與Ｏ點重合，Ｘ１方向則（zé）為彈性體梁（liáng）Ⅰ和梁Ⅲ所在方向，Ｙ１方向為彈性體梁Ⅱ和（hé）Ⅳ所在方向。

３）旋轉坐標係Ｘ２Ｙ２Ｚ２：原點Ｏ２為轉換彈性體底部圓盤上表麵的中心，而（ér）Ｘ２、Ｙ２和Ｚ２向分別與Ｘ１、Ｙ１和Ｚ平行。

由圖４中ＸＹＺ與Ｘ１Ｙ１Ｚ的相對位（wèi）置可（kě）以得到（dào）２個坐標係之間的關（guān）係如下：

圖４　固定坐標係ＸＹＺ與旋轉坐標係Ｘ１Ｙ１Ｚ

圖（tú）５　旋轉坐標係（xì）Ｘ１Ｙ１Ｚ與彈性體旋轉坐標Ｘ２Ｙ２Ｚ２

圖６　彈性體受Ｆｘ２、Ｍｙ２作用時變形示意圖

圖６為彈性體受Ｆｘ２和Ｍｙ２作用時（shí）的變形示意圖，其中實線表示變形前，虛線表示變形後的情況。由於梁Ⅰ相對於底部的圓盤（pán）有一（yī）個Ｚ方向的（de）位移，為了抑製（zhì）這一相對運動趨勢，底部圓盤對梁（liáng）Ⅰ還會產生一個Ｚ方向的力，記為ＦＩＺ０。同理，圓盤對（duì）梁Ⅲ也會產生一（yī）個Ｚ方向的力，它們大小（xiǎo）相等，方向相（xiàng）反。故此時梁（liáng）Ⅰ受到３個力的作（zuò）用（yòng）分別為ＦＩＸ、ＦＩＺ０和ＭＩＹ，結合變（biàn）形的協調性，可以得到如（rú）下變形協調方程組：

４．２ＦＢＧ布點

由於光纖（xiān）光柵測量切削力實際上也是感知由切削力在（zài）彈性體（tǐ）上產生的應變（biàn）大小。而應變式力傳感器在布置應變測點時（shí）有應力集中的原則，即將測點布置在應變最大（dà）的地方，由３．１節中的分析可知，應變最（zuì）大的地方都在梁的根部（bù），但是若將光纖光柵粘貼在梁的根部會導致光纖光柵的輸出端光纖產生極大的彎曲從而導致解調儀無法解調出信號。所以，本文布點的原則是在保證解（jiě）調儀能夠解調出（chū）足夠強度信號的前提下，盡量將光纖（xiān）光柵貼到距離梁根部近的（de）地方，並且貼在（zài）各梁表麵寬度的中間處，即中性層上。

具（jù）體的布點及光纖光柵編（biān）號如圖７所示（shì）。本次選（xuǎn）用（yòng）的３根光纖光柵中心波長分別為１５５５ｎｍ、１５５０ｎｍ和１５３７ｎｍ，分別記（jì）為ＦＢＧ１、ＦＢＧ２和ＦＢＧ３。其中ＦＢＧ１粘貼在橫梁的上表麵，ＦＢＧ２粘貼在橫梁（liáng）的側麵，ＦＢＧ３粘貼在（zài）縱梁的表麵，分別對應２．１節中（zhōng）的ａ、ｂ、ｃ３點。

圖（tú）７　光纖光柵的布點及編號

５.實（shí）驗研究（jiū）

５．１　切削力測量實驗平（píng）台

為了（le）通過實驗驗證主軸（zhóu）集成式光纖光柵切削力傳感器數學模型（即式（２２））的正確性以及傳感器的（de）可靠性，本文設計了主軸集成式切削力傳感器實驗平（píng）台。此平台的主（zhǔ）要組（zǔ）成部分如圖８所示。

圖８　主軸集成式光纖光柵切削力測量實驗（yàn）平台（tái）概覽（lǎn）

實際搭建完成的平台如圖９所示。

圖９　測量實驗（yàn）平台實物圖

５．２傳感器的靜態標定

為了分（fèn）析傳感器的可行性和檢測（cè）方法的（de）可靠性，首先需要對傳感器進行靜態標定，即φ＝０°時（shí）傳感器輸入與輸出之間的關係。

５．２．１Ｘ方向切削力的靜（jìng）態標定

平台裝配完（wán）成後，轉動主軸將彈（dàn）性（xìng）體調到初始位置（φ＝０°）。接著（zhe）利用徑向力加載裝置先給彈性體（tǐ）施加上Ｘ方向的切削力，以０．２ｋＮ為步長，直至加到２ｋＮ左右（即依次分別施加０．２ｋＮ、０．４ｋＮ、０．６ｋＮ、０．８ｋＮ、１．０ｋＮ、１．２ｋＮ、１．４ｋＮ、１．６ｋＮ、１．８ｋＮ和（hé）２ｋＮ的力），加載和減載各做３次。將（jiāng）實（shí）驗測得的三個ＦＢＧ的波長數據轉換為應變後（hòu）進行擬合，結果如圖１０～１２。

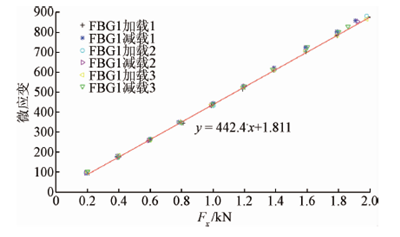
圖（tú）１０　Ｘ方向力加減載時（shí）ＦＢＧ１數據擬合曲線

圖１１　Ｘ方向力加減載時ＦＢＧ２數據擬合曲線

圖１２　Ｘ方向力加減載時ＦＢＧ３數（shù）據擬合曲線（xiàn）

通過對比圖１０～１２可以很直觀地看到（dào）ＦＢＧ２和（hé）ＦＢＧ３的擬合效果不如ＦＢＧ１好，誤（wù）差較大，這是因為受Ｘ方向切削力作用（yòng）時，ＦＢＧ２和ＦＢＧ３處的（de）應變水平與ＦＢＧ１處相比較低，特別是ＦＢＧ２處，滿量程也才９個微應變，而ＦＢＧ１處滿量程有近９００個（gè）微（wēi）應變。因此，Ｘ方向的切削力主（zhǔ）要由ＦＢＧ１來反映。由３條擬合曲線可以得到當Ｘ方向（xiàng）切削力作用時，各個ＦＢＧ產生的微應變大小（xiǎo）規律，即式（shì）（２５）所示。

５．２．２Ｙ方向切削力的（de）靜態標（biāo）定

完成Ｘ方向的加（jiā）減載實驗後，接著進行Ｙ方向切削力的加減載實驗。同理得到當Ｙ方向切削力作用時，各個ＦＢＧ產生的（de）微應變大小（xiǎo）規律，即式（２６）所示。

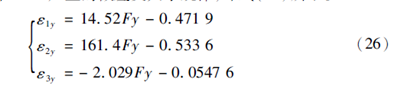
由式（２６）可以看出當彈性體受Ｙ方向切削力作用（yòng）時，ＦＢＧ２的應變水平最高，而ＦＢＧ１和ＦＢＧ３的應變較小，特別是ＦＢＧ３的（de）應變大小相對於ＦＢＧ２來說基（jī）本可以忽略。因（yīn）此，Ｙ方向的切削力主要由ＦＢＧ２來反映（yìng）。

５．２．３Ｚ方向切削力的靜態標定

在完成Ｘ和Ｙ方向的加減載實驗後，最後進行Ｚ方向切削力的標定實驗，同理可以得到式（２７）

可以看出當彈性體受Ｚ方向切削力作用時，３個（gè）ＦＢＧ處的應變水平並沒有如Ｘ和Ｙ方（fāng）向切削力作用時那麽顯（xiǎn）著的區別，因此，Ｚ方（fāng）向切削力測量（liàng）的準確性也是最差的。

結合式（２５）～（２７）可以得到：

由於實際使用時需要根據測（cè）得的應變（biàn）反求處切削力的大小，因此需要通過矩陣運（yùn）算將式（２８）的等號左邊（biān）變為切削力矩陣，經過ＭＡＴＬＡＢ運算後，保留４位有效數字，得到的結果如式（２９）所示（shì）。

式（２９）隻是φ＝０°時的切削（xuē）力模型，還不是完整的數學模型，要（yào）想（xiǎng）得到完整的切削力模型，還需要將轉角矩陣代入其中。結（jié）合式（２２）得到完整的切削力模型如式（３０）所示。

５．３其他角度下傳（chuán）感器的靜態實驗

為了驗證式（３０）在φ≠０°時的適用性，還分別進行了φ＝３０°和φ＝４５°時的靜態試驗。首先以φ＝３０°為例，將初始狀（zhuàng）態下的轉換彈性體轉過３０°，依次分別給Ｘ、Ｙ、Ｚ方向加上１０００Ｎ的切（qiē）削（xuē）力，分別記下３個狀態下３個ＦＢＧ的波長數據。將其轉化為微應變後如表１所示。

表１　φ＝３０°時ＦＢＧ微應變大小

將φ＝３０°，ＦＸ＝０．９９ｋＮ時各個ＦＢＧ微應變大小代入式（３０）的模型中，算得ＦＸ＝０．９６６９ｋＮ，誤差為２．３％，同理可（kě）求得ＦＹ＝１．０４４ｋＮ，誤差為３．４％，ＦＺ＝１．０８５ｋＮ，誤差為７．４％。

再將（jiāng）彈性體調到φ＝４５°的（de）狀態，同樣的實驗過程得到表（biǎo）２。

表２　φ＝４５°時ＦＢＧ微應變大小

此狀（zhuàng）態下算得ＦＸ＝０．９６０６ｋＮ，誤差為４．９％，ＦＹ＝１．０５７ｋＮ，誤差為（wéi）４．７％，ＦＺ＝０．９３２０ｋＮ，誤差（chà）為７．７％。考慮到實驗過程中標定（dìng）時力傳感器的誤差、角度測（cè）量的誤差、光纖光柵粘貼的位置和（hé）質量好壞以及室（shì）溫的波動等影響，根據上述（shù）實（shí）驗（yàn）結果和誤差可以認（rèn）為主軸集（jí）成式光纖光柵的切（qiē）削力測量方法在靜態時是可行的，式（３０）的理論（lùn）模型在靜態時是可靠的。

５．４動態實驗

驗證了靜態時切削力模型的（de）正確性，為了驗證其在動態時（shí）也是適（shì）用的（de），本文（wén）還在（zài）實驗平台上完成了主軸集成式光纖光柵（shān）切削力傳感器的動態實驗。由於還未安裝角（jiǎo）度傳感器，為（wéi）了驗證切削力模型在動（dòng）態時的正確性（xìng），本文將不同主軸（zhóu）轉速、不同切削（xuē）力作用下ＦＢＧ的波長數據進行對比，驗證其是否滿足切削力（lì）模型。

５．３．１徑向力動態實驗

首先將式（３０）做變換，將ＦＹ＝０、ＦＺ＝０代入式中得到（dào）３個ＦＢＧ應變大小（xiǎo）與ＦＸ和主軸（zhóu）轉角（jiǎo）之間的（de）關係如式（３１）所示。

由式（３３）可（kě）以看出，當主軸勻速轉動且切削分力ＦＸ單獨作用時，３個ＦＢＧ的應變（或波長）大小隨著時間呈正弦函數（shù）變化，且其幅值大小與轉速無關，而與力ＦＸ的大小（xiǎo）成正比，轉速（sù）ｎ則影響正弦函數的周（zhōu）期。

１）相同轉速，不同徑向（xiàng）力（lì）

首先將主軸轉速（sù）調（diào）到２００ｒ／ｍｉｎ，並且給彈性體加上１０００Ｎ的（de）Ｘ方向切削力，得（dé）到３個ＦＢＧ波長數據隨時間變化的關係如圖１３所示：

圖１３　ｎ＝２００ｒ／ｍｉｎ，ＦＸ＝１ｋＮ時３個ＦＢＧ波長隨時（shí）間變化

由圖（tú）１３可（kě）以看出，３個ＦＢＧ的波長數據均呈正弦函數（shù）變化，且周期相同（tóng）。保持轉速不變進行ＦＸ＝５００Ｎ、１５００Ｎ的實驗，將３次實驗ＦＢＧ１的數據作對比，如圖１４所示。

圖１４　ｎ＝２００ｒ／ｍｉｎ，ＦＸ＝０．５ｋＮ、１ｋＮ、１．５ｋＮ時ＦＢＧ１的（de）波長（zhǎng）

由圖１４可以（yǐ）看出，相（xiàng）同轉速，不同ＦＸ作用下ＦＢＧ１的波長均呈正弦函數變（biàn）化，且周期相同，但幅值不同，ＦＸ＝１ｋＮ時的幅值為ＦＸ＝０．５ｋＮ時的２倍，而ＦＸ＝１．５ｋＮ時的幅值（zhí）為ＦＸ＝０．５ｋＮ時的３倍，ＦＢＧ２和ＦＢＧ３的規律和ＦＢＧ１相（xiàng）同，由此可知ＦＢＧ的應變大小和ＦＸ成正比，滿足式（３３）。２）不同轉速，相（xiàng）同徑向力將ＦＸ設定為１ｋＮ，再分別進行ｎ＝１００ｒ／ｍｉｎ和ｎ＝３００ｒ／ｍｉｎ的實驗，測得的ＦＢＧ１的波長數據如圖１５所示。

圖１５　ＦＸ＝１ｋＮ，ｎ＝１００ｒ／ｍｉｎ、２００ｒ／ｍｉｎ、３００ｒ／ｍｉｎ時ＦＢＧ１的波長（zhǎng）

由圖１５可以看出，不同轉速，相同ＦＸ作用下ＦＢＧ１的波（bō）長同（tóng）樣呈正弦函數變化，但與相同（tóng）轉速不同ＦＸ情況下不同的是，ＦＢＧ在不同轉速條件下的幅值基本相同，而周期不同（tóng），其中ｎ＝２００ｒ／ｍｉｎ時的周期為（wéi）ｎ＝１００ｒ／ｍｉｎ時的１／２，ｎ＝３００ｒ／ｍｉｎ時的周期為ｎ＝１００ｒ／ｍｉｎ時的１／３，ＦＢＧ２和ＦＢＧ３的規律也和ＦＢＧ１相同，即周期大小與力無關，而與轉速成反比（bǐ）。顯然，這也（yě）滿足式（３３）的規律。

由上述分析可知，徑向力的（de）動態實驗中，ＦＢＧ的應變規律滿（mǎn）足切削力模型。由於ＦＸ和ＦＹ都是徑向力，它們的規律完（wán）全相同，因此可以認為在不同（tóng）徑向力作用下的動態實驗中，ＦＢＧ的應變規律滿足切削力模型。

５．４．２軸（zhóu）向力動態實驗

將ＦＸ＝０、ＦＹ＝０代入式（３０）中得到３個ＦＢＧ應變大小與ＦＺ之間的關係如式（３４）所示。

由式（３４）可以看出，當切削（xuē）分力（lì）ＦＺ單獨作用時，３個ＦＢＧ的應（yīng）變（或（huò）波長）大（dà）小與轉速（sù）和時（shí）間無關，隻與ＦＺ大小成正比，下麵通過實驗驗證其是否（fǒu）正確。將主軸ｎ轉速設置為２００ｒ／ｍｉｎ，力ＦＺ設置為１ｋＮ，得（dé）到３個ＦＢＧ波長隨時間變化的曲線如圖１６所示。

圖１６　ｎ＝２００ｒ／ｍｉｎ，ＦＺ＝１ｋＮ時３個ＦＢＧ波長

從圖１６可以看出，３個ＦＢＧ的波長並不是完全沒有變化的，而是呈現一定周期性，似乎不符合切削力模型。然而這是由於動態實驗中有幹擾的原因，特別是動態切削過程中主軸的軸向跳動使得軸向加載套筒與力加載器之間的接觸壓力發生變化從而使加上的力ＦＺ並不是恒定不變的，通過觀察力傳感器（qì）的（de）讀數，ＦＺ的變化範圍約為０．２ｋＮ，以ＦＢＧ１為例，其可（kě）以引起ＦＢＧ１產生１６．５ με的波動；再就是由於臥式安裝，裝置自身重力會對結果造成幹擾，將簡化模（mó）型導入ＡＮＳＹＳＷｏｒｋｂｅｎｃｈ中進行仿真，可以得到由於自重在ＦＢＧ１上引起的誤差在１０ με以上，且這２個誤差都是隨著主軸轉動呈周期性（xìng）變化的，也就是（shì）說（shuō）各（gè）項誤（wù）差源產生的實驗總誤差在２６．５ με以上。而（ér）圖（tú）１６中ＦＢＧ１的最大波長與最小波長（zhǎng）之間的差值為４０ｐｍ左右，對應微應變（biàn）大小為３３．２ με，然後由（yóu）式（３４）可知由（yóu）１ｋＮ的ＦＺ在ＦＢＧ１處引起的應變大約為８２．４ με，大於３３．２ με，由此可見，圖１６中的波長不（bú）是直線的原（yuán）因並不是切（qiē）削力模型錯誤，而是由於實驗過程中（zhōng）的（de）上述誤差的存在（zài）而導（dǎo）致的，ＦＢＧ２和ＦＢＧ３也（yě）是如此。因此，去除這（zhè）些誤差因素（sù）後，可以認（rèn）為（wéi）在軸向力（lì）動態實驗中（zhōng），ＦＢＧ的應變（biàn）規律（lǜ）基本滿足切削力模型。根據徑向力動態實驗和軸向力動態（tài）實驗（yàn）可以認為切削（xuē）力模型在動態時也是適用的。

６.結論

以切削力為研究對（duì）象，針（zhēn）對傳統（tǒng）應變式和壓電式測力傳感器易受電（diàn）磁幹擾和（hé）平台類傳感器易（yì）受工件質量和大小影（yǐng）響等問題，基於光纖傳感技術提出了集成（chéng）在主軸中的光纖（xiān）光柵傳感器。從理論上分析了切削力的傳遞規律和（hé）受切削（xuē）力作用時彈性體的應變分布規律，建（jiàn）立了切削力測量的理論模型。並搭建了主軸集成式切（qiē）削力傳感器實驗平台以進行實驗分析。通（tōng）過對理論分析和靜（jìng）、動態實驗分（fèn）析的對比，驗證了（le）該檢測方法的可行（háng）性和可靠性。

投稿箱：
如果您有機床行業、企業相（xiàng）關新聞稿件發表，或進行資訊合作，歡（huān）迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視點（diǎn）

| 更多

行業數據

| 更多

博文選萃

| 更多

數（shù）控（kòng）機床（chuáng）