Kalman 濾波（bō）在刀具磨損預測模型中（zhōng）的應用-刀具網-數控機床市場網

您現在的位置：刀具網> 技術前（qián）沿>Kalman 濾波在刀具（jù）磨損（sǔn）預測模型中的應用

Kalman 濾波在刀具磨損預測模（mó）型中的應用（yòng）

2014-2-17 來源：數控機（jī）床市場網作者：張（zhāng）海豔（yàn）, 張臣, 張吉林

摘要: 基於LS-SVM建立刀具磨損預測（cè）模型, 描述銑削過程中輸（shū）入向量(進給率、切削（xuē）速度、主軸轉速、切削深度、切（qiē）削時間及磨損（sǔn）位置) 和輸（shū）出向量(刀具（jù）磨損)之間（jiān）的映（yìng）射關係, 並引入Kalman濾波技術, 建立LS-K F模型, 考慮加工條件及環境變化引起的刀具磨損量的變化, 結（jié）合刀具的實際磨損（sǔn）量更新LS-SVM的預測（cè）結果,並用該更新結果調整訓（xùn）練（liàn）模型, 以使更新後的刀具磨損量能夠反映出由於（yú）加工條件及環境的變化引起的刀具（jù）磨損的變化, 提（tí）高LS-S VM模型的預測精度, 最後用實（shí）驗驗證所（suǒ）建立模型的預測精度。結果表明（míng）, LS-SVM模型和LS-KF模型的預測（cè）精（jīng）度均較高, 且LS-KF模型的（de）預測精度更高。

關鍵詞: 銑削; 刀（dāo）具磨損; LS-SVM; Kalman濾波

隨著航空製造業的高速發展, 對產品精度（dù）、表麵質量、生產效率（lǜ）等有著越來越高的要求, 而刀具磨損對切削過（guò）程中的產品精度、表麵質量及生產效率有著（zhe）重要的影（yǐng）響, 因此成為高標準加工中必須要研究的一個課題。嚴重（chóng）的刀具（jù）磨損可能會導致（zhì）切削震顫, 造（zào）成機器的損壞及刀具和工件（jiàn）的報廢等問題, 因此刀具磨損在任何加工中都應該被控製在加工誤（wù）差的允許範圍內。這個誤差範圍（wéi）的（de）控（kòng）製可以通過建立合適（shì）的（de）刀具磨損（sǔn）預測模型來實現。近年來, 國內外許多學者對刀具磨損都有一定的研究。Wang等[1]提出了基於最優切削元素的預測數學模型, 使用回歸和遺傳算法尋找最優元素, 以預（yù）測高速銑（xǐ）削中的表麵粗糙度。Palani-samy等[2]建立了銑削（xuē）刀具磨損預測的回歸模型和人工神經網絡模型, 實驗結果（guǒ）表明基於人工神經網絡的刀具磨損預測模型在訓練範圍內能夠更好地預測刀具（jù）磨損量（liàng）。Prakash等（děng）[3]對高速鋼及硬質合金鋼刀（dāo）具在車削複（fù）合材料柱體時（shí）的磨損情（qíng）況進行研（yán）究, 討論了切（qiē）削（xuē）條件(切削速度、進給（gěi）率、切削深度)對刀具磨損及產品表（biǎo）麵粗糙（cāo）度的影響。Gajate等[4]分析了直推式學習過程, 建立了模（mó）糊神經（jīng）推理（lǐ）係統用於車削過程中的刀具磨損（sǔn）模型,對每一個有爭議的係（xì）統輸入元素創建一個不同的係統（tǒng）。Li[5]建（jiàn）立了（le）一個新的基於（yú）隱形馬爾科夫算法的刀具磨損預測（cè）模型。Zhang等[6]基於（yú）形狀複（fù）製法建立了球頭刀具磨損預（yù）測模型。

Mahardhi-ka等[7]建立了基於混合動態（tài）模（mó）糊神經（jīng）網絡以及遺傳算法演化模糊神經網絡的球頭銑刀刀具預測模型。本文基（jī）於LS-SVM建立球頭銑刀刀具磨損預測模型, 並（bìng）用Kalman濾波技術更新預測結果, 用更新後的預測結果調整LS-SVM的訓練模型（xíng）, 以期獲得更高的刀具磨損預測（cè）精度。

1 模型（xíng）的建立

1. 1 基於LS-SVM的刀具磨損預（yù）測模型

最小二乘支持向量機[8]是支（zhī）持向量機的一種改進, 它將（jiāng）傳統支持向量機中的不等式約束改為等式約束, 把求（qiú）解（jiě）二次規劃問題轉化為求解線性方程組問題, 以提高求解問題的（de）速度和收斂精度。

LS-SVM的主要公式推導過程如下:

給定N個訓練樣本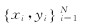

, 其中xi∈RP為P維的（de）訓練樣本輸入（rù）向量,yi∈R是一維（wéi）的訓練樣（yàng）本輸出向量。構造函數y=f(x)表述輸出向量yi對輸入向量xi的映射關係。該方程是以xi作為預（yù）測刀具磨損的輸入參數而yi作為相應的刀具磨損建立的。LS-SVM模型的公式為（wéi）

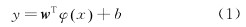約束條件（jiàn）為

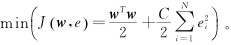。式（shì）中:w為權矢量矩陣（zhèn）; b為偏置量;φ(·) 為將數據映射到（dào）更高（gāo）維特征空間的非線性（xìng）函數; C為正則（zé）化參數; e為隨機誤差。

通過一係列的（de）簡化後, LS-SVM函數的估計表達式為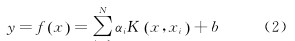

式中: αi為拉（lā）格朗日乘子, αi∈R;K(x, x)i為RBF核函數。

要建立刀具磨損預測模型, 首先需要分析確定影響刀具磨損的特征參量, 如（rú）刀（dāo）具切削參數、切削時間等。本文主要考慮加工參數對刀具磨損的影響, 根據不同（tóng）的加工參數及切削時間預測刀具磨損, 然（rán）後對實驗得到的樣本數據進行預處理, 構建學習樣（yàng）本, 選擇（zé）核函數, 用學習（xí）樣本訓（xùn）練基於LS-SVM的刀（dāo）具磨損預測模型。經過（guò）訓練的（de）LS-SVM模型建立了（le）輸入與輸出元素之間的（de）映（yìng）射關係（xì）, 最後將新的特征量輸入到訓練好的刀具預測模型中, 基於LS-SVM的刀具磨損預測模型, 根據已存（cún）在的映射關係, 對新的特征量（liàng）進行分析運算得到一個輸出結果, 該結果即是基於LS-SVM的刀具磨損預測模型的預測值（zhí）。

基（jī）於LS-SVM的刀具磨損預測模型中需要注意的問題如下:

(1) 樣本數據的歸一化。在機（jī）器學習的應用中, 最重要的一（yī）個問題就是（shì）需要事（shì）先將（jiāng）所有能用到的樣本數據歸（guī）一化（huà）, 即將數據放大或（huò）縮小到某一區間, 使所（suǒ）有不同取值範圍的特征量占有相同的權值比（bǐ）重。同時數據的歸一（yī）化可以減少網絡（luò）訓練時間, 提高網絡收斂速度。

(2) 核函數的選擇。核（hé）函數的選擇決定（dìng）了輸入空間到特（tè）征空間（jiān）的映（yìng）射方式。在LS-SVM常（cháng）用的（de）核函數中, RBF核函數的參數選擇容易, 當參數在有效（xiào）範圍內改變時, 空間複雜度變化小, 易於實現, 並且RBF核函數的應用範（fàn）圍最廣, 直觀反映了兩個數據的距離。鑒於（yú）上述優點, 本文的模型（xíng）中選擇RBF核函數: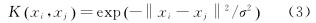

式中: σ為核參數。

(3) 優化參（cān）數的（de）選擇。正則化參數C和核函數（shù）σ在很大程度上決定了（le）LS-SVM模型的（de）學習能力和泛化能力, 其值在模（mó）型建立前是未（wèi）知的, 隻能（néng）在模型運行過程中獲得。為（wéi）了得（dé）到一個（gè）高性能（néng）、高學習效率的LS-SVM模（mó）型, C和σ必須要調（diào）整到最優。本（běn）文中使用網格搜索技術調整兩個參數, 應用交叉驗證（zhèng）和網格搜索法訓練數據得到兩個參數的最優組合。

1. 2 基於LS-KF的刀具磨損預測模（mó）型

Kalman濾波[9]是由狀態方程和觀測方程組成的線性隨機係統的狀態空間模（mó）型來（lái）描述濾波器, 實質（zhì）是（shì）一種最（zuì）優估計方法, 所以適用於刀具磨損狀態的預測。Kalman濾（lǜ）波算法的核心是（shì）Kal-man濾波（bō）遞推方程, 算法主要過程如下:

用xk表示刀（dāo）具從加工時刻0到加工時刻t的磨損量（liàng）( 係統狀態), zk表示刀具從加工時（shí）刻0到（dào）加工時刻t的觀測（cè）磨損量(觀測值（zhí）), uk表示刀具從加工（gōng）時刻t到加工時刻t+1的磨損量, 則刀具磨損量的Kalman濾波公式為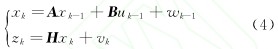

式中: A為係統矩陣, 即狀態轉移矩陣; B為控製向量輸入矩陣; H為測量係數矩陣; wk-1為係統隨機過程噪聲（shēng）序列; vk為係統隨機觀測噪聲序列。

本文設定A、B、H均取為單位矩（jǔ）陣E, 狀態轉移過程輸入噪聲wk-1與測（cè）量噪聲（shēng）vk是不相關（guān）、均值為0、協方差分（fèn）別為Q和R的（de）獨立高斯白噪聲。

Kalman濾波算法的計算流程如圖1所示。

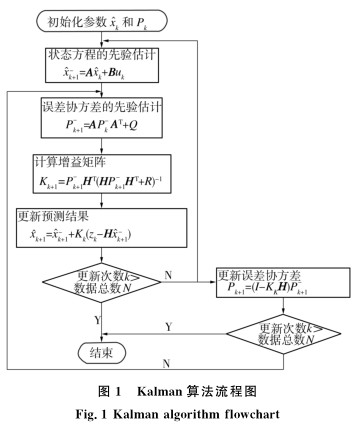
基於LS-SVM的刀具磨損預測模型雖然可以預（yù）測刀具磨（mó）損, 但當刀具（jù）的加工（gōng）條件及環境等因素發（fā）生變（biàn）化時, 其預測出的刀具磨損量並不能很（hěn）好地反映出變化的情況。引入Kalman濾波,結合當時的實際刀（dāo）具磨（mó）損量調整LS-SVM模型的預測結果, 這樣調整後的刀具磨損（sǔn）量就能夠反映出由於加工條件及環境的變化引起的刀具（jù）磨損的變化（huà）。用調整後的刀具磨損量更新LS-SVM模型後再（zài）進行下一步的刀（dāo）具磨損量的預測, 這樣（yàng）下一步的預測結果就能（néng）夠反映出（chū）加工條件及環境的變化。

LS-KF刀具磨損預測模型的結構（gòu）如圖2所示。圖2中, Yp為LS-SVM模型在T+1時（shí）刻的（de）預測結（jié）果,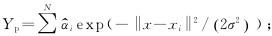

Ym為T+1時刻刀具磨損量的測量值; Yf是利用Kalman濾波技術結合刀具的（de）實際磨損量Ym更新LS-SVM模型預（yù）測結果（guǒ）後的融合數據, 即:Yf=Yp+Kk(Ym -HY)p; Ye是LS-KF模型預測的刀具磨損（sǔn）量。

Ym為T+1時（shí）刻刀（dāo）具磨（mó）損量的測量（liàng）值; Yf是利用Kalman濾波技術結合刀具的實際磨損量Ym更新LS-SVM模（mó）型預測結果後的（de）融合（hé）數據, 即:Yf=Yp+Kk(Ym -HY)p; Ye是LS-KF模型預測的刀具磨損量。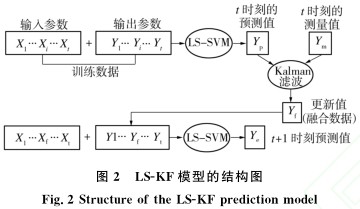

LS-KF刀具磨損預測（cè）模型是基於LS-SVM模（mó）型建立的。LS-KF模型中（zhōng）引入Kalman濾波技術結合當前實際的刀具磨損量Ym來更新（xīn）基於（yú）LS-SVM的磨損預測模型的預測結果Yp。若調整後的誤差小於調整前（qián）的, 則用（yòng）更新後的刀具磨損量Yf調整LS-SVM模（mó）型, 即修（xiū）改LS-SVM的訓練樣本, 若調整後的誤差大於調整前（qián）的, 那麽（me）該次就不進行模型（xíng）的調整, 這樣就會使得模（mó）型的預

測精度進一步提高。

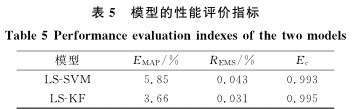
1. 3 模型的性（xìng）能評（píng）價函（hán）數

LS-SVM模型和LS-KF模型的（de）性（xìng）能可以通過實（shí）驗來驗證（zhèng）。為了對模型的（de）預測精度有一（yī）個直（zhí）觀（guān）的（de）評（píng）價, 本文用下麵的幾個（gè）誤差評價函數來分析模型的預測值與（yǔ）真實值之間的關係:

(1) 平均絕對誤差。平均絕對誤（wù）差是所有單（dān）個觀測值與算術平均（jun1）值的偏差的絕對值的平均,是一個用（yòng）來衡量預（yù）測值和測（cè）量值之間偏（piān）離的量,結（jié）果越小表示實際（jì）值（zhí）和預測值（zhí）越接近。其計算公式為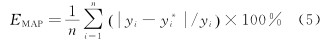

式中: yi為刀具磨損的測量值; y*i 為刀具磨損的預測（cè）值; n為驗（yàn）證樣本的長度。

(2) 均方根誤差。均方根誤差（chà）是（shì）用來衡量預測值和實際（jì）值之間的偏（piān）離程度, 結果越小表示實際值和預測值偏離（lí）越小。其計算公式為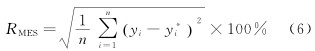

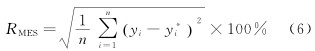
(3) 均等（děng）係數。均（jun1）等係數是用（yòng）來擬合刀具的預測磨損量和測量值之間的關（guān）係, 通常均（jun1）等（děng）係數的值小於1, 且其值越接近1表明（míng）預（yù）測值和實際值的擬合度越好。其計算公式為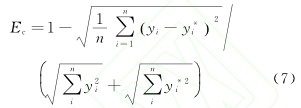

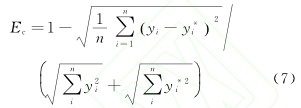
2 實驗

2. 1 模型的訓（xùn）練

銑削加工實驗使用整體式硬質合金雙螺旋（xuán）刃球頭（tóu）立銑刀在加工中心(MIKRONUCP710) 上銑削難（nán）加工材料0Cr17Ni12Mo2不鏽（xiù）鋼工（gōng）件，刀具直徑為12mm, 最大螺旋角30°,幹切削, 切（qiē）削行距為7mm。實驗裝置（zhì）(見圖3) 包（bāo）含一（yī）個有著遠心鏡頭和可調（diào）光源的CCD相機, 相機的另一頭連接安裝了刀具（jù）磨損監測係統的計算機, 用來獲得每次走刀後磨損的刀具圖片。

為了建立刀具磨損模型, 應盡量全麵地考慮（lǜ）影響刀具磨損的因素, 主要包（bāo）括主（zhǔ）軸轉速n、切削深度ap、進給速（sù）度Vf和切削長度L等。采用多因素正（zhèng）交實驗方法, 每個（gè）因素選擇3個水平（píng）, 設計正交實驗獲得不同因素水（shuǐ）平下刀具（jù）的（de）磨損量數據, 用於（yú）訓練模型。正交（jiāo）因素水平表如表1所示。

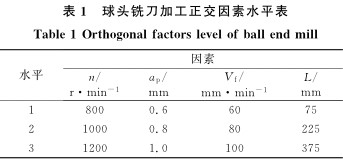
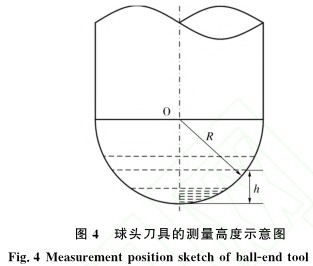
圖4所示為球頭（tóu）銑刀的測量高度示意圖（tú）。用垂直刀具（jù）主軸的平麵把刀具沿高（gāo）度方向分為若幹段 , 每段間隔0.1mm。按表1參數進（jìn）行正交實驗, 利用正交實驗中獲得的刀具磨損（sǔn）圖片可以（yǐ）測得（dé）銑刀（dāo）球（qiú）頭不同高度h處的（de）實際磨損量VB[10],

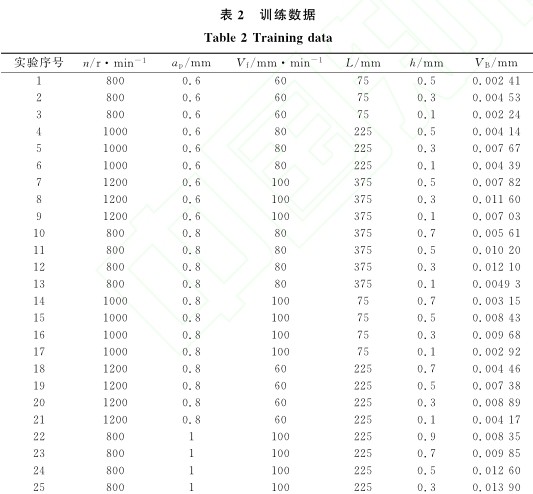
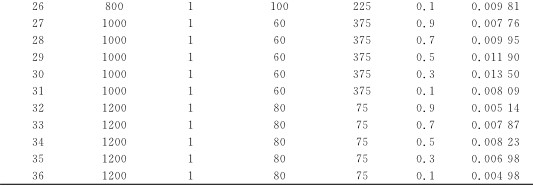
從（cóng）實驗結果中（zhōng）選取表2所（suǒ）示的（de）加工參數訓練（liàn）已建立的（de）刀具磨損模型。訓練（liàn）過程在LS-SVM lab1.5 Tool box中進行, 得（dé）到最好的參（cān）數（shù）組合為C=13.23、σ=14.75。從表2中可以（yǐ）看出, 每次輸入模型的訓練樣本基本都會有小的（de）變動, 也（yě）就（jiù）是所建立的刀（dāo）具磨損預（yù）測模型有微小變化。為了簡化計算且（qiě）保證模型的（de）精度, 用（yòng）表2中數（shù）據訓練模型得到的最佳參數組合C=13. 23、σ=14.75作為這兩個參數後續尋優的網格中心, 以C=12.250∶0.492∶14.218,σ=10.912∶0.443∶12.684為網格進行後續（xù）最佳參數的搜索, 得（dé）到訓練樣本不同時兩個參數的（de）最佳組合。

2. 2 模型的驗證

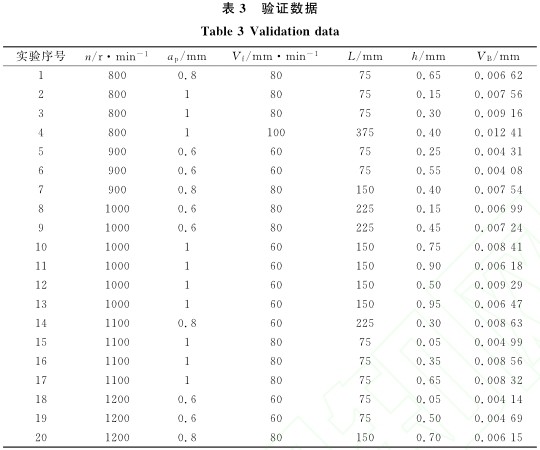
為驗（yàn）證所建刀具磨損預測模型的可靠性, 設計驗證實驗對模型（xíng）的預測結果進行驗證。為了保證驗證精（jīng）度, 驗證實驗數據在表1所示參數最大值和最（zuì）小值的範圍內選擇。實驗及測量方法同正交實驗, 高度（dù）h的間隔為0.05mm。選（xuǎn）擇20組比較合理的測量結果, 如表3所示。用表3中的數據對已建立模型的可靠性進行驗證。

3 兩種模型預測精度比（bǐ）較（jiào）分（fèn）別將LS-SVM模型和LS-KF模型預測的刀具磨損量與（yǔ）實測值進行比較, 得出（chū）兩個模（mó）型的預測誤差如表4所（suǒ）示。由表4可知, 兩組模型的預測磨損量均（jun1）與實際磨損量具有高度的一致性,預測結果與實測值的（de）相對誤差（chà）均在10%以內, 表明（míng）兩個模型的預測精度均較高。

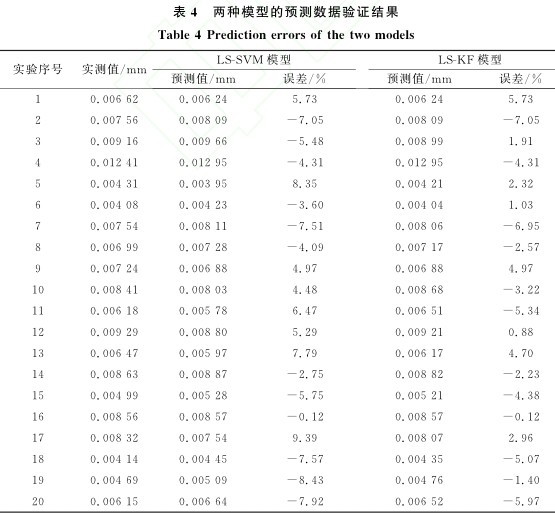
表5所示為兩個模型的性（xìng）能評價指標。從表5中可以看出, LS-KF模型的平均絕對誤差（chà）值小於LS-SVM模型的平均（jun1）絕對誤差值, LS-KF模型的均方根誤（wù）差小於LS-SVM模型的均方（fāng）根誤差, LS-SVM模型（xíng）的均等係數大於LS-SVM模型的均等係數, 表明LS-KF模型的預測磨損量更接近刀具的（de）實際磨損（sǔn）量, 其擬合度更高。

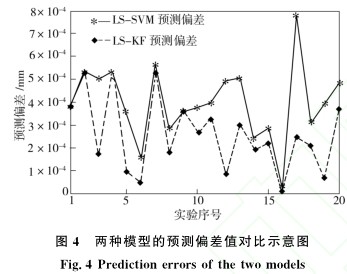
兩種模型的預測偏差值對比如圖4所示。由圖4中可見, Kalman濾波對LS-SVM預測結果的更新從第二次（cì）開始, 即更新結果對訓練模型的調整是從第二次開始的（de）, 而預（yù）測結果（guǒ）的差異會在第三次的預（yù）測結果中出（chū）現, 這就導致圖4中前兩個點的（de）數據是重合的, 而隨著更新步數的增（zēng）加, 兩個模型預測誤（wù）差（chà）的差距也逐漸增大。總的來看,LS-KF模型比LS-SVM模型的（de）預測誤差要小（xiǎo）, 其預測（cè）偏差的平（píng）均值分（fèn）別為0.25μm和0.39μm。

綜上所述（shù）, 所建立的刀具磨損預測模型LS-SVM模型和LS-KF模型均具（jù）有較好預測精度,Kalman濾波確實可以通過更新訓練模型來縮小預測磨損量與實際磨損量之間偏差, 從而進一步提高模型預測精度; LS-KF模型預測結果可以考慮到加工條件及環境的改變對（duì）刀具磨損的影響,其預測精度比LS-SVM模型的預測（cè）精度更高。

4 結語

本文首先建立了基於（yú）LS-SVM的刀（dāo）具磨（mó）損預測模型, 在此基礎上（shàng）建立LS-KF模型, 利用Kalman濾波技（jì）術結（jié）合（hé）刀具實（shí）際磨損（sǔn）量更（gèng）新LS-SVM模型的預測結果, 並將該結果作為實際磨（mó）損量預測下一步的刀具磨損量（liàng）。結果表明, 兩個模型的預測精度均在10%以下, 滿足誤差（chà）的允（yǔn）許範圍。兩個模型中, 結合Kalman濾波技術的LS-KF模（mó）型（xíng）有更高的預測精度, 且可以考慮到加工條件及環境改變對刀具磨損的影響, 所以（yǐ）在加工條件及環境不是完全可控的條件下, 基於LS-KF的刀具磨損預測模型有（yǒu）著更廣泛的應用空間。

投（tóu）稿箱：
如果您有機（jī）床行（háng）業、企業相關新聞稿件發表，或進行（háng）資訊合作，歡迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相（xiàng）關（guān）信息

名企推薦

業界視（shì）點

| 更多

行業數據

| 更多

博（bó）文選萃

| 更（gèng）多