數(shù)控機床熱(rè)誤差(chà)補償模型穩健性比較分析
2017-12-27 來源: 合肥工業大(dà)學儀器科學與光電工程學院 作者: 苗恩銘 龔亞運 徐祗尚 周(zhōu)小帥
摘(zhāi)要:數學模型的精度特性和穩健性特性對數控機床熱(rè)誤差補償技術在實際中的實施(shī)性影響不(bú)容忽視(shì)。對(duì)數控加工中心(xīn)關(guān)鍵點的溫度和(hé)主軸z 向的熱變形量采用多種算法(fǎ)建(jiàn)立了預測模型,對不同算法擬合精度進行分析。同時進行全年熱誤差跟蹤試(shì)驗,獲得了機床在(zài)不同環境(jìng)溫度和不同主軸轉速的(de)試驗(yàn)條件下的敏感(gǎn)點溫度和熱誤差值(zhí)。以此為基礎,對各種預測模型的預測精度進行比較驗證不同模型(xíng)的穩健性。結果表明,多元線性回歸算法的最小一乘、最小二乘估計模型以及分布滯後模型(xíng)在改(gǎi)變試(shì)驗條件時(shí)預測精度下降,而基於支持(chí)向(xiàng)量(liàng)回歸機原理的熱誤差補償模型仍能保(bǎo)持較好的預測精度(dù),穩健性強。這(zhè)為數(shù)控機床熱誤差補償模型的選(xuǎn)擇提供了具有實用價值的參考,具有很好工程應用(yòng)性。
關鍵詞:數控機床;熱誤(wù)差;穩健性;多元線性回歸模型;分(fèn)布(bù)滯後模型;支持向量回歸機
0 前言
在數(shù)控機(jī)床的各種誤差源中,熱誤差已經成為影響零件(jiàn)加工精度主要誤差來源[1]。減少熱誤差是提高數控機床(chuáng)加工(gōng)精度的關(guān)鍵。在熱誤差(chà)補償中,建模技術則是重點。由於機床熱誤差在很大程度上取決(jué)於(yú)加工條件、加工周期、切削液的使用以及周圍環境等等多種因素,而且熱誤差呈現非線性及交互作(zuò)用,所以(yǐ)僅用理論分析來精確建立熱誤差數學模型是相當困難的[2]。最為常用(yòng)的熱(rè)誤差建模方(fāng)法為試驗建模法,即根據統計理論對熱誤(wù)差數據(jù)和機(jī)床溫度值作相關分析。楊建國等[3-5]提出了數控機床(chuáng)熱(rè)誤差分組優化(huà)建模,根據溫度變量(liàng)之間的相關性對溫度變量進行分組(zǔ),再與熱誤差(chà)進行排(pái)列組合逐一比較選出溫度敏感點用於回歸建模。韓國的KIM等[6]運用有限元法建立了機床(chuáng)滾珠絲杠係統的溫度
場(chǎng)。
密執安大學的YANG 等[7]運用小腦模型連接控製器神經網絡建立了(le)機床熱誤差模型。ZENG 等[8]用粗糙集人工神經網絡(luò)對數控機床熱誤差分析與建模,並(bìng)對建模精(jīng)度進行(háng)了論證(zhèng)。CHEN 等[9]運用聚類分析(xī)理論和逐步回歸選擇三坐標測量機熱誤差溫度敏感點,用PT100 測量(liàng)溫度、激光幹涉儀測量三坐標測量機熱(rè)誤差(chà),建立了多元(yuán)線性模型(xíng)。由於這些建模方式是離線和預先建模(mó),而且建模數據采集於某段時間,故用這些方法建立起來的(de)熱誤差數學模型的穩健性顯然不夠,一般隨著季節的變化難以長期正確地預報熱誤差。近年來,支持向(xiàng)量機是(shì)發展起來的一種專門研究小(xiǎo)樣本情況下的機器學(xué)習規律理論,被認為是針對小樣本統(tǒng)計和預測學(xué)習的最佳理論[10]。支持向量機建立在Vapnik-Chervonenkis 維理論基礎上,采用結構風險最小化原則,不僅結構簡單,且(qiě)有效解決了模型選擇與欠學習、過學習、小樣本、非線性、局部最優和維數災難等問題,泛化能力大大提高[11-12]。本文對(duì)Leader way V-450 型數控加工中心進行熱誤(wù)差測量試驗,采用模糊聚類與灰色關聯度理論綜合應用進行(háng)了溫度敏感點選擇,同時利用多元線性回歸(guī)模型,分布滯後模型,支(zhī)持向量回歸機模型分別建(jiàn)立熱(rè)誤差(chà)補償模型,並對多(duō)元回歸模型分別(bié)采用最(zuì)小二乘和最小一乘估計,通過比對(duì)各(gè)種模型的穩健性,從而(ér)為(wéi)數控機床熱誤差補償(cháng)建(jiàn)模(mó)方法的選擇提供(gòng)了參考,具有實際(jì)的(de)工(gōng)程應用價值。
1 、熱誤差建模模型
1.1 多元線性(xìng)回歸模型
多元線性回歸(Multiple linear regression, MLR)是一種用統(tǒng)計方法尋求(qiú)多輸入(rù)和單輸出關係的(de)模型。熱誤差的多(duō)元線性(xìng)回歸(guī)模型以多個(gè)關鍵溫度敏感點測量(liàng)的溫度增量值為自變量,以熱變形量為因變量,其通用表達式為

同(tóng)時(shí),采用最小一乘和最小二乘兩種準則對線性回歸模(mó)型進行估計計算。最小二乘法在方法(fǎ)上較為成熟,在理論上也較為完善,是一種常用的最優擬合方法(fǎ),目前(qián)廣泛(fàn)應用於科學技術領域的許多實際問題(tí)中,在數控機床建模技(jì)術中也(yě)有很多的應用。而(ér)最小一乘法受異常值的影響較小,其穩健性比最小(xiǎo)二乘法的要好(hǎo),但最小一乘回(huí)歸(guī)屬於不可微問題,計(jì)算(suàn)具有較大的難度。文中針(zhēn)對最小一(yī)乘的算法采用(yòng)文獻[13]的算(suàn)法理論和Matlab 程序。最小二乘準(zhǔn)則(zé)——殘差平方和最小,即
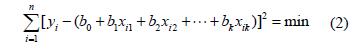

式中 IID ——標(biāo)準正態分布的相互(hù)獨立變量;
n ——最大滯(zhì)後期;
a0 ——常數項;
u ——外生變量個數;
yt ——因變量(liàng);
βj,i ——係數;
xj,ti
——第j 個自變(biàn)量的ti 期值。
對於滯後階數n 的確定,由於試驗測量數據量比較大,所以可(kě)以采用簡單的權宜估計法。即取n=1,2, ,i,對不同(tóng)的i 條件下經最(zuì)小二乘擬合,當滯後變量的回歸係數開始變得統計不顯著,或其中有一個變量的係數改變符號時,i1 就是最終的滯後(hòu)階數。
1.3 支持向量回歸機模型
統計學習理論是由VAPNIK[11]建立的一種(zhǒng)專門研究有(yǒu)限樣本情況下機器學習規(guī)律(lǜ)的理(lǐ)論,支持向量機是在這一理論基(jī)礎上發展起來的一種新的分類和回歸工具。支持向量機通過結構風險最小化原理(lǐ)來提高泛化能力,並(bìng)能較好地(dì)解(jiě)決小樣(yàng)本、非線性(xìng)、高維數、局部極小點等實際問(wèn)題,其已在模(mó)式識別、信號處理、函數逼近等領域應用。


引入拉格朗日函數,可得凸二次規劃問題



2 、試驗(yàn)設計
2.1 試(shì)驗方案
本文對Leader way V-450 數控加工中心主(zhǔ)軸z向進行熱誤(wù)差測量試驗(yàn),各傳感器的安放位(wèi)置及作用如表1 所示,溫度傳感器和電(diàn)感測(cè)微儀具體分布位(wèi)置如圖(tú)1 所示。

圖1 熱誤差(chà)測量試驗
表1 傳感器安放位置及作用
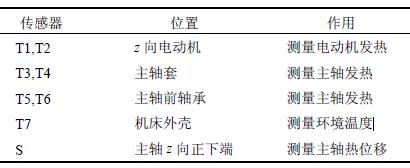
試驗對數控加(jiā)工中心在(zài)不同季節(不同環境溫度(dù))、不同主軸轉速下進行了9 次熱誤(wù)差測量試(shì)驗,測量(liàng)的次數、轉速及環境溫(wēn)度如表2 所示。
表2 試驗(yàn)批次的主軸轉速和環境溫度
表2 中,Knm 含義是,第n 次測量(liàng)的主(zhǔ)軸轉(zhuǎn)速在m 的試驗(yàn)數據。如K12000 表示第一次測量的主軸轉速在2 000 r/min 的試驗數據,K22000 表示不同環境溫度下第二次測量的主軸轉速在2 000 r/min 的試驗數據,K32000 表示不同環境溫(wēn)度(dù)下第三次測量的主軸(zhóu)轉速在2 000 r/min 的試(shì)驗數據。
2.2 溫度敏(mǐn)感點(diǎn)的篩選
為便於(yú)實際(jì)工程應用,針對溫度傳感器數目進行(háng)優化挑選,合理有效地篩選溫度傳感器有助於提高機床熱誤差建模精度。本文采用模糊聚(jù)類與回(huí)歸關聯度相結合的方法選擇熱誤差關鍵(jiàn)敏感點,具體方法(fǎ)參考文獻[15],最終選擇T6 和T7 作為溫度(dù)敏感點。
3 、建模(mó)模型的穩健性分析
穩健(jiàn)性是指在模型與實際對象存在一定差距時,模型依然具有較滿意的模擬預測性能。本文利用多元線性回歸的最(zuì)小二乘、最小一乘估計模型,分布(bù)滯後模型以及支(zhī)持向(xiàng)量回歸機模(mó)型對(duì)K16000 數據分別建立預測模型(xíng),先進行各模型對本批數據的擬合精(jīng)度進行分析,隨後將該模型用於(yú)其他批次采樣數據的預(yù)測,以判斷模型的穩健(jiàn)性。同時,根據建模數據的來源批次特征,對各算法給予了穩健性分析。
3.1 不同(tóng)算(suàn)法的模型(xíng)擬合精度分析



表3 各模型的擬合標準差 μm

由表3 可知,擬合精度SVR 最優,DL 其次,擬合精度最(zuì)差的是(shì)MLR 最小一乘算法。
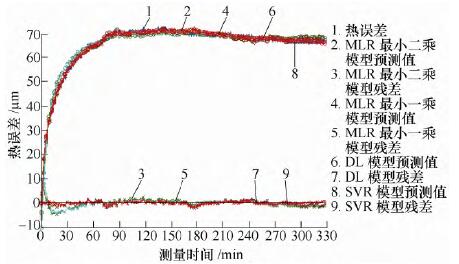
圖2 對K16000 擬(nǐ)合效果
為比對各算法穩健性,利用各個模型建立的預測模型對其餘批(pī)次(cì)數據按照同(tóng)轉速不(bú)同溫度(dù)(環境溫度變化範圍較大)、同(tóng)溫度(環境溫度變化較小)不同轉速、不同溫度(dù)(環境(jìng)溫度變化範圍較大)不同轉速三種類型進行數(shù)據預測,根據(jù)預測效果對(duì)各個補償模型進行穩健性分析。
3.2 同轉速不同環境溫度分析
以K16000 數據建立的預測模型對K26000 數(shù)據進(jìn)行預測精度分析,分析效(xiào)果如(rú)圖3 所示;再對K36000數據進行預測精度分(fèn)析(xī),分析效(xiào)果如圖4 所示。各個預測模型的預測標準差如表4 所示。
表4 各模型的預測標準差 μm
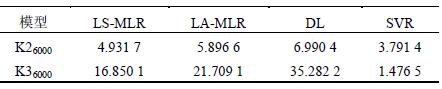
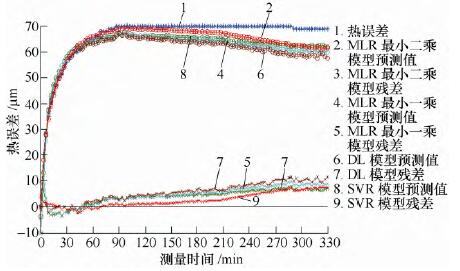
圖3 對K26000 預測效果
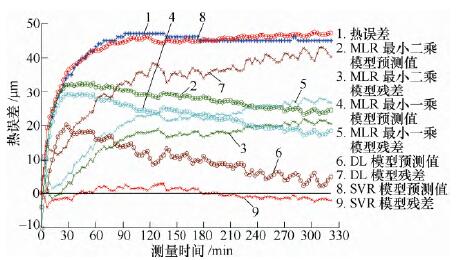
圖4 對K36000 預測效果
通過分析比較可得,轉速不變(biàn),環境溫度增加較小時,各個預測模型的預測效果(guǒ)仍然保持較好,但是隨著環境溫度增加較大時,多(duō)元線性回歸(guī)的最小二(èr)乘、最小一乘模(mó)型以及(jí)分布滯後模型的預測效果變差,其中多元線性回歸的最小二乘算法相對較好,隨後是最小(xiǎo)一乘模型,預測效果最差的是分布(bù)滯後模型。除此之外,支(zhī)持向量回歸機模型仍能保(bǎo)
持很好的預測精度。
3.3 同(tóng)溫度(dù)不同轉速分析
針對溫度(dù)變化範圍較小的(de)不同轉速測量數據(jù),以K16000 數據建立的預測模型對K14000 和K12000 數據進行預測(cè)精度分析,根據分析數據結果來判斷不同算法建立的模型的穩健性(xìng)。先對K14000 數據進行分析,分析效(xiào)果如圖5 所示;然後分析K12000 數據,分析效果如圖6 所示。各個預測模型的預(yù)測標準差如表5 所示。
表5 各模型的預測標準差 μm
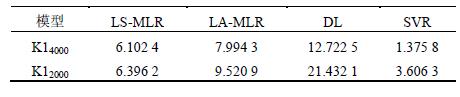
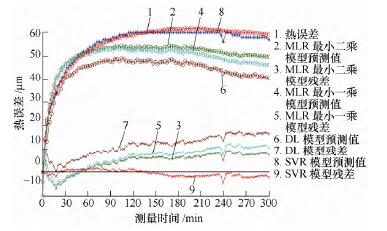
圖5 對K14000 預測效果
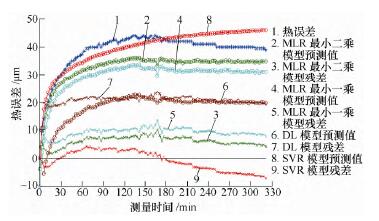
圖6 對K12000 預測效果
通過分析比較(jiào)可得,環境溫度基本不變,轉速(sù)逐漸降低時,最(zuì)小二乘和最小一乘模型仍具有一定的預測精度,分布滯後(hòu)模型預(yù)測效果越來越差,而支持向量回歸機(jī)模型始終保持很(hěn)好的預測精度。各算法穩定性優劣依(yī)次為支持向量回歸機模型、最(zuì)小二乘、最小一乘和分布滯後模(mó)型。
3.4 不同溫度不同轉速(sù)分析(xī)
針對環境溫度變化時的不同轉速(sù)測量數據,以K16000 數據建立的預測模型對(duì)K24000、K22000、K34000和K32000 數據進行預測精(jīng)度分析,根據分析數據結(jié)果來判斷不同算法建立的模型的穩(wěn)健性。各個預測模型的預測(cè)標準(zhǔn)差如表6 所示。
表6 各模型的預(yù)測標(biāo)準差 μm
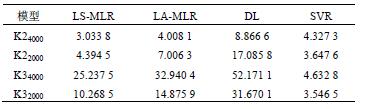
通過分析(xī)比較可得,環境溫度變化幅度較小,轉速逐漸降低時,最小二(èr)乘和支(zhī)持向量回歸機模(mó)型具有很好的預(yù)測(cè)精度,最小(xiǎo)一乘模型的預測精度逐漸降(jiàng)低(dī),分布滯後模型(xíng)預測效果逐漸變差;環境溫(wēn)度變化幅度較大時(shí)(超過10 ℃),轉速逐漸降(jiàng)低時,隻有支持向量回歸機模型(xíng)仍保持較好(hǎo)的預(yù)測精度,其(qí)他的預測(cè)模型的(de)預測效果很差。各算法穩定(dìng)性優劣依次為支持向(xiàng)量回歸機模型、最小二乘、最小一乘和分布滯後模型。
4 、結論
(1) 通過長期(qī)測量數控機床熱誤差和關鍵敏感點溫度來獲得多(duō)批次的試驗數據,通過(guò)多種模型算法(fǎ)進行了(le)預測建模(mó),從機床主(zhǔ)軸(zhóu)同轉速不(bú)同(tóng)環境溫度、同環境溫度不(bú)同轉速(sù)、不同轉速(sù)不同環境溫度等三種情況對預測模型(xíng)的精度與穩定性進行了分析。
(2) 從試驗(yàn)效果可知,分布滯後模型具有很(hěn)好的擬合精度,但(dàn)以一組采樣數據建立(lì)的分布(bù)滯後模型其穩健性較差。僅以一組采樣數據進行建模,最小一乘模型的穩健性並不優於最小二乘模(mó)型,反(fǎn)而略差(chà)。最(zuì)小一乘法穩健性高於最小(xiǎo)二乘法的(de)說法,是基於對異(yì)常數據處理方麵的優勢,而數控機床熱變(biàn)形(xíng)測量數據中出(chū)現(xiàn)異常數據的概(gài)率很小(xiǎo),使得該
法的優勢並(bìng)未得到體現,而且數控機床熱誤差數據樣本量較大,最小一乘算法複雜,相對於最小二乘(chéng)法,最小(xiǎo)一乘法在數控機床熱誤(wù)差預測建模(mó)中的實際應用效果反而不如(rú)最小二乘法(fǎ)。
(3) 支(zhī)持向量回歸機模型擬合精度高,預測(cè)效果保持(chí)性好,穩健(jiàn)性強,該算法作為數控機床熱誤差補償的建模算法具有工程應用基礎。
投稿箱:
如果您(nín)有機床行業、企業相關新聞稿(gǎo)件發(fā)表,或(huò)進行資訊(xùn)合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您(nín)有機床行業、企業相關新聞稿(gǎo)件發(fā)表,或(huò)進行資訊(xùn)合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息
業(yè)界視點
| 更多
行業數據
| 更多
- 2024年11月 金屬切削機床產(chǎn)量數據
- 2024年11月(yuè) 分地區金屬切削機(jī)床產量數(shù)據(jù)
- 2024年(nián)11月(yuè) 軸承出(chū)口情(qíng)況
- 2024年11月 基本(běn)型乘用車(轎車)產量數據
- 2024年11月 新能源汽(qì)車產量數據(jù)
- 2024年11月(yuè) 新能源汽車(chē)銷量情況(kuàng)
- 2024年10月 新能源汽車產量數據
- 2024年10月 軸承出口情(qíng)況
- 2024年10月(yuè) 分地區金屬切削機床產量數據
- 2024年10月 金屬切削機床產量數據
- 2024年9月(yuè) 新能源汽車銷量(liàng)情況
- 2024年8月 新能源汽車(chē)產量數據
- 2028年8月 基本型乘用車(轎車)產量數據(jù)
博文選萃
| 更多





