基於剛體動力學的五軸數控機床模擬係統研究
2016-8-1 來源:天津職業技術(shù)師範大學 作者:嶽剛
把操作者手工編寫(xiě)或通過軟件自動編寫的工件加工(gōng)程序,翻譯成運動控製卡可以識別的刀具路徑軌跡,是數(shù)控係統的主要工作之一(yī)。這(zhè)個識別(bié)過程實際上是將工件加(jiā)工程序中工件坐標係中的刀具路徑(jìng)軌跡經過一定的計算[20],轉變成為機床(chuáng)坐(zuò)標係中的刀具路徑軌跡。所以必須正確的對刀具路徑軌跡(jì)進行(háng)運(yùn)動求解計算才能實現該過程。五軸數控機床通過在三個線性軸運動的基礎之上增(zēng)加了兩個回轉軸的運(yùn)動[21],其運動的複雜性也相應的增加,對於編程人員和機床操作人員來講,增加了一(yī)定(dìng)的難度。對五軸數控機床進行正確(què)的運(yùn)動求解,有利於深入掌握它的(de)運動規律,最大程度地發揮其在加工(gōng)中高效、高精等優勢。
從(cóng)數學(xué)的角度講,物體運動求(qiú)解的本質就(jiù)是三維圖形的線性變換,其中包括基礎線性變換,諸如平移變換、旋轉變換等。當前國內外相關行業的研發人員已開始對(duì)適合五軸數控機床進行分析的通用算法的探究,不過目前針對五(wǔ)軸數控機床的運動分析大多是在假定(dìng)機(jī)床所有移動軸一一正交等限製條件下進行的[22],並且也沒有考慮機床本身的製造精度。所以,綜合考慮多因子的五軸(zhóu)數控機床運動分析理論的探究是今(jīn)後五軸數控(kòng)機(jī)床運動學探究最主要的領域之一。
本章在描述了運動分(fèn)析(xī)時所必須借助的基礎線性代數原理,分別例舉了采用三種非常普遍(biàn)的構(gòu)成形式的五(wǔ)軸數控機床在(zài)一定的限製條件下的運動分析算法。因為機床的(de)製造精度與安裝精(jīng)度(dù)有一定限製(zhì),故對於五軸數控機床(chuáng)進行運動分析還需(xū)要結合機床自身具有的許多誤差,來(lái)修正這些誤差對工件切削精度的影響。
3.1 運動分析
在三維空間中,任何物體的運動方式都可以概括為幾何體(tǐ)的平移、旋轉等許多(duō)基(jī)礎的(de)線(xiàn)性(xìng)變換[23]。從線性代數的角度講,這些變換全部可以看做幾何體的幾何變換,因此(cǐ)又把幾何體的線性變換稱為幾(jǐ)何變換,上述的變換能夠通過線性代數中的矩(jǔ)陣乘(chéng)法來完成。
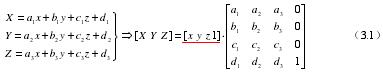
3.1.1 平(píng)移變換
幾何體在三維空間從一個坐標點沿著任意直線運動到另(lìng)一個坐標點的過程叫(jiào)做平移變換[23],在整個(gè)變換中不會使幾何體的外形和尺寸發生變化。對應的齊次方程為:

假定空間幾何體的起(qǐ)始位置為(x,y,z),在(zài)整個運動過程中,幾何體沿著 X、Y、Z 三個方向(xiàng)各(gè)運動了 u、v、w 個單位長度,運動結束後,新的(de)位置為(X、Y、Z),那麽該(gāi)幾何體的位置變換對應的方程為:

3.1.2 旋轉(zhuǎn)變換
所(suǒ)謂旋轉變換,就是讓某個物體繞著 X、Y、Z 三個軸中的一個軸旋轉(zhuǎn)一個角(jiǎo)度。此時,可以利用(yòng)右手螺旋法則來判斷轉角的正負[24][36]。(1)圍繞 X 軸轉動,X 方向坐(zuò)標不(bú)發生變化(huà),隻有 Y、Z 兩個方向坐標發生變化。對應的方程為:
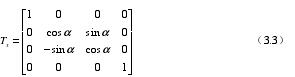
(2)圍繞 Y 軸轉動,Y 方向坐標不發生變化,隻有 Z、X 兩個(gè)方向坐標發生變(biàn)化。對應的(de)方程為:
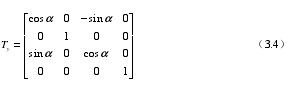
(3)圍繞 Z 軸轉動(dòng),Z 方(fāng)向坐標不發生變化,隻有 X、Y 兩個(gè)方(fāng)向坐標發生變化。對應的方程為:
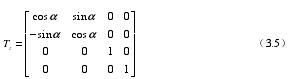
3.1.2.1 圍繞過(0,0)點(diǎn)的任意(yì)直線的旋(xuán)轉(zhuǎn)變換
直線 OD 是給定三維坐標係中過(0,0)點的任意直線,點 F 是坐(zuò)標係中(zhōng)任一不在直線OD 上的點(diǎn),若點 F 圍繞直線 OD 轉動(dòng)後與 G 點(diǎn)重合,那麽相應旋轉變(biàn)換的計算方(fāng)法為[25]:
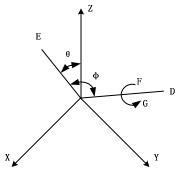
圖3-1 繞過坐(zuò)標原點直線的旋(xuán)轉
(1)令直線 OD圍繞 X 軸(zhóu)轉動轉角後(hòu)與麵 XOZ 重合,新的直線成(chéng)為 OE。這個變換能夠用式 3-3 來完成。
(2)令直線 OE 圍繞 Y 軸轉動轉角 θ 後與 z軸重(chóng)合,這個(gè)變(biàn)換能夠用式 3-4 來完成。
(3)使用式 3-5 令點 P 圍繞 Z 軸轉動轉角 α。
(4)運算和(2)中互逆,也就是(shì)令直線 OE 圍繞 Y 軸旋轉轉角(jiǎo)-θ,即使用式 3-4 的互逆矩陣來完成。
(5)運算(suàn)和(1)中互逆,即使用式 3-3 的互逆矩陣來完(wán)成。最後能夠獲得圍繞過(0,0)點的任意直線 OD 的旋轉矩陣1 1R x y z y xT T T T T T= 。
3.1.2.2 圍繞過其他已知點的任一直線的旋轉變換
L 是三維空間中過點的任一直線(xiàn),它的方向向量(liàng)是,那麽空間幾(jǐ)何體圍繞直線 L 轉動轉角的相應轉換能夠分為如下三步:

圖(tú) 3-2 繞過任意(yì)點 P 直線的旋轉變換
(1)通過空間幾(jǐ)何體與直線(xiàn) L 共同進行平移(yí)令點 P 移動到(0,0)點位置,轉換矩陣pT為:
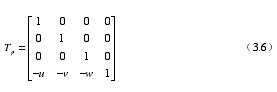
(2)在前一個步驟完成之後,令空間幾何體圍繞 L 轉動轉角α ,對應轉換矩陣是RT 。
(3)令空間幾何體與 L 共同(tóng)進行平移變換回到最初坐標,對應轉換矩陣是1PT:

最後,能夠獲(huò)得總的(de)轉換矩陣:
3.2 常見五軸數(shù)控機床的構(gòu)造模式(shì)
從三維幾何的角度講,每一個物體都擁有六個獨立的自(zì)由度[27]。舉個例(lì)子,對於一個工件來說,工件的位置是固定的,所(suǒ)以,對於工件來說,主(zhǔ)軸就具備了六(liù)個獨立的自由度。在加工過程中(zhōng),主軸上的刀(dāo)具對(duì)工件進行切削,這時刀具軸線也就是主軸軸線和工(gōng)件之間的距離受(shòu)到刀具半徑的限製,因(yīn)而實際(jì)上隻(zhī)有五個自(zì)由度可用,理論上講實現(xiàn)五軸(zhóu)聯動就可以完成所有空間(jiān)複雜曲麵的(de)加工[28]。
五軸數控機(jī)床通常指擁有五個以上可聯動軸的數控機床[29],依據不同的自由度(dù)組合(hé)方式也就是固定或變相固定(dìng)哪一個的自由度,理論上能夠形成成四種不同(tóng)的組合,依次為:X、Y、Z 三個軸方向上的自(zì)由度和繞(rào)任意兩個軸回轉的自由度組合、任(rèn)意兩個直線方向自(zì)由度和(hé)三個回(huí)轉自由(yóu)度組合、一個(gè)直線方向(xiàng)自由度和四個回轉自由度組合(hé)、五個回轉自由度。但在實際使用過程中,需要考慮機床的綜合性能,特別是(shì)加工精(jīng)度、係統壽命等關鍵要素,所以,當前市場上(shàng)常見的五軸數控機床(chuáng)都普遍采用第一種方式的自由度組合[30]。依據不同的回轉自由度(dù),還能夠對五軸聯動(dòng)數控機床進行細分,可以分為三(sān)種,分別是:雙旋轉主軸頭(tóu)式、雙回轉工作台式、一回轉工作台加一旋轉主軸頭式[31]。
(1)雙旋轉主軸頭式
雙旋轉主軸頭式的五軸聯動數控機床示意圖如圖 3-1 所示(shì)。從圖中(zhōng)能夠(gòu)發現,機床的兩個回轉自由度(dù)全部布置(zhì)在主軸上,使得刀具能夠前後左右進行擺動,這樣理論(lùn)上可以使刀具繞中心點轉(zhuǎn)動到任意位(wèi)姿[32],對(duì)於此類機床,其工作台無(wú)需進行轉動,因此工(gōng)作台的大小不受約束,允許設計者設計大型機床。這樣的布置形(xíng)式的特點在於機床整體承載性能大大增(zēng)強[33],同(tóng)時加工空間也基本不受限製,其加工對象為(wéi)大型工件,所以大(dà)型龍門式五軸(zhóu)聯動數控機床普遍的(de)采(cǎi)用這種結構。此類機床兩個旋轉軸(zhóu)全部集中到了刀(dāo)具的上部,回轉軸部(bù)分結構緊湊,加工過程靈活(huó);同時缺點也很明顯,因為主軸頭集成的擺動機構與傳動機構過於(yú)複雜,使(shǐ)得整個機(jī)床的剛度被大大降低。
(2)一回轉工作台加一旋轉主軸頭(tóu)式
這種類型的機床通過在機床的主軸頭上麵加一個回轉自由度,另外一個回轉自由度加在工作台上,主要(yào)通過加載在主軸和工作(zuò)台上(shàng)的兩個方向的回轉自由(yóu)度,這樣布(bù)置的好處就是兩(liǎng)個回(huí)轉軸的軸線方向都是(shì)固(gù)定不變的[33],其示意圖如圖3-2 所示。這種結構的五(wǔ)軸機(jī)床,因為兩個方向的(de)回轉運動並未集中在一(yī)起(qǐ),所以采用這類布(bù)置方式(shì)的五軸數控機床(chuáng)優點是結構(gòu)簡單、整體剛(gāng)性好,缺點是靈(líng)活性不好。由於隻有一個回轉自由度在工作台上,導致整個機床的承載性能差,並(bìng)且隻能承擔的尺寸相對較小的加工任務,通常用來進行中等尺寸工(gōng)件的切削。

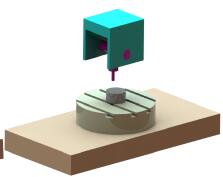
圖3 -1雙旋(xuán)轉主軸頭(tóu)結構五軸機床(chuáng) 圖3 - 2一擺動頭和一回轉台結構五軸機床
(3)雙回轉工作(zuò)台(tái)式
這種類型的五軸聯動數控機(jī)床(圖3-3)是由工作台承(chéng)擔兩個回轉自由度的,因為(wéi)主軸和工作台的運動是相對的(de),所以不論旋轉(zhuǎn)自由度布置在主軸上還是布置在工作台(tái)上,都能達到同樣的(de)加工效果從傳動鏈的先後順序能夠知道,采用這種布置方(fāng)式的機床的兩個旋轉軸有一個是定軸另一個是動軸。定軸就是指遠(yuǎn)離工件的隻具(jù)備一個旋轉自由度的(de)軸[34],這個軸圍繞(rào)的(de)軸線(xiàn)方向在加工過程中是不會(huì)改(gǎi)變的;動軸是指跟著加工工件一同(tóng)擺動的旋轉軸,其所圍繞的旋轉軸線方向跟著一個定軸的運動而旋轉。采用這種布置(zhì)方(fāng)式的機床承載性能最差(chà),加工尺寸範圍最(zuì)小,整個係統剛性處於中等水平,通常用於中小尺寸工件的切削加工[35]。
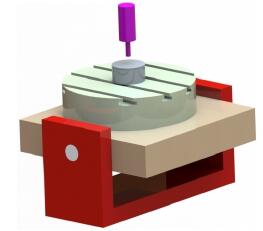
圖3-3雙回轉(zhuǎn)工作台結構五軸機床
綜上所述(shù),無論五軸機床采用哪種布置方式,都同樣可以做到刀具對工件的(de)任意角度切(qiē)削。因為機床擁有兩個旋轉(zhuǎn)自(zì)由度,刀具可以(yǐ)在機床結構的限製下的任意空間角度對工件進行切削。在相應運動控製算法的支持(chí)下,能夠確保在整個(gè)切削過程中,刀具按(àn)照最佳的位姿來加工,而且可以(yǐ)防止機床發生運動幹涉[36]。所以,五軸聯動數(shù)控機床具備三軸、四軸機床所不(bú)具備(bèi)的的優越的性能(néng),能完成分任務更多,同時精度會更高[37]。
重點研發五軸數控機床模擬訓練機(jī)的意義在(zài)於:學習數控係統最好的方式是(shì)在實際機床上進行練習(xí),但是這樣需要大量的五軸數控機床,這對於學校來說是不現實的[38]。五軸數控機床(chuáng)模擬訓練機是國內首創(chuàng)能夠解決數控係統教學(xué)問題、數控編程人員學習問題的一個關鍵產品。
3.3 五軸數控機床的運(yùn)動(dòng)求解(jiě)
3.3.1 雙轉台型五軸數控機床的運動求解
雙回轉台型(xíng)五軸數控機床按照(zhào)旋轉軸的(de)不同,能夠具體分為 AB、BC、AC 三種[39]。因為這(zhè)三種不同選擇方式(shì)的運動變換計算過程沒有太大差別,所以在這裏隻探討了最(zuì)常(cháng)見的(de) AC 型組合(hé)方式的運動變換計算(suàn)過程(chéng)[40]。
傳統三軸數控機床隻具備 X、Y、Z 三個直線方向的(de)自由度[41],所以沒有必要進行其他(tā)的(de)分析、數學建模、運算,隻需要將程序中(zhōng)的有關路徑控製方麵的 G 代碼翻譯成 XY、Z 三個軸方向上的運(yùn)動量,然(rán)後再進行聯合插補運動,最終就(jiù)能夠驅動三個運動軸(zhóu)切削工件。五軸數控機床除了擁有 X、Y、Z 三個軸之(zhī)外還有另外兩個回轉軸[42],使(shǐ)得刀具可以相對於工件(jiàn)做直(zhí)線移動和(hé)回轉運動,所以在刀路運動計算上,需要六個數據來(lái)表達某一瞬時的刀尖點位置及刀具軸線位姿:(X, y , z )表示加工刀尖點的位(wèi)置,( i , j , k )表示加工刀具軸線的位(wèi)姿[43]。
在五(wǔ)軸機床(chuáng)中,刀具在對工件進行切削之前,需要嚴格采用五軸機床上的(de)結構形(xíng)式對其整個運動、切削過程進(jìn)行(háng)運動學分析,找出工件坐標係與機(jī)床(chuáng)坐標係的聯係,推算(suàn)出其(qí)中的轉(zhuǎn)換矩陣,充分利用(yòng)這個轉(zhuǎn)換矩陣[44],能夠精確的轉換(huàn)某一瞬時的刀尖點位置及刀(dāo)具軸線位姿為 X、Y、Z 三個軸的移(yí)動和 A 、C 兩個旋轉軸的轉動,這一點是保證數控程序能夠正確被編譯的基礎。本節(jiē)會針對此推導過程做詳(xiáng)細討論[45]。
如圖 3-4 所示,記工件原點坐(zuò)標係為m m m0X Y Z ,機床原點(diǎn)坐標係為t t tO X Y Z ,以 A、C兩軸中心線交點作為機床坐標原點[46]。工件(jiàn)原點坐標係m m mO X Y Z 和機床原點坐(zuò)標係t t tO X Y Z 共享同一個 Z 軸方向,m t0 O =d 。工作台的回轉能夠帶動毛坯進行位姿變換,其中 A、C 兩軸的轉動範圍分別為 0°≤A≤90°、0°≤C≤3600°。
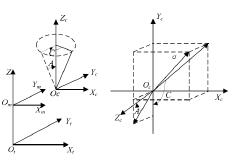
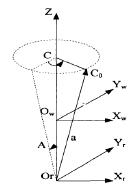
圖 3-4 坐標係 圖3 - 5雙轉台型五軸數控機(jī)床坐標係
為了方便以後的計算,需要定義(yì)一下計算過程(chéng)中用到的坐標係:令(lìng)零(líng)件坐標係(xì)為w w w wO X Y Z ,零(líng)件能夠在兩個回轉軸的運動中完成圍繞 X 軸轉動轉角(jiǎo) A( 0° ≤A ≤90° ),圍繞 Z 軸轉動轉角 C;機床的移動坐標係為r r r rO X Y Z 。同時(shí),w rO O =d ,如圖 3-5 所示;當前刀具的刀心點0C ,其在(zài)零件坐標係內的坐標假定為(wéi)(0 0 0, ,C C CX Y Z );當前刀具的軸線假定為α (單(dān)位矢(shǐ)量),其在零件坐標係(xì)內(nèi)假定為( , ,)x y zα α α[48]。
在以上設定的基礎上,AC 型組合方式(shì)的運動變換計算過程具體如下:
(1)首先將刀具軸線α 移(yí)動到經過零件坐標係的原點,之後令它圍繞 Z 軸轉動到平麵(-Y)(+Z)內,最後(hòu)把刀具軸線α 圍繞 X 軸轉動到和 Z 軸重合[49]。以(yǐ)上工作的出發點是要確保當 0zα ≥ 時,令刀具軸線 α 圍繞 X 軸轉動轉(zhuǎn)角處於 (90° 0°) 之(zhī)間,也就是刀具相對於零件圍繞 X 軸轉動轉角處於(0° 90°) 之間。
(2)將刀具軸線(xiàn)α 的轉動轉化成刀具的旋轉或移動:首先讓刀具圍繞 X 軸轉動(dòng)某個角度 A,再將刀具圍繞五軸機床(chuáng)德爾 Z 軸轉動一定角度 C。所(suǒ)以(yǐ)能夠獲得 A 角的運算過程如下:
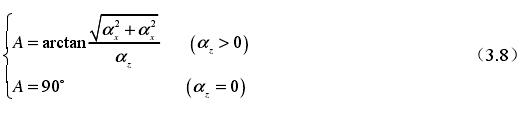
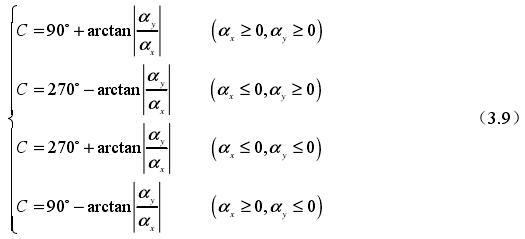

(3)零件坐標改變後,刀具的中心點0C 坐標值也(yě)會發生變化,則機床坐標係內的坐標值 X、Y、Z 的運算方法為:
1)對零(líng)件工(gōng)件坐標係w w w wO X Y Z 進行移動,使得兩個(gè)坐標係的rO 和wO 重合(hé),相應的轉換矩陣是:

2)使零件圍繞五軸數控機床的 Z 軸轉動角度 C,對應的轉換矩陣是:
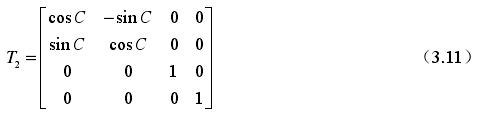
3)使零件圍(wéi)繞五軸數控機床的(de) X 軸轉(zhuǎn)動一個角度(dù) A,相應(yīng)轉換矩陣是:

則有:
將上式展開可得:
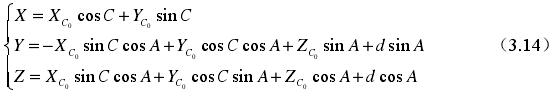
3.3.2 雙擺頭型五軸數控機床的運動求解
雙(shuāng)擺(bǎi)頭型五軸數控機床根據不同的旋轉軸,可以細分為三種方式[50]。因為這三種不同選擇方式的運動變換計算過程沒有太大(dà)差(chà)別,所以在這裏隻探討了最(zuì)常見的 X,Y,Z,A,C 組合方式的運動變換計算過程[51]。
首先,初定零件坐標係為w w w wO X Y Z ,假定讓刀具繞 Z 軸旋轉一定角度 C,再讓刀具圍繞 X 軸旋轉一定角度 A(0 ≤A ≤90);假定刀具的轉動中心0hC 至刀心點0C 的空間上的(de)直線距離是 L,如圖(tú) 3-6 所示。此(cǐ)時(shí),刀心點0C 處在零(líng)件坐標係內的位置為0 0 0(, , )C C CX Y Z ,同(tóng)時,刀具軸線α (單位矢量)在零件坐標係(xì)內可用( , , )x y zα α α 來表(biǎo)示。那麽(me),機床坐標係內移動變換(huàn)可以表(biǎo)示為:
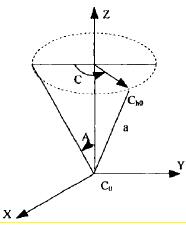
圖 3-6 雙擺頭型五軸數控(kòng)機床坐標係
A、C 角的計算過程和前一節裏(lǐ)的(de)計算過程並無(wú)差別,在這裏(lǐ)就省略(luè)了。
刀(dāo)具中心0hC 在刀具旋轉和移動後位於零件坐標(biāo)係w w w wO X Y Z 內的坐標,就是機床坐標係下 X,Y,Z 坐標值,其(qí)計算過程為:
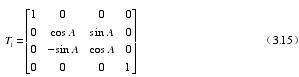
(1)如圖所示,刀具中心以刀心點0hC 為固定點轉動轉角0C ,圍繞 X 軸轉動轉角 A,它的(de)轉換矩陣是:
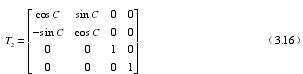
(2)刀具中心以刀(dāo)心點0hC 為固定點轉動轉角(jiǎo)0C ,圍(wéi)繞 Y 軸旋轉轉角 C,它的轉換矩陣(zhèn)是:
(3)經過以上轉換之後,刀具中心位於零件坐(zuò)標內的位置能夠通過下麵的方程來計算:
將上式展開得:
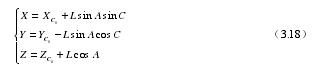
3.3.3 非正(zhèng)交五軸數控機床的運動求解
這(zhè)種運動方式(shì)的求(qiú)解與以上(shàng)兩(liǎng)類運動變換相似,計算過程並沒(méi)有很大的差別,非正交結構(gòu)五軸數控機床的運(yùn)動可以具體劃分為幾下(xià)三步進行變換計算[52]:
(1)計算從零件坐標係轉換至機床坐標係的位置轉換矩陣。
(2)計算相對於起始點的兩個轉動軸(zhóu)的轉角。
(3)把零件坐標(biāo)係內具體的刀位點位置變(biàn)換成實際機床坐標係中的坐標值[53]。因為本文(wén)具體討論(lùn)的是(shì)雙轉台正交構(gòu)造(zào)的(de)五軸數控機床,並且非正交構造五軸數控機床的移動變換計算過程相對繁瑣(suǒ),所以本文不討論。
3.4 本章小結
伴隨著電子計算機科技、數字控製算法(fǎ)的飛速進步,切削加工工件複雜程度的增加等,五軸數(shù)控(kòng)機(jī)床在構造構成(chéng)以及(jí)數字控製算法(fǎ)上均表現出多樣化的發展態勢[54]。本章首先闡述了平移、旋轉等對機床進(jìn)行運動求解時必需的一些基本(běn)數學理論。接著從結(jié)構形(xíng)加工性(xìng)能等角度,對(duì)雙轉台型、雙擺頭型、擺頭轉台型以及非正交型五軸數控機床進行了詳細的介紹,並詳細(xì)了研究了上述(shù)幾種常見類(lèi)型機床的運動求解算法[55]。本(běn)章在描述了運動分析時(shí)所必須借助(zhù)的基礎線性代數原理,分別例舉了采用三種非常普遍的構(gòu)成形式的五(wǔ)軸數控機床在一定的限製條件(jiàn)下(xià)的運動(dòng)分析算法[56]。同時(shí),為下一(yī)章的進一步研究做(zuò)了鋪墊,為模擬機訓練係統操作(zuò)模塊研究奠定了基礎。
投稿箱:
如果您有機床(chuáng)行業、企業相關新聞稿件發(fā)表,或進行資(zī)訊(xùn)合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床(chuáng)行業、企業相關新聞稿件發(fā)表,或進行資(zī)訊(xùn)合作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com
更多本專(zhuān)題(tí)新聞(wén)
專題點擊前十
| 更多










