摘要：電火花銑削可利用簡單電（diàn）極（jí）以（yǐ）逐層掃掠的方式有效加工複雜三維型腔。采用定（dìng）長補償方法配（pèi）合電極旋轉進行電火花銑削加工，電極端麵會形成圓錐（zhuī）形，經過兩刀銑削加工後第一層的加工麵會呈現波浪形。針對波（bō）浪麵對加工精度的影響進行了仿真分析，結果表明波浪（làng）麵對最終的型（xíng）腔（qiāng）底（dǐ）麵形狀幾乎不（bú）產生影響。為獲取（qǔ）最佳一層（céng）表麵以減小對後續加工影響，確定了第一層第二步加工的最佳深度的定義；並通過三角形假設和正弦曲（qǔ）線假設從幾何上找到了最佳深度的取值（zhí）範圍。通過實（shí）驗驗證了理論模型並進一步（bù）細化最佳深度取值區間，為後續精確加工奠定了基礎（chǔ）。
   
      關鍵詞：電火花銑（xǐ）削；定長補償；三維型腔；底麵輪廓；仿真
   
      1 、研究背景介紹
   
     隨著社會（huì）技（jì）術的發展，各行業（yè）對產（chǎn）品微小化的需求（qiú）不斷提升， 微細加工技（jì）術也得到了（le）廣泛關注。微細電火花銑削加工是利（lì）用簡單電極在數控係統控製下，按一定軌跡作成形運動（dòng）以獲得所需工件形狀的加工方法。其依靠電蝕作用蝕除工件材料，因此可用來加工傳統加（jiā）工中難以製作的（de）超硬材料。在複雜三維實體製造過程中，其使用簡單形狀的管狀電極或棒狀電極，采用逐層掃掠的方式由二維麵疊加而成，省去了複雜的成形電（diàn）極的製備過程，節約了時間和成本，提高了加（jiā）工效率，增加了製造柔性[1]，是三維行（háng）腔加工的一種有效方法。
 
 
     在銑削加工中（zhōng），由（yóu）於使用的管狀或棒（bàng）狀電極的截麵積遠遠小於要加工型腔的（de）截麵積，所以在電極在長度方向上的損耗量十分巨大，直接影響到加工精度，嚴重地製約了電火花銑削的實際（jì）應用[2]。國內外研究學者在電火花銑削補償方麵做了（le）大量研究。Yu 率先提出了等損耗的概念，並利用（yòng）這種方法加工出了複（fù）雜三維（wéi）型腔。Bleys 提出了（le）一種聯合補償方法，即將預測（cè）補償和實時補償相結合，以避（bì）免加工過深所帶來的誤差[3-4]。Bissacco 和（hé）Mahardika 等提出了基於放（fàng）電參數檢測的補償（cháng）方法，實現了對電極損（sǔn）耗的實時補（bǔ）償[5-6]。此外，Yan 提出了基於（yú）CCD 的圖像識別法，比較了在（zài）不同（tóng）的銑削深度和（hé）電極旋轉與否的情況下電極的損耗情況[7]。大連理工（gōng）大學又在等損耗的基礎上提出（chū）了均勻損耗分段補償方法（fǎ），基於網格劃分的（de）電極損耗補償方法，以及變分（fèn）層厚度（dù）等方法[8-10]。遲關心提出（chū）了采用（yòng）管狀電極進行電火花銑削加工的方（fāng）法，提高了加工表麵修正精度和銑削效率[11]。周勇[12]提出了一種工具電極軸向補償的方法，並（bìng）在實（shí）驗中得到（dào）了（le）較好的驗證。李翔龍[13]提出了一種基於進化神經網絡的電（diàn）極損耗預測補償方法，反映出了電火花加工的規律。裴景玉[14-15]針對電火花銑削加工，建立了型腔加工底麵輪廓的數學模型， 並提（tí）出了微細電火花銑削的定長補償加（jiā）工方法，實現了加工的實時補償，提高了（le）尺寸精（jīng）度（dù）和形狀精度。
 
      利用定（dìng）長補（bǔ）償方（fāng）法進行電火花銑削加工，再配合電極旋轉（zhuǎn），電（diàn）極會逐漸形成穩定的（de）圓錐形[16]。而三維型腔（qiāng）的電火花銑削采用分層加（jiā）工的方法，每層分兩步進行，錐形（xíng）的特征會導致在第一層加工後型腔底麵形成一道道（dào）殘餘凸起組成的不平整麵，破壞了定長補償模（mó）型初始加工麵為平麵的條件。因此如何解決在不平整麵上繼續采用（yòng）定（dìng）長補償方法（fǎ）進行平
麵加工就顯（xiǎn）得尤為關鍵。本文對（duì）電火花（huā）銑削加工型腔（qiāng）的一層殘（cán）餘底麵形貌（mào）進行研究，分別建立了三角形仿真（zhēn）模（mó）型和正弦型仿真模型模擬底麵輪廓，通過改變相應參數，對型腔一層最佳表麵（miàn）的獲取及（jí）影響因素（sù）進行探討，得出了相應規律，為後續（xù）第二層及整個型（xíng）腔加工提（tí）供了理論參考。
   
       2 、基於錐形（xíng）電極定長補償加工方（fāng）法
 
      如圖（tú）1 所示，在電火（huǒ）花加工（gōng）中，電極按預定軌跡y=g（x）在工件表麵加工，但由於電極在加（jiā）工（gōng）過程（chéng）中存在（zài）電極損耗，使實際加（jiā）工出（chū）的底麵為H（x），其中y=G（x）表（biǎo）示工件待加工表（biǎo）麵。

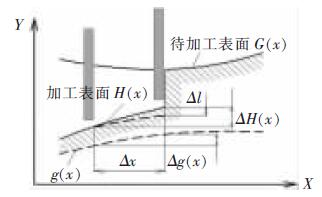
                 圖1 電火花（huā）銑削加工底麵輪廓變化示意圖

      定長補償方法被用來（lái）彌補在電加（jiā）工過（guò）程中因電極的損耗引（yǐn）起的底（dǐ）麵不（bú）平整。如圖2 所示，其加（jiā）工過程（chéng）可分為3 個部分，分別為電極做垂直於工件表麵的打孔加工、水平的銑削（xuē）加工以及再次垂直於工件（jiàn）表（biǎo）麵的補償加工。HW稱為加工中的初始分層厚度，水平運動距離L 稱做補償長度，le稱為該方（fāng）法的補償精度。
 

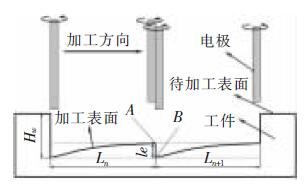
                     圖2 電火花銑削定（dìng）長補原理圖
     
     3 、基於定長（zhǎng）補償的微細型腔加工方法
 
     3.1 型腔第一層加工
    
     三維型腔的電火花銑（xǐ）削采（cǎi）用分層加工的方法，用定長補償法配合旋（xuán）轉， 電極會形成穩（wěn）定（dìng）錐（zhuī）形（xíng），為減小其對底麵波動造成的影響，利用該方法（fǎ）加工型腔（qiāng）第一層分為3 個步驟。如圖（tú）3a 所示，首先，對加工工件進行預加工處理，即為沿著需加工型腔（qiāng）的最外沿進行一圈加工，這樣再進行後（hòu）續的交替（tì）變向加（jiā）工時就不會出現未加工的殘留部分；第二步進行連
續變方向交替加工（gōng）， 以無（wú）軌跡重疊的方式進行加工；第三步是將第二步加工殘餘鋸齒麵中三角凸起的中心連續線作（zuò）為銑削加工的加工軌跡。白色的點表示加工起點，黑色的點表示加工終點。
 

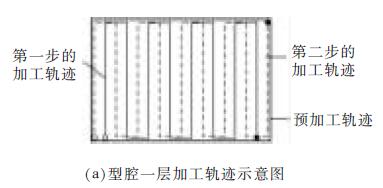
                           圖3 型腔第一層加工（gōng）圖

    圖3b 是經兩（liǎng）步加工後得到的加工底麵顯（xiǎn）微照片，可看出，原來第一步的加工底部的痕跡仍存在，同時第二步的加工是在第一步的兩道（dào）相鄰（lín）的加工軌跡中間進行的。所以原來第一（yī）步加工留下的三角形凸起，現在就變成了第二步加工的加工痕跡。
 
    3.2 一層殘餘底麵對二（èr）層加工影響的仿真（zhēn）研究
 
    利用定長補償方法加工型腔一層後會（huì）留下波浪狀的加工表麵（miàn），破壞了定（dìng）長補償初始加工表麵為（wéi）平（píng）麵的模型，因此需對初始加工表麵為波（bō）浪麵的（de）情況（kuàng）下， 上節中提（tí）出的銑削策略依舊適用進行驗證。為了簡化模型，建立了如圖4 所示的正弦函數模擬（nǐ）加工表麵（miàn）。α 表示電極端麵三角形的底角，d 表示電極直徑，HW表示分層厚度，σ 表示放電間隙。

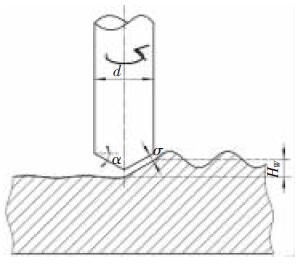
           圖4 圓錐形電極加工波浪狀表麵的示意圖

     基於電火花加（jiā）工通用的理論模型[17]，結合圖1，將工件的待加工表麵（miàn）用方程y=G（x）表示，棒狀電極按照y=g（x）的軌跡加工，實際加工出（chū）的底麵為H（x）。這裏擬建立加工非平麵的圓錐形電極（jí）加工的數學模型。定義（yì）待加工的波浪麵的中間位置和加工後的小波浪麵的中間位置的距離（lí）為加工深度HW，並定義這（zhè）裏的深度為帶有符號的，其值為負數。
 
     仿真的建立基（jī）於以下兩點假設：
 
    （1）加工深度為HW的波浪麵形成的錐形電極的角度與加工平麵的錐形角（jiǎo）度相同，不考慮加工（gōng）中圓錐形角度的變化。
    （2）加工後底麵的（de）波動很小，遠小於待加工麵的波動量。
 
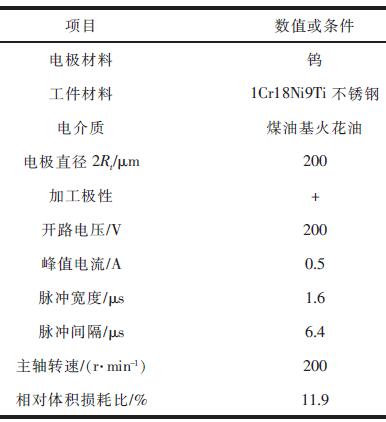
     基於以上假設（shè）及幾何分析，采用MATLAB 方（fāng）法仿（fǎng）真，仿真過程中使用的加（jiā）工參數見表1。

                                   表1 加工參（cān）數表
  
    
   
     仿真結果見圖5。由圖5a 可看出（chū），當加（jiā）工麵為平麵時（shí），采用定長（zhǎng）補償加工型腔完畢後（hòu），底麵輪廓存在的波動為1 μm， 此為機床的最小的加工（gōng）精度值；圖5b 中，當加工麵為波動較小的波浪麵時，設定此時初始波浪麵波動值為20 μm，銑削完畢後底（dǐ）麵輪（lún）廓不平整波動值為1.8 μm；圖（tú）5c 中，當加工麵為波動較大的波浪麵， 此時波動值為40 μm 時，加工（gōng）後底麵輪廓不平整波動值為2.2 μm；而實際實驗中第一層（céng）加工完畢後形（xíng）成的波浪麵的波動幅值約（yuē）為30 μm，即加工得（dé）到的相（xiàng）對應的底麵輪廓波動值（zhí）約為2 μm。
 

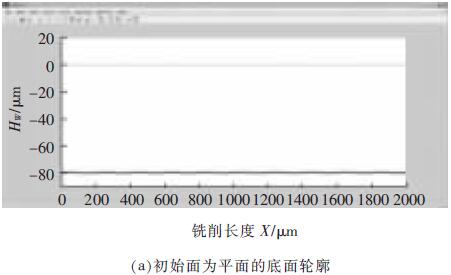
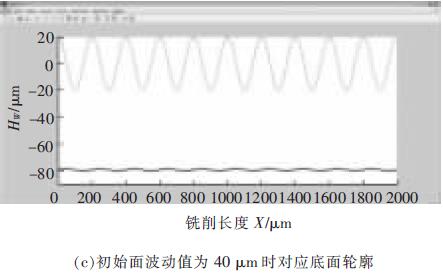
                          圖5 初始麵為不同（tóng）表麵對底麵輪廓的影響仿真圖
   
     3.3 獲取（qǔ）第二步理想分層厚度的方法
 
     由3.2 節仿真結果可得出結論（lùn）： 上一層加工後形成的波浪麵初始表麵對下一層繼續使用定長補償方法進行銑削（xuē）加工型腔底麵的幾乎不（bú）產（chǎn）生影響。這對研究第一層第一步加工後形成的波浪麵尤（yóu）為重要。盡管波浪麵作為初（chū）始加工表麵並不影響接下來多（duō）層銑削（xuē）的底麵平整度（dù），但對於波浪麵的波動量（liàng）仍需進一（yī）步研究（jiū），盡可能使其所形成的（de）底（dǐ）麵在深度尺寸及（jí）平整度方（fāng）麵達到（dào）實（shí）驗預期。

     利用定長補償方法加工型腔，在第一層加工之後會形成如圖6a 所示的底麵輪廓。傳統意義上的最佳表麵為不平整表麵的兩波（bō）峰或兩波穀之間的（de）距（jù）離最小，即（jí）圖6b 所示①、②、③等3 處麵積分別相等。雖然這樣的表麵減小了幾何形狀誤差，卻給定長補償方（fāng）法分層厚度的計算和程序的編寫帶來麻煩。實驗中，將一層加工後底麵變換成（chéng）一個統計意義上的平麵，此平麵的（de）特征為：在（zài）一個虛擬的統計平麵之上（shàng）的殘切工件體積，與虛擬的統計平麵之下的過切工（gōng）件體積相等，即（jí）分層線上下應該滿足關係式①與（yǔ）②的麵積之和（hé）等於③的麵積。此時認為該深度為第二步加工的最佳深度值（zhí）。
 

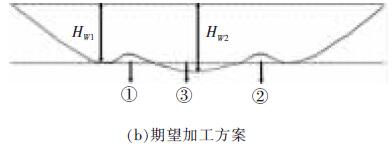
                        圖6 加工底麵輪廓（kuò）共聚焦（jiāo）顯（xiǎn）微鏡檢測圖

     如（rú）圖7 所示，第一步加工後的殘餘底麵為不規則表麵，無法通過計算準確獲取第二步加工的分層厚度。通過設置輔助線可清晰看出，第（dì）一步加工後的殘餘輪廓線介於三角形和同幅同半周期的正弦曲線之間，並依此得到第一層第二步（bù）加工的最佳分層（céng）厚度區間。
 

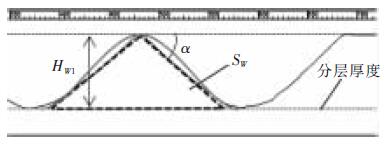
                               圖7 加工底麵殘餘輪（lún）廓
   
     4 、實驗（yàn）及結果
 
     4.1 實驗安排
 
     通過上節的仿真（zhēn）及分析可知，一層殘餘底（dǐ）麵對二層的加工並無影響，所以（yǐ）能找到第一層第二步的最佳分層厚度是後續加工的關鍵所在。經計算，在實際加工中，當第一步加工深（shēn）度為HW1=34.3 μm，即第一步加工補償長度為L1=60 μm 時， 通過三角形假設和正弦曲線假設得到的第二步最佳分層厚度取值區間為HW2=44~52 μm。為了進步細化區間並（bìng）提高效（xiào）率，本實驗采用平行加工3 道槽的簡化方法模擬型腔加工，實驗設備和加工參數（shù）見表2 和（hé）表（biǎo）3。
 
                                           表2 實驗（yàn）儀器
      
  

                                            表（biǎo）3 加工參數

      
  
  
       首先電極在X 軸方向上進行兩（liǎng）道平行槽的加工，槽間距為兩倍放電間隙。然後將電極移（yí）動到兩道加工軌跡的中間，進行第一層（céng）第三道的定長補償加工，補償長（zhǎng）度為L2。在44~52 μm 內以2 μm 為間隔，取（qǔ）5 個不同的補償長度L2進行重複實驗，以觀察所獲得的底麵是否符合統計平麵的特征。
 
      4.2 實驗結果
   
      利用共聚焦顯微鏡生成的加工截麵（miàn）輪廓見圖8。測量時忽略底麵（miàn）輪廓深度的過渡段，直接在穩定階（jiē）段對應的部分分為3 個采樣點進行測量，在加工長（zhǎng）度達到（dào）2 mm 時，加工達到穩（wěn）定段。因此（cǐ），加工槽上測量點選加工長度為2.5、3、3.5 mm 處分別多（duō）次采樣進行測量並求取平均值。
 

                                      圖8 加工截麵輪廓圖
 
     在不同的采樣點處（chù）得到分層線上下區域的截麵圖後， 分別得到（dào）分層（céng）線上下的兩部分區域的麵積，利用（yòng）MATLAB 圖像（xiàng）處理方法求取分層線上麵區域的麵積（jī）和與分層線下區域的麵積的（de）比值，比值越接近1，則表示此時對應的深度值（zhí）越接近最佳深度，計算結果見表（biǎo）4。

     由表4 可看出， 當第二步加工深度為46 μm時（shí），上（shàng）下區域麵積的百分比為86.48 %，最接近100%，受加工機床精度所限（xiàn），很難再對所分加工（gōng）區間進（jìn）行細化，因此認為此時（shí）為最佳的加工深度，也即用此深度作為第二步加工時的分層厚度進行銑（xǐ）削；當分層厚度為44 μm 時（shí），上下麵積比值大於100 %的值，因此最佳深度的真實值應介於44~46 μm 之間；另一方麵，從表格數據可看出，上（shàng）下麵積（jī）比對加工深（shēn）度敏感，深度的微（wēi）小變化即（jí）給麵積（jī）比造成很大（dà）影響，也（yě）為進一步的（de）區（qū）間細化帶來難度。
   
                                           表4 測量及計算結果
    
   
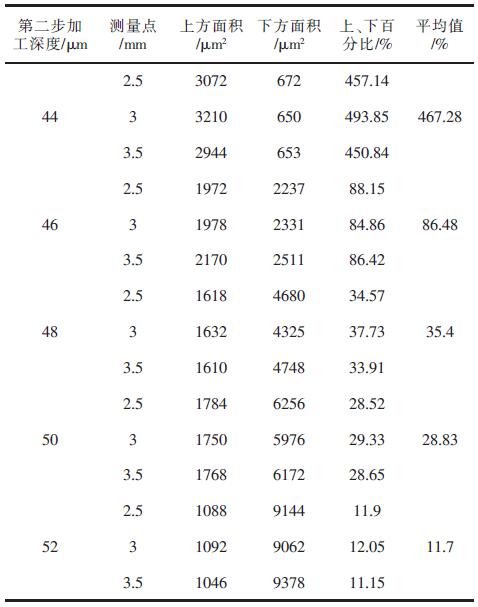
     圖9a 為顯微鏡下的加（jiā）工槽實物圖，圖（tú）9b 為對應圖9a 豎線標記處的截麵（miàn）輪廓圖。可（kě）看（kàn）出，加工（gōng）深度為46 μm 時，對應的底麵輪廓分層線上、下區域的麵積（jī）基本相（xiàng）等（děng），達到了統計意義（yì）上的平麵。
 
     5 、結論（lùn）
 
    （1）在采用定長補償法的電火花銑削過程中，配合電極旋轉，電極（jí）端麵會形成圓錐形。
    （2）利用定長補償法加工三維型腔，會在一（yī）層加工後形成波浪狀不平整表麵，破壞（huài）了該方法初始加工表麵為（wéi）平麵的模型。針對波浪麵對加工底麵的影響進行了仿真分（fèn）析，結果表明波浪麵對最終的型腔底麵形狀（zhuàng）幾乎不產生影響。
 

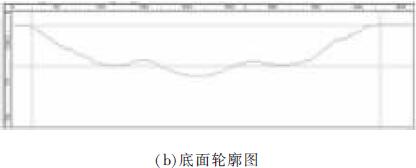
                             圖9 加工深度為46 μm 時的底麵輪廓（kuò）圖

     （3）為達（dá）到統計意義上的平麵，確定了第二步加（jiā）工的最佳深度（dù）的（de）定義；並通過三（sān）角形假設和正弦曲（qǔ）線假設從幾何上找到了最佳深度的取值範圍。
     （4）針對最佳深度值的獲取進行了理論分析計算（suàn）及實驗探究， 結果表（biǎo）明當分層厚度為46 μm 時，上下（xià）麵積最為接近，初定為最佳的分層厚度，而真實的最佳深度值介於44~46 μm 之間。