摘要:機床剛度、固有頻率等動力學特性隨著機床部件位置、姿態在工作(zuò)空間中的變(biàn)化而變化。對機床(chuáng)動力學特性的(de)研究不僅需要考慮到機床質量、剛度、阻尼(ní)值的(de)大小,還應重視(shì)機床加工(gōng)點的空間位置變化。采用空間統計學方法,以超精(jīng)密機(jī)床固有頻率這一關鍵動力(lì)學性能(néng)為例,分析機床(chuáng)動力學性能(néng)與機床位(wèi)置姿態之間的(de)數學關係,選(xuǎn)取機床動態特性變異(yì)函數,建立動力學性能變化預(yù)測的Kriging 方法模型,研(yán)究(jiū)動力學特性在工作(zuò)空間中的變化規律以及動力學特(tè)性空間信息的表述(shù)方法(fǎ)。將所建立(lì)的模型與正交(jiāo)多(duō)項(xiàng)式方法、徑向基神經網絡方法、二階響應(yīng)麵方法等方法建立(lì)動力學性能預測分析模型比較(jiào),空間統計學Kriging 方法(fǎ)所建立的模型R2 檢驗大於0.96,在四種模型建構(gòu)方式中為精(jīng)確度(dù)最優,能夠在完整(zhěng)工(gōng)作空間中準確地描述機床動力學特性(xìng)。基於空間統計學的機床動力學特性研(yán)究為機床的動力學設計提供了新的設計分析方法及相應的技術支持。
關鍵詞:機床動力學;加工空間;空間統計學(xué);Kriging 模型;固有頻率
0 前言
機床動力學特性是機床(chuáng)重要的性能指標。不(bú)恰當的機床(chuáng)設計(jì)和使用將(jiāng)引起機床加(jiā)工中的顫振,使得機床(chuáng)的切削條件變(biàn)得不穩定,導致刀具(jù)的磨損和斷裂,產生加工中的振動和噪聲,影響機床加工精度和工件表麵形貌,加速機床本身(shēn)的磨損和破壞。與機床(chuáng)動力學(xué)性能相關的機床設計參數通(tōng)常(cháng)有機床的(de)剛度、固有頻率、模態振型(xíng)、阻尼、質量分(fèn)布等。機床動力學特性(xìng)設計和分析通常采用有限元(yuán)方法建(jiàn)立虛擬仿真環境[1-3],提供在一個具(jù)體的位置(zhì)和姿態下(xià),機床的n 階(jiē)固(gù)有頻率和對應的(de)模態振(zhèn)型以及剛度(dù),為機(jī)床的動力學設(shè)計提供數據支持。虛擬(nǐ)仿真環境解決了機床運動過程中(zhōng)的位置相(xiàng)關的(de)動力學性能評估問題,但尚未對機床(chuáng)各加工位(wèi)置之(zhī)間的動力學性能的(de)變化趨勢和關聯性進行(háng)分析。針對機床工作空間中動力學特性的演(yǎn)變,許多學(xué)者進行了(le)分析研究。ZAGHBANI 等[4]采用機(jī)床加工過程中模態的變化為指標來評估(gū)機床動力學特性的穩定性。WU 等[5]分別使(shǐ)用數值計算和試驗方法研究了5自由度混聯機床工作空間中的(de)剛度分布,並嚐試通過改(gǎi)進剛度最低的部件(jiàn)剛度來優化係統剛度。劉海濤(tāo)等[6]通過定義廣義加工空間函數的(de)方法,在龍門(mén)機床和立(lì)式機床的整個工作空間進行(háng)模態分析和動(dòng)力響應分析,獲得了低階固有頻率在加工空間中變化最(zuì)大可達25%的結論,證明了機床性能的優化中完整模態(tài)信息的重要性(xìng)。但目前,關於動(dòng)力學特(tè)性在工作空間(jiān)中的變化規律的研究以及動力(lì)學特性空(kōng)間信息的表述方法的研究還未見有詳細研究的報導。
本文通過機(jī)床(chuáng)工作空間動力(lì)學特性(xìng)分析機床動力學性能的空間特性的內在形成機製,繼而,以一階固有(yǒu)頻率為例,建立空間中的機床動力學特性的空間統(tǒng)計學模型,通過與(yǔ)正交多項式模型、神經網(wǎng)絡模型及二次響應麵模型(xíng)的比(bǐ)較,分析動力學性能的影響因素的同時,獲得高精度的空間動力學特性表征模型。
1 、機床動力學性能(néng)的空間特性分析
如圖 1 所示[7],機床剛度、固有頻率、模態振型等動力學參數是機床(chuáng)關鍵部件及(jí)結合部組成的(de)剛度鏈[8-10]結構特性和機床空間位置、姿態等空(kōng)間特性的函數。剛度鏈隨著機床(chuáng)的位姿變(biàn)化而變化。剛度鏈每一位置姿態對應的剛(gāng)度、固有頻率等模態(tài)信息都可以使用多體動力學和有限元分析的聯合仿真方法求解[2]。
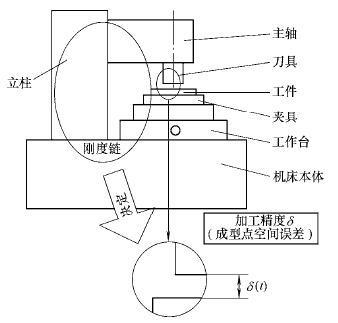
圖(tú)1 機床(chuáng)剛度(dù)鏈及機床動(dòng)力學特性(xìng)
機床剛度鏈(liàn)的兩個端點(diǎn)刀具和工件在加(jiā)工過程中位置變化包絡形成機床工作空間。加工空間內的質量矩陣(zhèn)、阻尼矩陣、剛度矩陣隨著機床位置姿態的變化而變化,並引起固有頻率、模態、動剛度等動態特性的變化。其中,質量矩陣在加工(gōng)過程中隨著運動部件重心的變化而變化;阻(zǔ)尼產生機理和計算方法(fǎ)尚有爭論;機床的剛度鏈組成(chéng)複雜,包括:結構件(jiàn)剛度、主軸剛度、導軌(guǐ)剛(gāng)度、結合部剛度、電機伺服剛度、氣浮軸承剛度等,在機床運動過程中,這些剛度(dù)鏈的剛度變化(huà)量級不(bú)同。在三個因素綜合作用下,機床的固有頻率、模態、動剛度(dù)等動態特性在加(jiā)工空間中的(de)變化呈現非線性、變化規律複雜。
決定機床動力學特性的機床質量矩陣 m、剛度矩陣k 和阻尼矩陣c 都隨著剛度鏈的變化而變化,機床的動力學特性是(shì)空間位置(x, y, z)的函數。可寫為(wéi)

將位置姿態(tài)數據(x, y, z)反複代(dài)入到(dào)式(1),獲得某5軸銑床各加工位置(zhì)的一階固有頻率,如圖(tú)2 所示(shì)。對式(1)、(2)進行模態疊(dié)加,可得到由固有頻率值和模態矢(shǐ)量表述的動剛度等動(dòng)態特性

根據以上(shàng)數學推導及分析可知,由於機床運動中質量、阻尼、剛度改變的連續性,加工空間中的動力學(xué)特性數據各(gè)位置間明顯具有關聯(lián)性,表現為鄰近位置的動力學特性相似。這種數據之間的關聯性,使得超精密機床加工空間動態性能具有空間依賴(lài)性(空(kōng)間自相關)。在進行動態性能分析時,既考慮到各(gè)采樣點具體值的(de)大小(xiǎo),又重視樣本空間位置及樣本間的距離(lí)的方法會更有利於動態(tài)性能的把握。空間對(duì)象間的相關性和非(fēi)獨立的有效科學方法是基於數據的空間統計學。從(cóng)這個性質而言,傳(chuán)統的代(dài)數多項式擬合建立在數據獨立性的基礎上,代數多項式的統計模型對空間數據的分析會產生虛假的解釋。目前流行的神經網絡方法沒有在算法中明確指出從(cóng)空間特性上對動態性能學習和分析的途徑,其對整機動態特性的掌握也沒有考慮空間數據關係(xì)的(de)空間分析方法精準。在空間特性分析上,Kriging 方法[11-12]是以已知樣本信息(xī)的動態構造為基礎,充分考慮到變量在空間上的相關特征,建立對象(xiàng)問題的近似函數關係來模擬某一點的(de)未知信息的有效空間統(tǒng)計學方法。
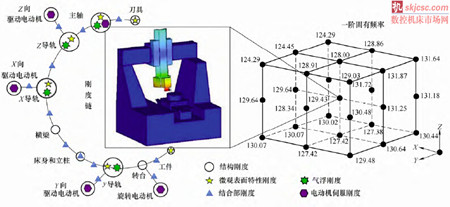
圖2 加工空間各加工位(wèi)置的固有頻率值
因此,本文(wén)嚐試使用 Kriging 方法建立近似模型對加工空間(jiān)動態特性預測分析,並與傳統代數多項式建立的(de)響應麵近似模型、及基於對數據學(xué)習(xí)分析的神經網絡模型對比,以期獲取更好性能預測(cè)分析(xī)。
2 、動力學(xué)性能的Kriging 預測模型
Kriging 插值[11]是一種求最優、線性、無偏的空間內插(chā)方法,采用協方差衡量各點空間相關程度。它是基(jī)於(yú)線性回歸分(fèn)析的一種改進,模型包含了線性回歸部分和非參數部分,其中的非參數部分被稱為變異函數,采用隨機分布函數的(de)實現。
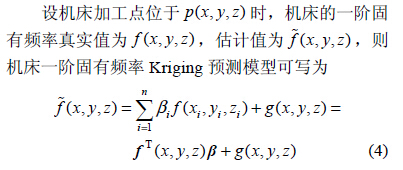

常用於擬合變異函數的模(mó)型包括指數模型、高(gāo)斯模型、Matérn 線性模型、Matérn 立方模型。通過計算模型協方差,找出最佳(jiā)理論變異函數模型,獲得最好擬合效果,計算公(gōng)式為(wéi)
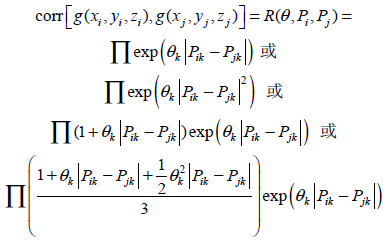


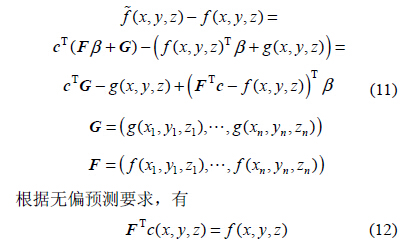
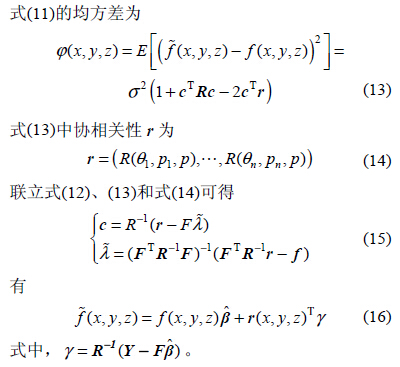
至此,對加工空間中任意點的一階固有頻率可使用式(16)計算獲得。其他如剛度、高階固有頻率、阻尼等相關動態性能(néng)參數(shù)均可使用此方法計算。下麵以(yǐ)一階固有頻率為例對Kriging 方法建(jiàn)立的(de)模型(xíng)進行加工空間內機床動態特性(xìng)分析。
3 、機床動態特性分析
3.1 動態特性變異函數的選擇
取圖 2 中27 個空(kōng)間點作為位置變(biàn)量輸(shū)入P = {p1, p2 ,, pn},對應響應變量的輸出數據f1,f2.... fn,計算刀具加工點(diǎn)位於空間位(wèi)置p 時機床的動態性能。
將(jiāng)已知的 27 個空間位置的一階固有頻(pín)率數(shù)據代入,選擇(zé)變異函數(shù)g(x, y, z)協方差計算模型為指數模型,獲得正則化θ 參數如表1 所示。
表 1 Kriging 模型(xíng)θ 參(cān)數

至此,完成整體模型擬合。



圖3 指數函數模型頻率預測(cè)值與真實值比較由於 Kriging 模型建立時考慮了數據的內在相關性,所有變異函(hán)數獲得的近似模型擬合精確(què)度檢驗R2 檢驗值均大於0.95,四種(zhǒng)變異(yì)函數都可以比較精確地表達一階固有頻率在加工空間內的變化規律。四種模型中指數函數模型能夠更好地表達(dá)數據之間的相關性(xìng),近似精度最高。
3.2 一階固有頻率的變(biàn)化規律(lǜ)
以圖 2 中(zhōng)的超精密銑床為例,研究機床加工空間中一階固有頻(pín)率的變化規律。
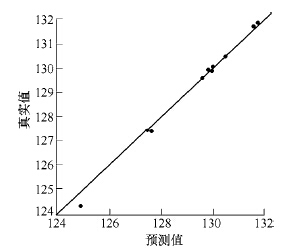
圖3 指數函數模型頻率預測值與真實值比(bǐ)較(jiào)
圖 4 中X 剖麵從左到右依次為x=-115 mm,x=0mm,x=115 mm。對三幅圖中同一(y, z)點值(zhí)分析可知,隨著導軌在X 方向的移動,該超精(jīng)密銑床工作空間中相同(y, z)位(wèi)置一階頻率將產生6%非線性改變。圖 5 中Y 剖麵左到右(yòu)依次為y=0 mm,y=112.5mm,y=225 mm。對三幅圖(tú)中同一(x, z)點值(zhí)分析可知,隨(suí)著導軌在Y 方向的移動,工作(zuò)空間的相同(x,z)位置一階頻率幾乎沒有發生改變。由(yóu)此(cǐ)可知,能(néng)通過Y導軌運動到達的工作位置,應優先移動Y導軌。如圖 6 所示,圖中(zhōng)Z 導軌位置從左(zuǒ)到右(yòu)依次為z=0 mm,z=80 mm,z=160 mm。隨著導軌在Z 方向的(de)移動,工(gōng)作空間中相同(x, y)位置一階頻率將產生(shēng)5%的非線性的改變。由於Z 方向是加工敏感方向,這種變化(huà)在超精密加工中產(chǎn)生影響需要盡量避免。對(duì)三幅圖中同一點值分析可知,當Z 導(dǎo)軌位於定導軌中部(z=80 mm)位置時(shí),工作空間中(x, y)點位置的變化對整(zhěng)機頻率影(yǐng)響最小。
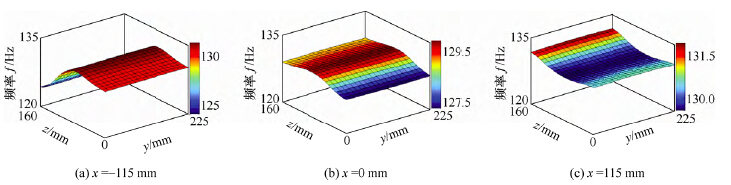
圖4 工作空間內的一(yī)階(jiē)頻率(X 剖麵)
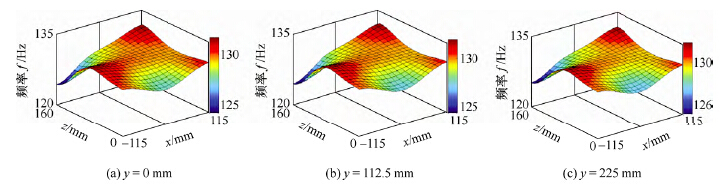
圖5 工作空間內的(de)一(yī)階頻率(lǜ)(Y 剖麵)
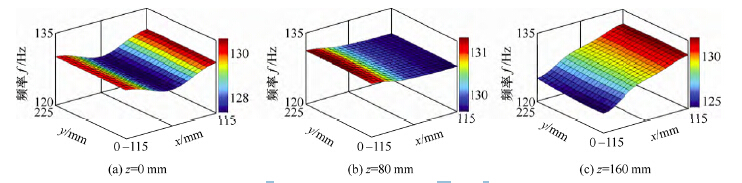
圖6 工作空間(jiān)內的一階(jiē)頻率(Z 剖麵)
根據以上分析可知,機(jī)床的一階固有頻率在工作空間是變化的,為了保持機(jī)床(chuáng)工作的平穩,應優先使用頻率變化小的運動方式來保(bǎo)障機床具(jù)有更(gèng)平穩的動態性能。以(yǐ)文中所使用的(de)超精密銑床(chuáng)為(wéi)例,該機床在工作時應該盡量使(shǐ)得Z 導軌停留在定導軌的中部,優先進給(gěi)Y 軸,減(jiǎn)少X 導軌的運動來降低超精密加工中機床性能變化對精度帶來(lái)的不利影響(xiǎng)。
4 、對比研究
機械設計分析中,傳統上更多地使用包括正交多項式模型(xíng)[14-15]和響(xiǎng)應麵模型(xíng)[16-17]等多項式近似模(mó)型。近年來,神經網(wǎng)絡模型[18-19]作為近似分析模型在(zài)機床建模和機械產品性能分析中也日益廣泛使用。本節測試這三種模型在機床動態特性分析中的適(shì)用性(xìng)。
4.1 正交多項式模型
將 上 述 27 個采樣(yàng)點(diǎn)作為輸入點, 采用(yòng)CHEBYSHEV 正交多項式建立機床一階固有頻率的空間動態模(mó)型。可(kě)解得R2=0.471 63,由於R2 小於0.9,誤差值過大,這種算(suàn)法構建的一(yī)階固有頻率空間變化規律模型用於分析時可信度非常低。
計算出的一階固有頻率(lǜ)預測值與真實值比較(jiào)及一階固有頻率(lǜ)分布如圖(tú)7、圖8 所示(shì)。由於誤差值(zhí)過大,可認為這種構(gòu)造近似模(mó)型的方法得到的近似模型用於分析時可信度(dù)較低。
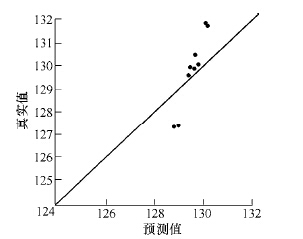
圖7 正交多項式近似模型頻(pín)率預測值與真實(shí)值比較
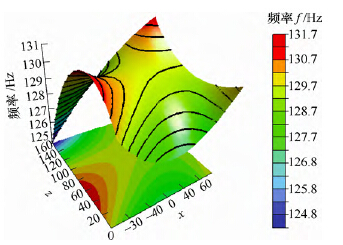
圖8 正(zhèng)交多項式(shì)近似模型仿真結果
4.2 徑向基神經網絡模型
徑向基神經網絡模型形參(cān)數取值 2.97,構造後得到R2=0.885 47。殘差分析(xī)如圖9 所示(shì),仿真模型如圖10 所示。由於誤差值過大(dà),可認為這種構造近似模型的方法得(dé)到的近似模型用(yòng)於分析時可信(xìn)度較低。
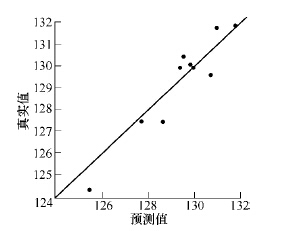
圖9 神(shén)經網絡模型模型頻率預測值與真實值比較
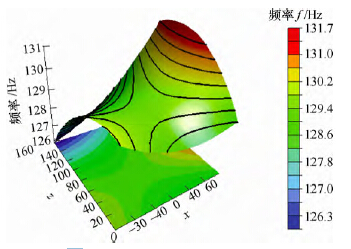
圖10 神經網絡模型(xíng)仿真結果及分析
4.3 二階(jiē)響應麵模型
根(gēn)據給定的 27 個點的初值,可寫出二階響應麵模(mó)型(Response surface method, RSM)構造方程。二階(jiē)響應麵模型R2=0.346 71,精確度分析如圖11 所示,頻率分布仿真(zhēn)效果如圖(tú)12 所示。由於R2 遠小於0.9,誤(wù)差值過大,可認為這種構造近(jìn)似模型(xíng)的方法得到的近似模型用於分析時可信度非常低(dī)。
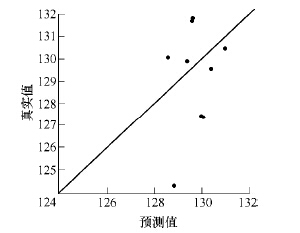
圖11 RSM 近似模型頻率預測值(zhí)與真實值比較(jiào)
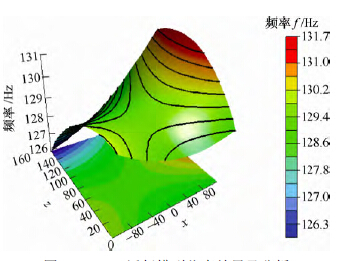
圖(tú)12 RSM 近(jìn)似模型仿真結果及分(fèn)析
5 結論
(1) 本文使(shǐ)用Kriging 方法(fǎ)建立空間(jiān)統計模型進行機(jī)床動力學特性研究,獲得了固(gù)有(yǒu)頻率、剛度在加工空間分布規律,在完(wán)整工作空間中準確的描述超精密機床動力學特(tè)性。
(2) 機床動力學特性的(de)剛度、固有頻率等主要因素隨著機床位置(zhì)姿態的變化規律可使(shǐ)用Kriging方法描述。方法中的四種變異函數模型(指數函(hán)數、高斯函數、線性函數、三次函數(shù)),指數(shù)函數模型能夠更好的表達數據之(zhī)間的相關性,近似精度最高。
(3) 由於正交多項式模型、響應麵模型和神經網絡模型在模型建(jiàn)構中使用了數據獨立性假設,該假設與機床動態特性數據的空間相關性相違背,所以不適合用於(yú)機床動(dòng)力學特性變化(huà)規律的描述。本文的(de)研究結果為(wéi)超精密(mì)機床的動力學設計提供(gòng)了新的設計分析(xī)方法和技(jì)術支持。為機床使用中加工位置和(hé)姿態的選擇(zé)和路徑規(guī)劃提供了原理和數(shù)據支(zhī)持。
如果您有機床行業(yè)、企業相關新聞稿件發表,或進行資訊合作,歡迎(yíng)聯(lián)係本網編輯部, 郵(yóu)箱:skjcsc@vip.sina.com
- 2024年11月 金屬切削機床產量數據
- 2024年11月 分地區金屬切削機床產量數據(jù)
- 2024年11月 軸承出(chū)口情(qíng)況(kuàng)
- 2024年11月 基本型乘用車(chē)(轎車)產量數(shù)據
- 2024年11月 新能源汽車產量(liàng)數據(jù)
- 2024年11月 新能源汽車銷量情況
- 2024年10月(yuè) 新能源汽車(chē)產量數(shù)據
- 2024年(nián)10月 軸承出(chū)口情況
- 2024年10月 分地區金屬切削機床產量數據
- 2024年10月 金屬切削機床產量數據
- 2024年9月(yuè) 新能源汽車銷量(liàng)情況
- 2024年8月 新能源汽車產量數據
- 2028年8月 基本型乘用(yòng)車(轎車)產量數據
- 機械加工過(guò)程圖示
- 判(pàn)斷一台加工(gōng)中心精度的幾種辦法
- 中走絲線(xiàn)切割機床的發展趨勢
- 國產數控係統和數控機(jī)床(chuáng)何去(qù)何從?
- 中國的技術工人都去哪裏了?
- 機械老板做了十多年,為何還是小作坊?
- 機械行業最新(xīn)自殺性營銷,害人害己!不倒閉才
- 製造業大逃亡(wáng)
- 智能時(shí)代,少談點智造,多談(tán)點製造(zào)
- 現實麵前,國人(rén)沉默。製造業的騰飛,要(yào)從機床
- 一文搞(gǎo)懂數控車床加工刀具補償功能
- 車床鑽孔攻螺紋加工方法及工(gōng)裝設計
- 傳統鑽(zuàn)削與螺旋銑孔(kǒng)加工工藝的區別




