振動驅動移動機器人（rén）直線運動的滑移分岔-機器人-數控機床市場網

您現在的位置：機器人（rén）> 技術前沿>振動驅（qū）動移動機器人直線（xiàn）運動的滑移分岔

振動驅動移動機器人直線運動的滑移分岔

2017-3-1 來源：同濟大學航（háng）空航天與力學學院作者：陳祺占雄徐鑒

摘（zhāi）要:近年來，隨著移動型機器人設計技術水（shuǐ）平（píng）的不斷提高，其運動形式日趨多樣. 借助於仿生學的思想，模仿蚯蚓等動物的蠕動成為不少機器人設計者（zhě）所追求的目標. 為了實現這（zhè）一目標，學者們提出並研究了振動（dòng）驅動係統. 本文研究了各向同性幹（gàn）摩擦下，單模塊三相振動驅動係統的粘滑運動. 考慮到庫倫幹摩擦力的（de）不連續性，振動（dòng）驅動係統屬於Filippov 係統. 基於此，運用Filippov 滑移分（fèn）岔理論，分析了振動驅動係統不同的粘滑運動情況（kuàng）. 根據驅動參數的（de）不同，係統運動的滑移區域被分成4 種基本情形（xíng）. 對這些情形分類討論（lùn），得到係統的6 種運動情況. 然後對這6 種運動情況進行歸納（nà），最終得出係統一（yī）共存在4 種不同的粘滑運動，而（ér）且也解析地給出了發生這4 種（zhǒng）粘滑運動的分岔條件. 分岔條件包含係統的3 個驅動參數（shù），通過變化這些參數，得到了係統運動的分岔（chà）圖. 借助分岔圖，詳細分析了隨著（zhe）驅動參數的變化，係（xì）統如何（hé）實現不同粘滑運動類（lèi）型之間的切換，並從（cóng）分岔角度給出了相應的物理解釋. 最後，通過數值方法直接求解原運動方程（chéng），數值解法得到的4 種運動圖像與理（lǐ）論分析一致，驗證了係統運動（dòng）分岔研究（jiū）的正確性.

關鍵詞:振動驅動係統，三相驅動，各向同性幹摩擦，分（fèn）岔

0.引言

眾所周知，蚯蚓等軟（ruǎn）體動（dòng）物通過蠕動實現運動，這種運動形（xíng）式看似簡單（dān），卻憑借其（qí）一大優勢——無足，吸引了眾多學者的關注（zhù）[1-6]. 受此啟發，一類新型的運（yùn）動模型——振動驅動係統，近年來得到了廣泛的研究[7-25]. 這種運動模型繼（jì）承了蚯蚓運動的（de）優勢—— 不需要外（wài）部驅動（dòng）部件，如腿或輪子，因此易於（yú）實現結構的微型（xíng）化，密封化. 可以預見，基於振動驅動這（zhè）一思（sī）想的機器人能更好地適應多種環境，甚至有學者期望將其（qí）製成微型膠囊機器人（rén）進入人體腸道甚至血管中治療疾病.

2005 年，Chernousko[7] 研究了兩個質量塊係統的直線運動，通過選擇合（hé）適的物理參數並合理地（dì）控製兩個質量塊（kuài）之間的相互作用力，實現（xiàn）了該係統的最快平均速度. 在此基礎上，其首次提出了由一個內部質量塊和一個外部箱型剛體構成的振動驅動係（xì）統模型[8]. 在該模型中，內部質量塊相對於（yú）外部箱（xiāng）體做周期運動，通過合理設計內部（bù）質量塊的周期運動形式，外部箱體可以在內部質量塊對其作用力以及支撐麵對其摩擦力的共同作用下，實現周（zhōu）期平移運動. 因（yīn）而，對質量塊的相對運動形式進行設計和優化以實現係統最（zuì）大平均速度是（shì）該類係統（tǒng）研究的一個（gè）關鍵問題. 縱觀之前的研究，質量塊的控製模式（shì）大致（zhì）分為兩類：對稱控（kòng）製（zhì）和非對稱控製. 對稱控製意味著內部質量塊的（de）相對運動形式具有對稱（chēng）性，也更容易實現（xiàn），比（bǐ）如正弦驅動，但是往往需要環境提供能使係（xì）統發生剛體位移的異性（xìng）摩擦. 2012 年，Fang 等[9] 在（zài）研（yán）究三模（mó）塊（kuài）振動驅動係統（tǒng）時使用（yòng）了正弦驅動，他們發（fā）現通過（guò）優化各模塊中正弦驅動的初始相位差，能夠有效地提高係統的（de）穩態平均速度. 2014 年，Fang等（děng）[10] 研究了正弦驅動下，單模塊（kuài）振動驅動係統的運動，重點從滑移分岔（chà）的角度分析了係統（tǒng）的粘滑運動，加深了人們對（duì）該類係統粘滑運動的認識. 對稱（chēng）驅動的研究總的來說並（bìng）不如非對稱驅動的研究多. 早在2005 年Chernousko[7] 就提出了兩種非對稱驅動模式—— 兩相驅動和三（sān）相驅動，對實現振動驅動係統的運動都行之有效. 2006 年，Chernousko[11] 研究（jiū）了兩相驅動模式，這（zhè）種驅（qū）動模式下（xià），內部質（zhì）量（liàng）塊一個周期內的相對運動被分為兩段，每段上的相對運動速度均為常數. 以實（shí）現係統的（de）最大穩（wěn）態平均速度為目標，對兩相驅動參數進行了優化. 2007 年，Chernousko[12] 研究了三相驅動下振動驅動係統的運（yùn）動. 該種情形下，內部質量塊一個周期內的相對運動被分為三段（duàn），每段上的加（jiā）速度大（dà）小為常數. 由於（yú）庫倫幹摩擦的存在，以及不同時間域內，內部質量（liàng）塊的相對加速度不同，加上係（xì）統速度的不斷變化，因而係統會（huì）發生複雜的粘滑運動. 2011 年（nián），Fang 等[13] 運用平（píng）均法（fǎ）研究了三相驅動的單模（mó）塊振動驅動係統在不存（cún）在粘滑效應時的速度. 但是（shì）當考慮粘滑效應時，平均法不再適用，根據（jù）粘滑（huá）運動發生情況，係統運動可（kě）以被細分成8 種情況. 2011 年，Fang 等[14] 在研究兩模塊振動驅動（dòng）係統時，在兩（liǎng）個模（mó）塊中也分別施加了這種三相驅動，通過調節兩組（zǔ）振動的相位差實現了（le）係統的較快運動速度. 可見，三相驅動（dòng）在振動驅動（dòng）係統的（de）控製（zhì）中占有重要的地位. 此外，2006 年Li 等[15] 使（shǐ）用的（de）四步驅（qū）動以及2011 年Huda 等[16] 使用的四相驅動也屬於非對稱驅動.

除了上文中內部質量塊的（de）相對運動形式（shì）以外，另外一個對振動驅動係統（tǒng）的運動行為起很大影響的是係統（tǒng）受到的外部摩擦. 2007 年，Chernousko[12] 研究（jiū）了非（fēi）對稱（chēng）黏性摩（mó）擦下（xià）振動驅（qū）動係（xì）統的運動，這種環境模擬（nǐ）了係統在液體環境中的運動. 研究針對振（zhèn）動驅動係統速度進（jìn）行了控（kòng）製（zhì）參數優化，並加以實驗驗證.2009 年，Bolotnik 等（děng）[17] 研究了平方阻尼作用下（xià）係統的運動情況，這種運動常常在係統運動速度較快、雷諾數較大的（de）環境下發生. 研究（jiū）表明，在平（píng）方阻尼作用下，即使是各向同性的阻力，係統也能（néng）實現向前運動. 2011 年，Fang 等[13] 研究了振動驅動係統在非對稱庫倫幹摩擦下的運動情況，由於幹摩擦存在，觀察到了前（qián）麵（miàn）所（suǒ）述的粘滑運動.

事實上，粘滑效應至今為止仍然是振動驅動係統中的一大難題. 一方麵，粘滑效（xiào）應使得運動情況複雜多樣，難以分析（xī），另一方麵，充（chōng）分利（lì）用粘滑效應也是提高係統運動性能的重要措施. 粘滑運動往往都是在庫倫摩擦之下發生，這一點，不僅在振動驅動係統中得到體現，而且在其他係統中也有發現（xiàn）並（bìng）被研究[18;26-28]. 庫倫摩擦之所（suǒ）以能（néng）引起（qǐ）粘滑運動，是因（yīn）為其不連續性. 從運動狀（zhuàng）態場的角度看，這種由摩（mó）擦力引起的（de）不連（lián）續係統，是一（yī）類典型的Filippov 係統[29-30]，而（ér）Filippov 係統最突出的就是利用滑移和滑（huá）移分岔（chà）理論巧妙地分析係（xì）統中的（de）不連續性對運動的（de）影響. 2010 年，Guardia 等（děng）[26]通過滑移分岔理論研究了一個幹摩擦下的彈簧振子，研究證實（shí）係統存在兩參數滑移分（fèn）岔，並得到了其（qí）中一條餘維一分岔曲線的解析表達式. 2007 年，Kowalczyk 等[27] 也通過Filippov 係統（tǒng）模型研（yán）究了幹摩擦下的彈簧振子，發現了係統中的（de）餘維二分岔，並解釋了可（kě）能發生的混沌現象. Filippov 係（xì）統理論為（wéi）研究幹摩擦下的彈簧振子這類係統（tǒng）行為，提供了重要的分析方法[18;26-28]. 受此啟發（fā），2011 年（nián），Fang 等[10] 也利用Filippov 係統描述了（le）非對稱（chēng）幹摩擦下受正（zhèng）弦驅動（dòng）的振動驅動係統，首（shǒu）次從滑移分岔角度闡明了粘滑效應下係（xì）統的運（yùn）動情況（kuàng），優化結果顯示，合理優化係統驅動參數和摩擦係數，能實現係統無後退移動.

回顧（gù）振動驅（qū）動係統十年來的研究[7-25]，無論是內部驅動（dòng）的設計，還是外部阻力的分類，抑或是研究方（fāng）法的選用，都得（dé）到了（le）長足的發展. 值得注意的是，絕（jué）大（dà）部分研究更多地是關注了摩擦力為各（gè）向異性（xìng）時的情（qíng）況，而對於同性（xìng）摩擦的情形（xíng）討論較少. 因此，本（běn）文重點研究了各向同性幹摩擦下的振動驅動係統的運動. 由於摩擦的各向同性，本文中將采用三相驅動這一非對稱驅動以保證係統（tǒng）定向移動的實現. 此外，幹（gàn）摩擦條件下，係統（tǒng）的不連續性會誘發粘滑運動，這種運動的複雜性也對研究工作形成了挑（tiāo）戰. 借助分岔理論可（kě）知，本文中所考慮的振動驅動係統（tǒng）也是Filippov 係統，因此可以從滑（huá）移分岔的角度對係統的運動進行分（fèn）類. 這（zhè）種分（fèn）類有（yǒu）效地揭示了各（gè）向同性（xìng）幹摩擦下振動驅動係統多樣（yàng）的運動行為，對參數的設計起到一定的（de）指導作用. 最（zuì）後（hòu），我們用數值方法對理論分析得（dé）到的運動分類以（yǐ）及運動特性進行了驗證（zhèng）.

1.振動（dòng）驅動係統

1.1 動力學方程

振動驅動係統的基本模型如（rú）圖1 所示. 係統（tǒng）由兩個部（bù）分組成（chéng），分別為質量為M 的剛性箱體以及質量為m 的內部（bù）質量塊. 由（yóu）前人的工作可（kě）知，通過（guò）m相對於M 的特定振（zhèn）動，可以實現係統在水平直線上的定向移動，由此稱其為振動驅動係統. 易知，係統有兩個自（zì）由度（dù），因而可以取兩組獨立的廣義坐標（biāo），

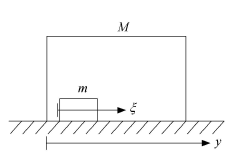
圖1 振動驅動係統（tǒng）

由牛頓第二運動（dòng）定律，可得運動方程

需要注（zhù）意的是，上麵的R(0) 表示速度為0 時，係統所受的摩擦阻力. 因此，如果內部振動提供的驅動力不（bú）足以克服庫倫摩擦，那麽摩擦力就與該力等大反向，維持係統靜止狀態. 如果內部振動提供的驅動力（lì）大於最大靜摩（mó）擦力，那麽係統有運動的趨勢，此時摩擦力的大小就是最大靜摩擦力. 為了（le）簡（jiǎn）便分析，本文中最大靜摩擦（cā）力近似認為等於滑動摩（mó）擦力. 所以有

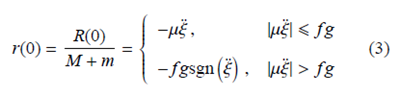
式(2) 和式(3) 是振動驅動的基本力學（xué）模型.

1.2 三相驅動

假設箱體內（nèi）允許質量（liàng）塊（kuài）運動的區間長度為L

三相驅動模式的基本思想是將（jiāng）內部質量塊（kuài）一個周期的相（xiàng）對振動在時間上分為三段，三段區間的長度分別為r1, r2, r3. 並且，在每段時間區間內，質量塊m 相對於M 均做勻變速直線（xiàn）運（yùn）動，由式(5)r 式

(7) 易知，第一、三段（duàn）中m 相對運動的加速度為正（zhèng）常數，第二段中m 相對運動的加（jiā）速度（dù）為負常（cháng）數. 一個周期內，m 相對運動的數學表達式如下

三相驅動模式下內部質（zhì）量塊相對運動圖像如圖2 所示.

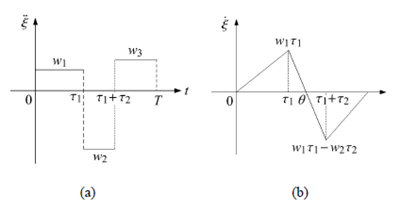
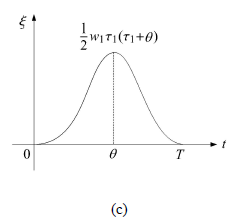
圖2 三相（xiàng）控製模式下m 的(a) 相對加速度、(b) 速度和(c) 位移

三相驅動中，獨立的（de）控製變量有3 個，本文使用wi(i = 1; 2; 3) 作為（wéi）控製的（de）自變量. 當一組wi(i = 1; 2; 3)選定以後，其他（tā）的變量可以根據式(4)~式(6) 導出，分別為

1.3 Filippov 係統

振動驅動係統的運動情況（kuàng）不僅取決於內部質量塊的相對振動，而且與其所受的外部阻力有關. 本文中係統所受的阻力為庫倫幹摩（mó）擦，幹摩擦的複雜性在於（yú）其不連（lián）續性，即當（dāng）係統速度方向（xiàng）改變時，摩擦力的變化是階（jiē）躍（yuè）的. 因此（cǐ），就其本質而言，本文所研究的係統，也就是式(2) 和式(8) 所決定的振動驅動係統，是一種右端不連續的微分方程（chéng）係統（tǒng）. 這種不連續的複雜性體現在力學現象上，就是係統會發生粘滑（huá）運動，而這種特殊的運動（dòng）模式又讓傳（chuán）統（tǒng）的分析方法（fǎ）顯得（dé）無能（néng）為力（lì）. 為了更好地從數學上描述（shù）運動方程，以及從力學角度更好地解釋各種運動情形的發生，本文采（cǎi）用Filippov 係統的相關理論分析振動驅動係統. 這樣做的好處是，Filippov 滑移分岔理論能有效地解釋振動驅動係統中的粘滑效應（yīng）. 需要（yào）注意的是，Filippov 係統中所謂的（de）滑移運（yùn）動（dòng），其實就對應了振動驅動係統粘滑運動中的黏滯狀態.

采用Filippov 係統分析的（de）步驟（zhòu）是：建立係統一（yī）階狀態微（wēi）分（fèn）方程；確（què）定滑移區域；具體討論在滑移（yí）區域的邊界（jiè）是否發生滑移分岔. 當然，由（yóu）於本（běn）文（wén）中采用的驅動（dòng）是三相驅動，本身也存（cún）在不連（lián）續現象，所以這又（yòu）增加了分析的複雜性. 基於此，文中（zhōng）通過分類討論，將振動驅動係統中可能（néng）發生的各種滑移分岔現象進行了詳細的羅列、歸納.

具體（tǐ）地，我們首先將(2) 式由二階非自（zì）治係統轉化為（wéi）一階自治係統，即將t 作為狀態變量，引入變量替換，令

式中（zhōng），Hx = 0 是x 的法向量.

分（fèn）界麵上滿足這一條件的區域稱為滑移區域（yù）(sliding region)，記為? Σ. 係統隻有在滑移區域上，才會發生滑移運動，也就是出現黏（nián）滯狀態.根據Utkin 等效控製理論，滑移區域上（shàng）的（de）運（yùn）動由兩個部分構成. 一個是F1 和F2 的平均值，另一個是控製函數β(x)，該函數用來（lái）將流形（xíng）拉回到與滑移區域（yù）? Σ相切，這也（yě）就（jiù）保證了係統的運動（dòng）始終保持在（zài）滑移區域上，具體表達式如下

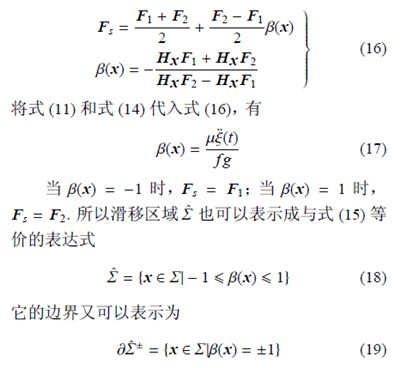
2.運動分（fèn）析

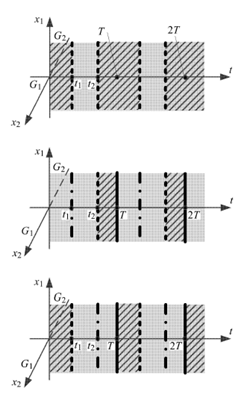
圖3 係統在4 種情形（xíng）(表1) 下的滑移區域示意圖

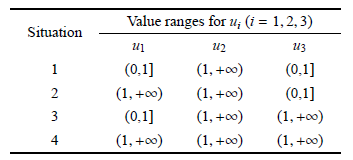
表1 粘滑運動的4 種情形

2.1 情形1

此時，由表1 中的第（dì）一（yī）行數據，等價地得到

注意到x2(t1) = 0，x2(t2) > 0，也就是可（kě）能發生滑移分岔位（wèi）置的速度符號確定，因而（ér）兩點處均不會發生分岔. 此時（shí），係統的運動狀態示意圖對應於圖5(a).

2.2 情（qíng）形2

注（zhù）意（yì）到x2(t2) > 0，x2(T) = 0，也就是分岔位置（zhì）處（chù）速度的符號確定，因而兩點處均不會發生分岔. 係（xì）統的運動狀態唯一（yī），如圖5(b).

2.3 情形3

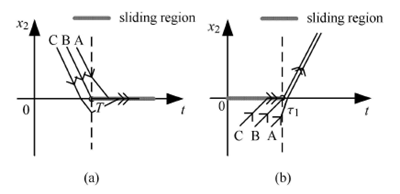
圖（tú）4 係統的（de）兩種分岔示意圖

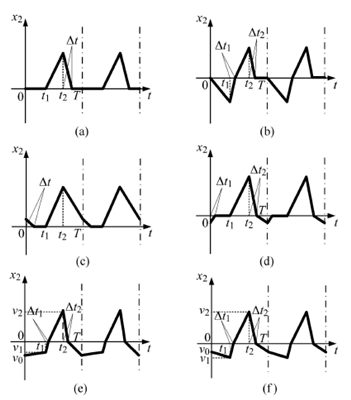
圖5 係統的6 種運動形（xíng）態

3 分岔

第2 節中（zhōng）通過對係統運動分情形進行（háng）分析，觀察到係統運動（dòng）出現了滑移分岔現象，也（yě）得（dé）到了6 種形式的粘滑運動. 但（dàn）是需要注意的是（shì），這並不意味著這6 種（zhǒng）運動形式定性上各（gè）不相同. 本節將先從滑移分岔的觀點分析上述各運動屬於何種滑移運動類型.然後再具體（tǐ）分析各種不同運動發生的條件，探究（jiū）隨著參（cān）數變化它們之間如何（hé）通過滑移分岔實現相（xiàng）互（hù）切（qiē）換.

3.1 歸（guī）納

Filippov 滑（huá）移分岔（chà）理論指出，右端不連續（xù）係統在不連續界麵（miàn）上可能會發生4 種滑移（yí）分（fèn）岔(crossingsliding,grazing-sliding, switching-sliding, addingsliding)[29]，這（zhè）4 種分岔的名稱（chēng）也可以被借用來命名滑移運動的類型. 利用圖3(a)，可以看到在圖5(a)中，係統從（cóng）G1 空（kōng）間進入滑移區（qū）域之後，並不進入G2 空間，而是保持滑移運動直到再次（cì）進（jìn）入G1 空間.可以簡單地理解（jiě）成係統的運（yùn）動狀態（tài）軌（guǐ）跡擦過（guò）滑（huá）移區域，因而這種滑移運動稱為grazing-sliding. 同樣可以看到，圖5(c) 中的滑移運（yùn）動（dòng）也可以看（kàn）成是一種grazing-sliding. 這兩種運動形態可以被歸納為（wéi）同一種滑移運動類型（xíng）.

觀察圖5(b)，並結合圖3(b) 可知，係統（tǒng）由（yóu）G1 空間進（jìn）入滑移區域後保持（chí）滑移運動至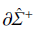

邊界，然後離開（kāi）滑移區域，進入G2 空間. 可以簡單地理解為係統的運動狀態軌跡在經過一段滑移運動之後穿越了滑移區域，因而這種滑移運動（dòng）稱為crossing-sliding.觀（guān）察（chá）圖5(d)，並（bìng）結合（hé）圖3(d) 可知，係統由G1 空間（jiān）直接進入G2 空間，然後又（yòu）回（huí）到滑移區域. 由G2 空間（jiān）進入滑移區域後（hòu），係統滑（huá）移運動至

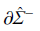邊界，最終回到G1 空間（jiān）. 可以簡（jiǎn）單地理解成，係（xì）統的狀態軌跡（jì）先（xiān）穿過了不（bú）連續界麵（miàn），然後回到滑移區域繼（jì）續運動，對（duì）於這樣一（yī）個（gè）具有來回轉換（huàn）過程的運動，形象地稱（chēng）為switching-sliding.圖5(e) 和圖5(f) 屬於同一類運動，且都不發生（shēng）滑移運動.

圖5(e) 和圖5(f) 屬於同一類運動，且都不發生（shēng）滑移運動.綜上（shàng），係統存在4 種（zhǒng）定性（xìng）不同的運動類型，其中3種運動中存（cún）在黏滯，1種無黏滯發生.

3.2 分岔圖

為了更清晰地描述滑（huá）移分（fèn）岔發生的條件，判（pàn）斷

由第二節的分析，不難發現，如果知道一個係統ui(i = 1; 2; 3) 的取值，以及P1 和P2 的正負（fù）號情況，那（nà）麽係統的運動狀態（tài）可以確定. 從式(26) 和式(27)可以看出，P1 和P2 的正（zhèng）負號情（qíng）況（kuàng）分別與?P1 和?P2 一（yī）致，且最終隻取決於ui(i = 1; 2; 3). 故（gù）而，係統的運動（dòng）狀態從根本上（shàng）講，取決於3 個參數（shù）ui(i = 1; 2; 3) 的取（qǔ）值. 由（yóu）前（qián）文分（fèn）析（xī）可知，隨著這3 個參數變化，係統有（yǒu）如下4 種（zhǒng）類型的粘滑運動.

表2 4種粘滑運（yùn）動的發生條件

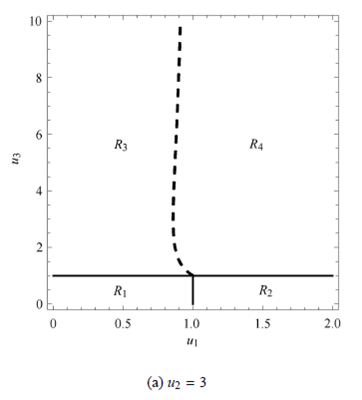
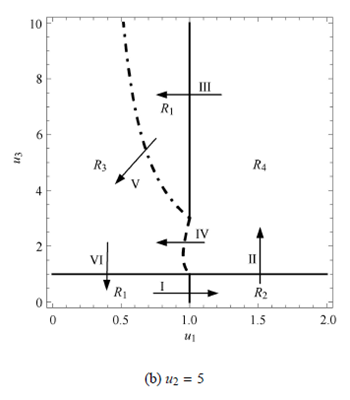
圖6 振動驅動係統在u1--u3 平（píng）麵的（de）分岔圖

Ri (i = 1; 2; 3; 4) 表示發生不（bú）同粘滑（huá）運動的區域，下標i 的值與表2 中的序號對應. 對比圖6(a) 和圖6(b)，發現（xiàn）圖6(a) 中不存在?P1 = 0 這條線，而圖6 (b) 中存在；相應地，圖6 (a) 中的R1 是（shì）1 片區域，而圖6 (b)中的R1 是2 片區域. 由此可知，當u2 的值較小(通過數值（zhí）計算，觀察到大約u2 < 3:5) 時，?P1 < 0 恒成立，看不到所謂的switching-sliding 分岔，而當（dāng）u2 的（de）值較大(大約u2 > 3:5) 時，switching-sliding 分岔可能會發生.

當u2 較大時，運動分類情況較為典型也（yě）較為豐富. 以圖5(b) 為例，從左下角的R1 出發逆時針繞一圈，研究各分岔線或分界線對運動行為的影響. 從R1出發，當u1 的值增（zēng）加時，係統跨過u1 = 1 分（fèn）界線進入R2 (箭頭I)，運動類型由grazing-sliding (圖5(a)) 變成crossing-sliding (圖5(b)). 這是因為隨著u1 增加，係統在第一段時間上的黏滯區域逐步地變為非黏滯區域，無法再保（bǎo）證（zhèng）係統（tǒng）不發生後（hòu）退運動. 從R2 出發，當（dāng）u3 的值增加時（shí），係統跨過u3 = 1 分界（jiè）線進（jìn）入R4 (箭頭II)，運動類型由crossing-sliding (圖5(b)) 變成無黏滯運動(圖（tú）5(f)). 這是因為，隨著（zhe）u3 的增加，僅存的黏滯區（qū）域也逐步變成非黏滯區（qū）域，因而係統將不再黏滯（zhì）. 注（zhù）意到?P1 = 0 與（yǔ）?P2 = 0 兩條曲線（xiàn）在u1 相交，這是因為當u1=1 時，係統在第一（yī）段上加速度為0(見（jiàn）式(2))，所以?P1 = 0 成立（lì），也就意（yì）味著?P2 = 0 成立. 由（yóu）此可知，從R4 出發，係統有兩種選擇（zé），一種是跨（kuà）過u1 = 1 進入R1 (箭頭III)，運動（dòng）類型再（zài）次變成grazingsliding(圖5(c)). 這是因為隨著u1 減小，係統在第一段時間的非黏滯（zhì）區域又變成（chéng）黏滯區域，因而保證係統不會（huì）後退，而且（qiě），這個區域中.P1 > 0，係統在（zài）第三段時（shí）間內會由於慣性保持速度（dù）為正，不會向後運動（dòng）.另外一種（zhǒng），係統（tǒng）從R4 出發，經過.P2 = 0 分岔線進入R3 區域(箭頭IV)，運動類（lèi）型變成switching-sliding (圖5(d))，這是因為跨過虛線，.P2 由負變正，意味著係統在第一段時間上速度由負（fù）值開（kāi）始逐漸增大，且一（yī）定會在t1 時刻之前，達到速度為0. 考慮到第一段時間區間上為滑移區域，因而這會引起（qǐ）switching-sliding運動. 從（cóng）R1 出發，跨過.P1 = 0 分岔線，係統也會進入R3(箭頭V)，這是因為點劃線左邊.P1 < 0，意味著x2(0) < 0，而第一段時間（jiān）區間為滑移（yí）區域，因而會發生switching-sliding 運（yùn）動. 最後，從（cóng）R3 出發（fā），隨著u3減小，係統會回（huí）到R1 區域(箭頭VI). 這是因為，係（xì）統（tǒng）在第三段時間上的非粘滑區（qū）域變成了粘滑區域，再次保證了（le）係統不會向後運動.

4.數值（zhí）驗證

由第3 節（jiē）可知，決定係統分岔特性的變量（liàng）是驅動參數ui(i = 1; 2; 3)，為了驗（yàn）證（zhèng）分岔結果是否正確，以及運動特性是否與理論分析一（yī）致，有必要對其進行數值計算的驗證. 本節中物理參數固定，唯一改變的是驅動參數. 這（zhè）裏選（xuǎn）定L = 1 m, u = 0:333 3,g = 10m/s2, f = 0:2，通過改變控製驅動參數wi(i = 1; 2; 3)，可以得（dé）到（dào）所有類（lèi）型的運動特性圖形. 本節中取u2 = 5，這樣係（xì）統（tǒng）的粘滑運動類型可（kě）以由圖（tú）6(b) 直觀地看出. 圖7 通過數值計算，得到了係統在不同區域的速度時間圖. 通過（guò）比較表3 和圖7，發現（xiàn）理論分析出（chū）的運動類型和數值（zhí）計算（suàn）的運動形態吻合.通過對比圖（tú）5 和圖7，發現運動形（xíng）態的理（lǐ）論分（fèn）析（xī）和數值計算結果吻合. 由此，驗證了本文中理論分析的正確性.

表3 數值計算四組驅動參數

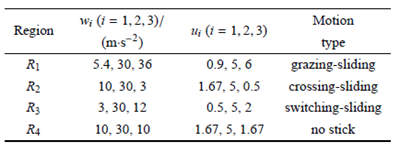
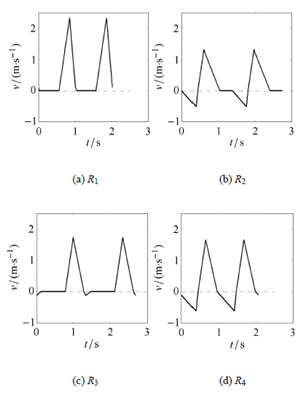
圖（tú）7 數值方（fāng）法（fǎ）得到的係統在不同區（qū）域的速度時程圖

5.結論

本文研究（jiū）了受三相驅（qū）動的振動（dòng）驅動係統在水平麵上的直線運動. 不同（tóng）於以往的研（yán）究，本文重點關注（zhù）了係（xì）統在各（gè）向同性幹摩（mó）擦下的運動. 這種環境與（yǔ）物理實際比較吻合（hé），研究工作具有潛在的實用價值（zhí）.含庫倫幹摩（mó）擦的振動驅動（dòng）係統是一種Filippov係統，因而本文采用滑移分岔的（de）理論分析了其粘滑運動. 在隻考慮係統（tǒng）向前運動的情況下，可以將運動分成4 種基本情（qíng）形. 對4 種情形分類討論，並加以歸納（nà），最終（zhōng）得到4 種不同的粘滑運動. 借助理論分析得到的分岔條件，我們給出了在（zài）驅動參數（shù）wi (i = 1; 2; 3)變化時，係統運動的分岔圖. 通過數值（zhí）模擬（nǐ），運動（dòng）分類以（yǐ）及各種運動形態的正確性都得到了驗證.通（tōng）過本文的滑移分岔分析，可以看到，三相（xiàng）振動（dòng）驅動係統在各向同性幹摩擦環境下具有豐富的動力（lì）學行為（wéi），值得進一步的實驗（yàn）驗證和（hé）探究. 此外，從結構上改善和提升振動驅動係統，使（shǐ）其更好地適應各向同性（xìng）幹摩擦環境（jìng），也（yě）是未來值得思考的問題（tí）.

綜上，係統存在4 種定性不同的運動類型，其中3種運動中存在黏滯（zhì），1種無黏滯發生（shēng）.

投稿箱：
如果您有機床行業、企業相關新聞稿件發表，或進行（háng）資訊合作（zuò），歡迎聯係（xì）本網編輯部，郵箱：skjcsc@vip.sina.com

更多相關信（xìn）息

名企推薦

業界視點

| 更多

行業數（shù）據

| 更多

博（bó）文選萃

| 更多

數（shù）控機床