基於量子粒子群優化算法的機器人運動學（xué）標定（dìng）方法-機（jī）器人-數控機床市場（chǎng）網

您現在的位置：機器人> 技術前沿>基於量子粒子群優化算法的機器人運動（dòng）學標定方法

基於量（liàng）子粒（lì）子群優化（huà）算（suàn）法的機器（qì）人運動學標定方法

2017-1-5 來源（yuán）：東北大（dà）學機械工程（chéng）與自動化學（xué）院作者：房立金黨鵬飛

摘要：基於量子粒子群優化算法，提出一（yī）種同樣適用於串聯（lián）機器人和並聯機器人（rén）的運動學標定方法。利用閉環矢量鏈方法和Denavit．Hartenberg矩（jǔ）陣法，分別建立並聯機器人（rén）和串聯機器人的運（yùn）動學誤差模型，將運動學誤差模型內的幾何誤差源作為相應的機構參數修正量。由於機器人運動學誤差模型表（biǎo）現有較強的（de）非線性，因此確定（dìng）模型內的機構參數修正量為優化變量（liàng），將（jiāng）機器人運動學參數標定問題轉化為非線（xiàn）性係統的優化問題。采用量子粒子（zǐ）群優化算法對優化問題（tí）進行求解，利（lì）用優化獲得的參（cān）數修正量更新運（yùn）動學模型，以達到提高機器人運動精度的目的。以五軸並聯機床的平麵約束（shù）機構為研究對（duì）象，通過試驗驗證該標定方法的標定效果，並與模糊插值標定方（fāng）法進行比較分析，結（jié）果表明在較大的工作空間內基於量子粒子群優化的運（yùn）動學標定方法更為有效。

關鍵詞：機器人；位姿誤差；運動（dòng）學標定；量子粒子群優化（huà）

0.前言

不論是串聯（lián）機器人還是並聯（lián）機器人，在現有（yǒu）條件下還無法對機器人的末端（duān）位姿進行實時和直（zhí）接的測量。現有的（de）一般方法是利用機器人的機（jī）構關（guān）節參數和運（yùn）動學模（mó）型通過計算來間接地獲得。因此機器人的末端位姿精度在很大程度上取決於機器（qì）人的關節（jiē）參數的標定精度。機器人由於結構特征、安裝位姿等因素的影響，現場直接測量所得到的機構參數往往不夠（gòu）準確，直接導致了機器人末端位姿精度的（de）降低（dī）。因此，機器人機構參數的獲取即機器人的（de）運動學標定問題是機器人高（gāo）精度定位（wèi）控製的基礎和核心（xīn）問題，同時也是機（jī）器人領（lǐng）域的難點問題（tí）之（zhī）一。機器人的運動（dòng）學標定～直（zhí）是（shì）機器人學研究領域的（de）一項重要內容，國內外學者針對標定問題做了（le）大量研究工（gōng）作。SUN等u1提出了一種新的基於閉（bì）環矢量法的誤差源分類方法，將幾何誤差（chà）源分為補償誤差（chà）和非補償誤差（chà）兩種，為誤差的標定（dìng）、補償提供了幫助。VERL等根據辨識矩陣條件數確定了測量構型的（de）選（xuǎn）取方法，研究了測量構型的選取數量（liàng）與末端位姿誤（wù）差之間的關係。為了提（tí）高了標定效率，REN等p1提出通過安裝雙軸傾角儀來調節運動平台的姿態，在（zài）姿態約束的情況下選（xuǎn）取有效測量構（gòu）型進行運動學標定，並利用仿真和試驗驗證（zhèng）了這（zhè）種方法的有效性。BAI等【41則（zé）提出一（yī）種模糊差值標定方法，不僅簡化了標定過程，而且適合並聯機器人工作空間較小的特點。ZHANG等15-6]提出一（yī）種並聯機器人誤（wù）差綜合補償方法，基（jī）於虛擬誤差理論將幾何誤差、熱誤差等假設成單一的虛擬誤差源，利用共存演化神經網絡算（suàn）法對虛擬誤差實現了補償。

近年來，粒子群（qún）優化算法(Particle swarmoptimization，PSO)已經被逐步地應用於（yú）機器人運動精度、路徑規劃等領域的相關研究（jiū）中。特別（bié）是量（liàng）子粒子群優化算法（fǎ）(Quantum—behaved particle swarmoptimization，QPSO)，以量子物理基（jī）本理論為基，與粒子群優化算法相比具有更好的全局搜（sōu）索能力，更適合機器人（rén）學研究中的多參數組合（hé）優化問題（tí）。黃進等（děng）p1利用PSO算法（fǎ）對外部軸內關（guān）鍵參（cān）數進行優化，試驗表明機器人與（yǔ）外部軸係統的整體精度有了較大的提高。謝平等ll叫利用PSO算法對並聯（lián）機器人驅動杆杆長參（cān）數進行優化，有效地修正了期望軌跡與理想軌跡之間的偏差。LI等【lu將神經網（wǎng）絡與PSO算法相結合，對並聯機器人的運動學正解進行求解，仿真結果顯示該方法能夠達（dá）到並聯機器人在線控製所需的運算速度與求解精度（dù）。JUANG等llzJ基於（yú）PSO算法與遞歸神經網絡兩種算法提出（chū）一種新的機器人動力學步態學習方法，並在（zài）一（yī）款hexapod型機器人的（de）步態控製器（qì）上成功使用。COUCEIR等u糾將PSO算法應用於多機器人係統的研究中，在仿真與試驗環境下實（shí）現（xiàn）了多機（jī）器人的避障功能（néng）。史（shǐ）也掣141提出了一種基（jī）於QPSO算法的路徑規劃方法，通過規劃空間機器人機械（xiè）臂關節角的運動，使得基（jī）座姿態（tài）和（hé）機械臂末端姿態能夠同時到達（dá）期望狀（zhuàng）態。

本文在上（shàng）述（shù）研究的基礎上，提出一種同樣適用於串聯、並聯機器人的運動學標定方（fāng）法。首先，對典型的串聯（lián）機器人、並聯機器人分別進行（háng）運動學分析，建立包含鉸鏈中心位置誤差（chà）、轉動軸線偏轉誤（wù）差、杆件長（zhǎng）度（dù）誤（wù）差（chà）等誤差源的（de）誤差模型，將模型內的誤差源作為相應的機構參數修正量。然後，將（jiāng）機器人的運動（dòng）學標（biāo）定問題轉化為非線性係統的優化（huà）問題，以機構參（cān）數的修正量作為優化（huà）變（biàn）量，以機器人位姿（zī）精（jīng）度要求設計目標函數，基於位姿誤差模型建立一個多參數的非線性優化係統。最後，利用量子（zǐ）粒子群（qún）優化算法對（duì）目（mù）標函數進行計算（suàn），根據獲得的機構（gòu）參數修正量更新運動學模型，實現對機器人機構參數的標定。

需要（yào）指出的是，影（yǐng）響機構參數的誤差因（yīn）素有很多，包括隨機誤差和係統誤差（chà）等。本文方法隻是針（zhēn）對關節誤差中的係統誤差進行求（qiú）解標定，不適用於間（jiān）隙等典型的隨機誤差。

1.機器人機構參數標（biāo）定流程

並聯機（jī）器人和串聯機器人的運動學（xué）求解具有不同的特點，本文利用並聯機器人的逆運動學方程（chéng）和串聯機器人的正運動學方程來建立相應的（de）標定模（mó）型。

並（bìng）聯機器（qì）人的標定流程如圖1所示：①利用逆運動學方程建立機器人的位姿誤差模型；②根據測量和標定的需求選擇適當的構型及相應的理想位姿上L；③利（lì）用逆運動學方程計算理想情況下對應的機構參數知：④基（jī）於實際測（cè）量得到的末端位姿誤差e，利用量子粒子群算法進（jìn）行尋優，計算機構參數修正量卻；⑤將（jiāng）機構（gòu）參數修正量卻與理想機構參數g。相加得到最優機（jī）構參數g，作為並聯機器人運動學標定的（de）結果。

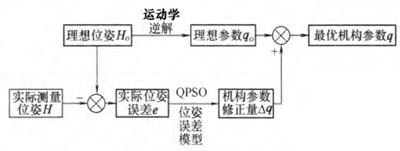
圖（tú）l並聯機器人標定流程

串聯機器人的標定流（liú）程如圖2所示：①利用（yòng）正運動學方程建立機器人的位姿誤（wù）差模（mó）型；②根據測（cè）量和標定的需（xū）求選（xuǎn）擇（zé）合適的理想機構（gòu）參數劬；③利用正運動學模型（xíng）計算理想情（qíng）況下對應的末端位姿玩；④根據實際測量得到的末端位姿誤差e，利用量子粒子（zǐ）群算法（fǎ）進行尋優，得到機構（gòu）參數修正量幻；⑤將機構參數修正量卻與理想機構參數銣相加得到最優機構參數g，作為串聯（lián）機器人運動學標定的結果。

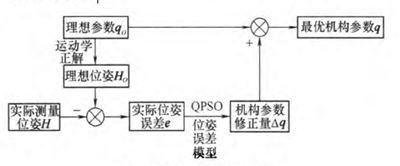
圖2串聯機器人標定（dìng）流程

2.量子粒子（zǐ）群優化算法的基本原理

量子粒子（zǐ）群優化（huà）算（suàn）法，由Ⅳ個代表潛在問（wèn）題解的粒子組成群體，在一個M維的目標搜索空間內進行搜索。在t時（shí）刻，第（dì）f個（gè）粒子的位置為

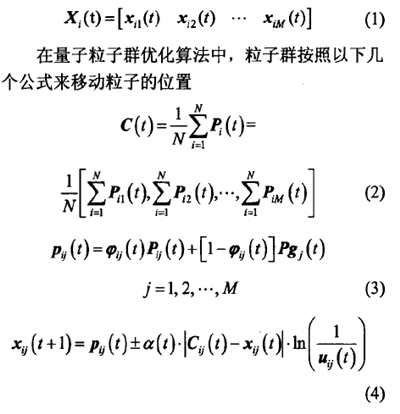
3.機器人位姿誤差（chà）建模

分別選用比較典型的Stewart並聯機器人（rén）、Puma560串聯關節型機器人作為機器人運動學模型的建模對象，建立機器人內主要誤差源與末端位姿誤差之間的關係。

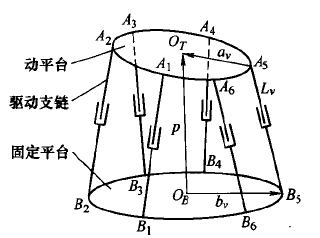
3．1並（bìng）聯機器人位姿誤差模型（xíng）

3．2 串聯（lián）機器人位姿誤差模（mó）型

圖4 Puma560串聯（lián）機器人結構簡圖

4.基於量子粒子（zǐ）群（qún）優化算法的標定問題求解

將標定問題轉（zhuǎn）化為非線性係統的最優化問題，利用量子粒子群優化算法進行求解。

4．1確定優化變量

確定機構參數修正（zhèng）量△g為最優化問題求解的目標變量。由運動學方程式(8)與式(10)可以看出，通（tōng）過調整機器人誤差模型中的各類（lèi）誤差源可以影響（xiǎng）機器人的末端位姿。將模型（xíng）內誤差源作為（wéi）相應的機構參數修正量卻，利用（yòng）優化算法尋（xún）找一組最優的修正量衄就可以實現機器人（rén）機（jī）構參數（shù）的標定（dìng）。另外，由（yóu）於本文研究重點在於機器人機構參數（shù）的標定，所以對驅動杆的控製誤差（chà）不（bú）予考（kǎo）慮。因此（cǐ），將機構參（cān）數（shù）修正量幻確定為（wéi）最優化問（wèn）題（tí）的優化變量。對於求解最優化問題的量子粒子群優化（huà）算法，每個粒子都代表一組用於優化機器人機構參數的解，其位置（zhì）矢量X(幻就是最優化問題（tí）的優化變量，即機（jī）構參數修正量（liàng）卻。

4．3量子粒子群優化算法的計算步驟

設（shè）粒子（zǐ）數為Ⅳ，迭代次數用t表示，最大迭（dié）代次數為（wéi）‰。。利用量（liàng）子粒子群優化（huà）算法計算標定問題的具體（tǐ）流程如下。

(1)在機器人工作空間內選取肛組構（gòu）型進行測量，得到相應的實際測量位姿日，通過計算得到實際位姿誤差eh，h=1，2，...,μ。

(2)初始化粒子群算法相關（guān）參數。置t=O，根據式(1)，隨機（jī）初始化Ⅳ個粒子的初始位置X(0)，粒子位（wèi）置矢量的維數M等於相應類型機器人機構參數（shù）修正量△口的維（wéi）數。

(5)根據量子粒子群優（yōu）化算法，利用式(2)～(4)分別計算粒子群的平均最優（yōu）位置aD以及每個粒子的隨機點位置p，，更（gèng）新每（měi）個粒子的位（wèi）置矢量Xi(T+1)。

(6)判斷是否滿足迭代算法的終止條件，即機器（qì）人運動精（jīng）度要求。如果滿足，粒子群的全局最（zuì）優位置Pg(t)就是機器人運動學標（biāo）定問題的最優解△q，將（jiāng）其與理想機構（gòu）參數q0。相加（jiā）就能得到標定後的最優機構參數q；若（ruò）未滿足終止（zhǐ）條件，返回步驟(3)繼續計算。另外，當t=tmax，計算結（jié）束。

5.五軸並聯機床試驗分（fèn）析

5．1五軸並聯機床結構簡介

五軸並聯機床結構圖如圖5所示，該機構由固定平（píng）台、工作平台、動平台、平麵約束機構、四個驅動分支構成。五軸並聯機床采用高剛度且力流封（fēng）閉的龍門結構。固定（dìng）在兩側立柱頂端的四個伺服（fú）電動機分別驅（qū）動（dòng）四組滾珠絲杠副，滾珠（zhū）螺母(滑（huá）塊)通過四根支杆與（yǔ）動平台相連，通（tōng）過調整滑塊（kuài）的位移來實現動平台的運動。在固定平台、動平台之間j由四塊板件組成了平麵約束機構，約束機構部分內各轉動（dòng）軸線與工作台（tái）運動方向平行。

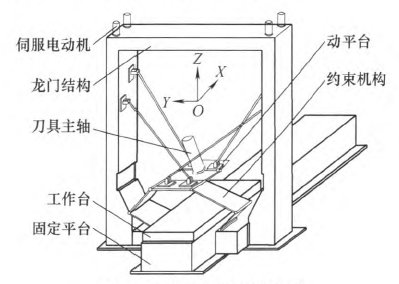
圖（tú）5五軸並聯機床結構圖

5．2約（yuē）束機構部（bù）分誤差模型（xíng）

根據約（yuē）束機構部分（fèn）的結構特（tè）征及其平（píng）麵運動的特性，將平麵約束機構（gòu）、動平台以及工作台綜合簡化為六杆（gǎn）串聯機構(圖6)。如果各轉動副軸線問的平行度（dù）誤差較大，嚴重時甚至會影（yǐng）響（xiǎng）到約束機構部（bù）分運動自由度的數量，所以機構內安裝（zhuāng）的轉動副具有較高的精度水平。假設（shè）鉸鏈間隙以及軸線間的平行度誤差較小，可以忽略（luè）。因此，平麵約束機構內的幾（jǐ）何誤差（chà）源主要包括工作台姿態誤（wù）差以（yǐ）及各杆（gǎn）件的長度誤差。

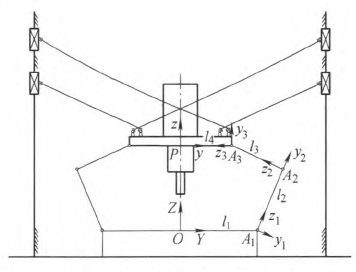
圖6 五軸並聯機床原理簡圖

經過上述分（fèn）析，將約束機構部分內主要誤（wù）差源轉化為機構參數修正量（liàng）卻，經整理如表（biǎo）1所示。其中，工作（zuò）台的姿態誤差（chà）被分為（wéi）繞Y軸（zhóu）與繞Z軸的偏轉修（xiū）正量。

表1約束機構部分（fèn）機構參數修正量

然後（hòu），根據約束機構部分結（jié）構參數的設計值，依次（cì）沿轉動副Al、A2、A3，建立由基坐標係D係到（dào）動坐標係JP係的理想位姿方程

這樣即可得到約束機構部（bù）分的運動學模型，建立起（qǐ）各項機構參數修正量與末端位姿誤差之間的聯係。

5．3基於量子粒子（zǐ）群優化算法的（de）標定試驗

通過（guò）調整模型內各參數修正量可以（yǐ）對動（dòng）平台各個方向上（shàng）的位置誤差產生影響，而作為機（jī）床驅動部分的並聯機構部分能夠對（duì）其中y軸、z軸方向上的位（wèi）置誤差進行補償。因此（cǐ），在針對五軸並聯機床約束機構（gòu）部（bù）分進行的（de）運動（dòng）學標定試驗中，利用（yòng）工作台運動Ⅸ軸)方向上的精度要求建立優化目標函數，對約束機構（gòu）部分的機構參數進行標定。

表2 x軸向末端位置誤（wù）差測量結果

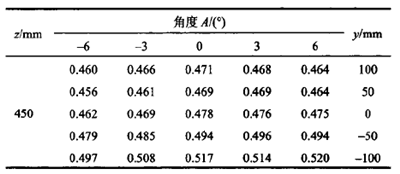
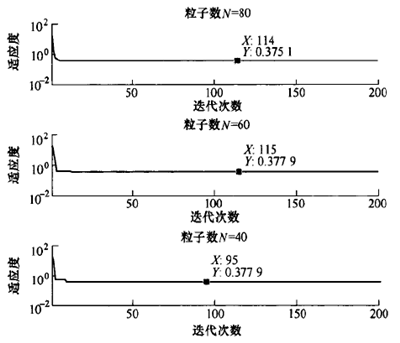
圖7迭代計算結果

結果表明，粒子數對於QPSO算法的收斂效（xiào）果（guǒ）影響較小（xiǎo），當粒子數由60增加到80時，最小適應度從0．377 9減小到0．375 1，標定效果的提高程度較小，但（dàn）同時降低了效（xiào）率。當粒子數為40時，僅用95次迭（dié）代就獲得了（le）相同的最（zuì）小適應度0．377 9，表（biǎo）明了QPSO算法具有一定的隨機性。取粒子數N--60的迭代計算結果，獲得機構參數修正量的優化結果，如表3所（suǒ）示。

表3機構參數修正量

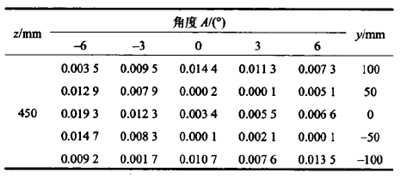
將修正量引入（rù）約束機構部分的運動學模型，得到優（yōu）化後的x軸向末（mò）端位置誤（wù）差(表4)。結（jié）果中顯示優化後最大（dà）誤差為0．019 3 mill，最（zuì）小誤差為0．0001 mlil，平均誤（wù）差約為0．007 5 mill，經過參數優化後，X軸向的位置精（jīng）度有了明顯改（gǎi）善（shàn）。

表4優化後的X軸（zhóu）向末端位置誤差

利用模（mó）糊差值標定方法對（duì）Stewart並聯機器人進行（háng）了運動學標定，標定後在（zài）10 rrlrnx 10lain×10 IIllll的立方體空間內，最大位置誤差為0．049 5 rain，平均誤差為0．001 1 min；在（zài）20mmx20minx20 mill的空間內，最大位置誤差為0．091 2 mm，平均誤差為（wéi）0．010 8 mnl。與模糊差值標定結果相比，基於量子粒子群優化算法的（de）標定方法能夠在更大的工作空（kōng）間（jiān）內實現運動（dòng）學參數（shù）的（de）有效標定（dìng）；而且最（zuì）大末（mò）端位置誤差為0．019 3 rain，標定效果的均勻性更好。

6.結論

(1)針對並（bìng）聯、串（chuàn）聯兩類機器人進行誤差建模，分析標定流程，基於量（liàng）子粒子群優化算法，提出了一種適用於並聯機器人與串聯（lián）機器人的標（biāo）定方法，能夠實現機器人關節變量和（hé）其他（tā）關節（jiē）參數的有效辨識。

(2)機器人關節結構較為複雜（zá），完成裝配後對機構關節參數直接進行測（cè）量標定的難（nán）度較大（dà）。利用量（liàng）子（zǐ）粒子群優（yōu）化（huà）算法（fǎ）具有全局優（yōu）化能力的特點，對非線性（xìng）運動學模型中的機構（gòu）參數進行優化，可以將複（fù）雜的運動學標定問題簡單化。

(3)以五軸並聯機床的約束機構部分為例，利用實測數（shù）據獲得的標定（dìng）結果（guǒ）表明了基（jī）於量子粒（lì）子群優化算法的（de）標定（dìng）方法是一種快（kuài）速的、能夠有效改（gǎi）善精度（dù）的標定方法。

投稿箱：
如果您有機床行業、企業相關新聞稿（gǎo）件發表，或進行資訊合作（zuò），歡迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視（shì）點

| 更多

行業數（shù）據

| 更多

博文選萃

| 更多

數控機床（chuáng）