精密（mì）研拋數控機床（chuáng）幾何誤（wù）差與熱誤差複合建模（mó）及其補償研（yán）究（jiū）-機床電器網-數（shù）控機床市（shì）場網

您現在的位置：機床電器網> 技（jì）術前沿>精密研拋數控機床幾何誤差與熱誤差複合建模及其補償研究

精密研拋（pāo）數控機床（chuáng）幾何誤差與熱誤差複合建模及其補償研（yán）究

2016-11-10 來源（yuán）：長春工業大學作者：張恩忠,李剛,林潔瓊,冉同歡（huān）

摘要:為了（le）提（tí）高精（jīng）密研拋數控機（jī）床的加工精度,對研拋（pāo）數控機床的幾何誤差與熱誤差進行了研究與分析（xī）,發現隨著機床相關部（bù）件溫度的不斷升高直至熱穩態,機床的（de）定位（wèi）誤差也不斷（duàn）增加到穩態值,驗證了（le）幾何誤差和熱誤差是精密及（jí）超精密加工誤（wù）差的主要來源。綜（zōng）合考慮了（le）機床複合誤差的不同特點（diǎn）並進（jìn）行誤差分離,提出（chū）了基於牛頓（dùn）插值算法和最小二乘法的幾何與熱複合誤差建模方法,依據複合誤（wù）差模（mó）型（xíng）進（jìn）行補償（cháng）實驗, 補償後機床（chuáng）冷態下定位誤差值從3. 5μm 降至（zhì）1. 2μm, 誤差降低了65． 7%,熱穩態後定位誤差值從（cóng）12. 2μm 降至1. 9μm,誤差降低了84. 4%,實驗結果證明複合誤差模型計算簡單、預測精（jīng）度高、具有較好的魯棒性,為提高機床的（de）加（jiā）工精度提供了理論與實（shí）踐依據。

關（guān）鍵（jiàn）詞:研拋數控機床;插值算（suàn）法;複合（hé）誤差模型;誤差（chà）補償

0.引言

由機（jī）床本身（shēn）製造、裝配精度引起的幾（jǐ）何誤差和由機床在加工過程中熱變形引（yǐn）起的熱誤（wù）差是影響數控（kòng）加工精度的關鍵因素。在精密、超精密加工中（zhōng）,數控（kòng）機（jī）床的幾何（hé）誤差和熱誤差約占（zhàn）總誤（wù）差的70% [1-2] ,其中（zhōng）熱誤差是影響機床加工精度的主要因素。數控機床熱誤差形成的原因多種多樣,其（qí）中包括機床所處的加工環境、機（jī）床上各種熱源影響、人為造（zào）成的因素等,國內外學者對數控誤差建模和補（bǔ）償方法進行了廣（guǎng）泛研究,文獻[3]趙幗娟等建立了四軸拋光平台的綜合誤差模型並（bìng）分析其誤差的主要來源、文獻[4]韓飛飛等對數控機床的幾何精度進行（háng）了綜合分析,並驗證了定位誤（wù）差是影響機床幾何誤差（chà）最主要的因素、文獻[5]重點研究了機床表麵的輪廓誤差與幾何誤差之間的耦合關係並進一步分析（xī）與研究了機床導軌的精度,雖然上述都考慮了幾（jǐ）何誤差的影響,但都忽略了熱引起的誤差因素。相關學者對熱誤差建模方法做了大量的研（yán）究,其中包括（kuò）基於支持最小二乘（chéng）向量（liàng）機[6] 、模糊（hú）神經網絡[7] 、灰色理論[8] 、回歸分析[9] 等,雖然這些誤差建模方法的預測精度較高,但在實（shí）踐操作過程中（zhōng）還（hái）存在（zài）建模方法較複雜且時間（jiān）較長,模型魯（lǔ）棒性較低（dī）等一些缺點。

本文在一台（tái）自主搭建的精密研拋數（shù）控機床上進行試驗與研究,綜合考慮了不同溫（wēn）度狀態下機床定位誤差的變化規律與相互關（guān）係,根據幾何誤差與熱誤差的不（bú）同特點進行誤差分離,基於牛（niú）頓插值算法和最小（xiǎo）二乘法對機床分別建模,再綜合可得到幾何與（yǔ）熱的複合誤差數學模型,通過補償實（shí）驗驗證了該模型計算簡便,擬合精度高,易於程序設計,為提高機床的加工精度提（tí）供了理論依據（jù）。

1.研拋機床複（fù）合元素建模原理與測量

1. 1　複合（hé）誤差建模原理

複合誤差（chà）是指與機床溫度和（hé）位置坐標都相（xiàng）關的誤差元（yuán）素。複合誤差建模過程（chéng）比較複雜,先要進行幾何誤差與熱誤（wù）差的分離(如圖1 所示),然後（hòu）再對幾何（hé）誤差和熱誤差分別建模。采用位置K 的（de）多項式擬合得到機床冷態下的幾何誤差模型,機（jī）床不同時間的熱誤差元素（sù）與機床溫度相關,對不同（tóng）時間的各（gè）熱（rè）誤差曲線進行一次擬合得到相應斜率,依據各時間段（duàn）的溫度、斜率值構造熱誤差模型,最後將以上兩種誤差模型合成（chéng）為一個複合（hé）誤差模（mó）型。

圖1　複合誤差分離圖

與機（jī）床溫度和位置坐標都有關的複合誤差元素可表達為:

1. 2　複合誤差元素測量

為了測量機床（chuáng）y 軸不同時刻的定位誤差和溫度變（biàn）化值,如圖（tú）2 所示（shì）,選用鉑（bó）電阻式Pt100 溫（wēn）度（dù）傳感器和16 通道的XSR90 彩色無紙記入儀進行溫（wēn）度測量（liàng）,根據相關性分析[11] ,溫度傳（chuán）感器T1、T2、T3、T4 分別放在機床的（de）y 軸平台上,T1、T2 用來測量y 軸動導軌和直線電機動子的（de）溫度,T3、T4 用來測量y 軸定導軌和直線電機定子的溫度,首先（xiān）記（jì）入（rù）機床冷態時y 軸各測量部件（jiàn）的（de）溫度值,然後每隔20、40、6090、120、及150min 記入其溫度變化值。

圖2　溫度與誤差測量現場

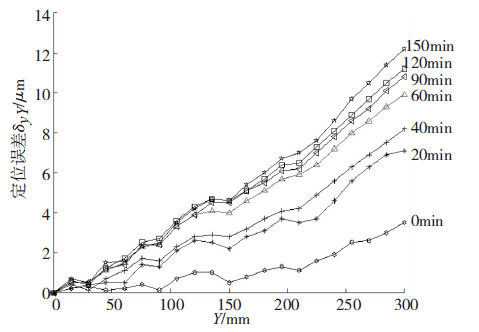
圖3　不（bú）同時段的定位誤差

圖3 為機床不（bú）同時（shí）刻的七條定位誤差曲線,從圖3 中可以看出,機床（chuáng）y 軸的定位誤差隨著機床溫度上升而增大,圖中七條定（dìng）位誤差曲線（xiàn）形狀的變化規律基（jī）本一致,隻是各條（tiáo）曲線的斜率隨機床y 軸溫度（dù）的升高而不斷（duàn）變大,即機床在不同溫度下的定位誤（wù）差可以看成是機床冷態下定位誤差繞機床坐標原點旋轉一定角度而來,這一規律為式(1)複（fù）合誤差建模提供了理論依據。

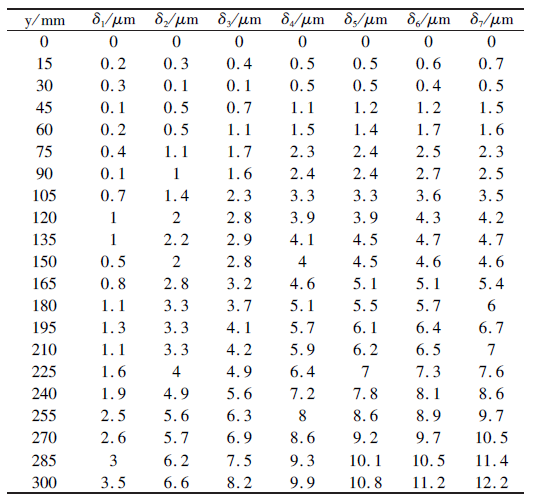
表1 所列δ1 、δ2 、δ3 、δ4 、δ5 、δ6 、δ7 為機（jī）床從冷態時（shí）至達到熱穩態時7 個階段的定位誤差值,由表1 和圖3中看出前3 個時間段機床誤差上升較快,常溫下機床的最大（dà）定位誤差（chà）值（zhí）與達到熱平衡狀態的（de）最大定位誤差（chà）值相差大（dà）約為9μm,這說明研拋數控機床定位誤差受熱影響較大。

表1　定位誤差測量值

2.研拋機床複合元素建模

2. 1　幾何（hé）誤差建模

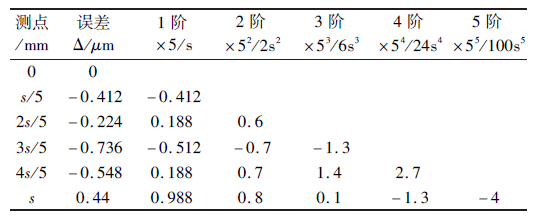
由複合（hé）誤差建模原理分析可（kě）知,熱引起的誤差與誤差曲線的斜率和機床坐標（biāo）位置有關,所以（yǐ）幾何誤差和熱（rè）誤差建模的時候首先將機床（chuáng）冷（lěng）態時的（de）誤差曲（qǔ）線旋轉為水平位置(如圖4 所示),然後對旋轉後的誤差進行（háng）幾何建模,本文對旋轉後的誤差采用牛頓插值法進行（háng）幾何誤差建模,運用激光幹涉儀測（cè）量研拋機床定位誤差,y 軸行程為s = 300mm,測量（liàng）間隔為15mm,每次測得21 個測量點,應用牛頓插（chā）值法,每隔4 個測量點選（xuǎn）取定位誤差,選取冷態下(0min)6 個(機床（chuáng）原點誤差為0)誤差值Δ(旋（xuán）轉後)與坐標位置構造5 階均（jun1）差,均差表如表2 所示。

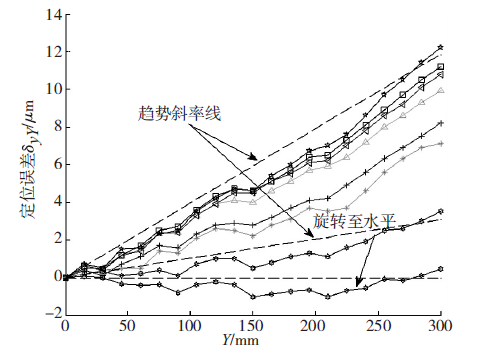
圖4　Y 軸誤（wù）差（chà）旋（xuán）轉

表2　均（jun1）差表（biǎo）

2. 2　熱誤差建模

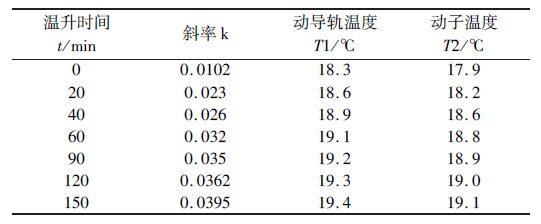
對圖4 所示的7 條誤差曲線進行一（yī）次擬合,可以得到不同溫度下的趨（qū）勢線斜率。根據相關（guān）性分析,機床y 軸（zhóu）電機動子和動導軌溫（wēn）度對y 軸誤差（chà）影（yǐng）響比較大,所以選取這兩個測溫點進行y 軸熱誤差建模。機床不同（tóng）時間下的溫度測量值與各條誤差曲線的趨勢線（xiàn）斜率值的對應關（guān）係如表3 所示。

表（biǎo）3　溫度與斜率統計表

將旋轉後的幾何誤差模型式(3)以及熱誤差趨（qū）勢線模型式(6)代入到式(1)可得y 向幾何誤差與熱（rè）誤（wù）差的複（fù）合模型為:

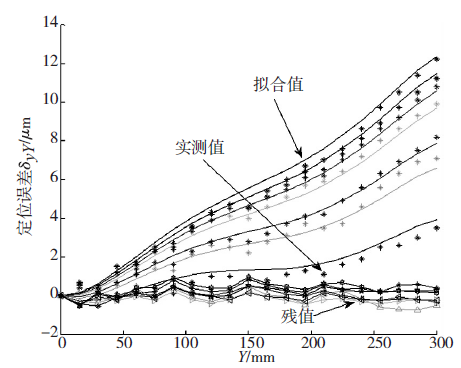
圖5　Y 軸誤差擬合

3.誤差補償實驗

提高機床精度的方法有兩種[10] ,分別為誤差補償法和誤差防止法,誤差防止法是（shì）試圖通過提（tí）高（gāo）機床本身（shēn）的（de）設計、製造和裝配（pèi）等精度來盡可能的減少（shǎo）誤差來源（yuán）,誤差補償法是人（rén）為地造（zào）出一種新的補償去抵消（xiāo）機床原始的誤差,誤差補償法（fǎ）相比誤差防止法費用低（dī）、效率高,是提高數控機床加（jiā）工精度的（de）主要手段（duàn）。

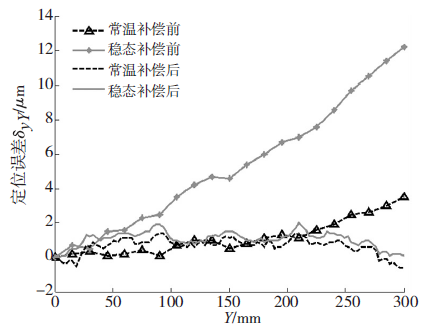
圖6　Y 軸（zhóu）誤差補償效果

本次試（shì）驗采用（yòng）誤差（chà）補償法, 借助精密（mì）研拋數（shù）控機床誤差補償控製器模塊, 依據式(7) 幾何誤差（chà）與熱誤差複合模型計算得到的機床冷態和（hé）穩態時（shí）的補償量輸入到機（jī）床誤差補償表中進（jìn）行補償實驗（yàn）,補償結果如圖6 所示,冷態（tài）時（shí）最大定（dìng）位誤差從3. 5μm 降低到1. 2μm,誤差降（jiàng）低了65.7%,穩態時最大定位誤差（chà）從（cóng）12. 2μm 降到1. 9μm, 誤差降低了84.4%,補償效果十分顯著（zhe）。

4.結論

(1)本（běn）文依據精（jīng）密研拋數控機床y 軸（zhóu）溫升與其定位誤差變（biàn）化關係的基礎上,提出了基於牛頓插值（zhí）法與最小二乘法（fǎ）的幾何與熱複合誤差（chà）建模方法,該誤差模型計算量小,效率高,可以獲得較高的預測精度。

(2)根（gēn）據幾何誤差與熱誤差（chà）的複（fù）合模型對機床（chuáng）進行誤差（chà）補償實驗,實驗表明該模型可以在不同溫度和工況條件下進行誤差補償,補償效果顯著,有（yǒu）效提高了機床的加工（gōng）精（jīng）度。

投稿箱：
如果您有機床（chuáng）行業、企業相關新聞稿件發表，或進行資訊合（hé）作（zuò），歡迎聯係本網編輯部，郵箱（xiāng）：skjcsc@vip.sina.com

更多相關信息

名企推薦

業界視點

| 更（gèng）多

行（háng）業數據

| 更多

博文選（xuǎn）萃

| 更多