複雜曲麵五軸數控無幹涉(shè)刀軸規劃
2020-12-29 來源:南京工業大學機械與動力工程學院 作者:濮瀟楠,劉旭,淩祥
摘 要:五軸數控被廣泛應用於複雜曲麵零件的加工製造,豐富的刀(dāo)軸姿態(tài)是五軸數控的優勢,但幹涉避(bì)讓是刀軸規劃的難點。將複雜曲麵零件離散為點雲模型(xíng),在任一刀觸點處建立初(chū)始(shǐ)刀軸空間,計算初(chū)始(shǐ)刀軸與曲麵離(lí)散點(diǎn)的間(jiān)距,識別無幹涉刀軸空間(jiān)。針對無幹(gàn)涉刀軸空(kōng)間為(wéi)空(kōng)集的刀觸點進行幹涉刀軸修正,並利用投影法優化(huà)計算效率。加工結果表明建(jiàn)立的(de)五軸數控刀軌可(kě)實現加工幹涉,同時投影法有效(xiào)減(jiǎn)少參與幹涉(shè)檢測檢測額的曲(qǔ)麵離散點數量,提高計算效率(lǜ)。
關鍵詞:複雜曲麵;五軸加工;點雲模型;無幹涉刀軸
1、引言(yán)
隨著 CAD/CAM 技術的發展,複雜曲麵零件(jiàn)被(bèi)廣泛應用於(yú)能源、化工、航空航天等領域,製造(zào)此類零件(jiàn)常選用五軸數控加工。相較於傳統的三軸加(jiā)工(gōng),五軸數控技(jì)術可以提供更豐富的(de)刀具姿態,增加刀(dāo)具的加工範圍,減少反複裝夾(jiá)產(chǎn)生的人為誤差。但豐富的刀具(jù)姿態增加(jiā)了刀軸規劃的(de)難度,刀軸矢量沿刀軌不斷變化,刀具易(yì)與工(gōng)件發(fā)生幹涉。加工幹涉可(kě)分為局部幹涉和全局幹涉兩種,局部(bù)幹涉是指刀具端部出現過切,全局幹涉是指刀杆和工(gōng)件等發生(shēng)碰撞。幹涉現象(xiàng)不僅會降低零件質量(liàng),還可能使刀具斷裂(liè)失效。因此,加工過程無幹涉是優質五軸數控刀軌的重要指標。對於局部(bù)幹涉,刀具直徑是避免幹涉的關鍵因素,文獻利用遺傳(chuán)算法確定避免局部幹(gàn)涉的最佳(jiā)刀具尺寸。對於全局幹涉,研究重點在(zài)於(yú)判斷刀具柱麵和工(gōng)件表麵是否相交。文獻通過離散 B 樣條來判斷複雜(zá)曲(qǔ)麵(miàn)相交,文獻利用包圍盒刀具模型和八叉樹(shù)工件模型來進行幹涉檢測。文獻(xiàn)利用可視錐(zhuī)方(fāng)法生成無幹涉刀軌(guǐ),文獻將可視錐(zhuī)與(yǔ)刀具可(kě)達方向(xiàng)錐相結合,減少計算時長。為進一(yī)步提高計算效率,文獻(xiàn)采用(yòng)顯(xiǎn)卡計算的可視圖來規劃無幹涉刀軸,文獻根據無幹(gàn)涉刀軸空間確(què)定裝夾工件的最佳方位。複雜曲麵的(de)精加工刀具多為球(qiú)頭刀,其加工幹涉多為全局幹涉。隨著加工要求的不斷(duàn)提高,刀軸矢量所(suǒ)受的約束逐漸增加。利用點雲模(mó)型建立無幹涉刀軸空間,為後續刀軸規(guī)劃奠定基礎。
2、無幹涉刀軸空間
在數控程序中,刀軌曲線被視為一係(xì)列刀觸點。為保證整體刀軌無(wú)幹涉,需確定任一刀觸點的無幹涉刀(dāo)軸空間。球頭刀在任一刀觸點處的(de)旋轉中心為刀位點,因此(cǐ)初始刀軸空(kōng)間可視(shì)為以刀位(wèi)點為圓(yuán)心,刀具杆長為半徑的球(qiú)狀空間。初始刀軸空間內包(bāo)含無數的刀軸矢量,無法依次(cì)對其進行幹涉檢測。為從(cóng)初始刀(dāo)軸空間內提取(qǔ)無幹(gàn)涉空間,可根據曲(qǔ)麵法向(xiàng)建立等間距(jù)的陣列平麵和等夾角的旋轉平麵,兩組平麵與初始刀軸空間的球麵相交生成的經緯曲線,將經緯線交點與刀位點(diǎn)的連(lián)線(xiàn)作(zuò)為待測(cè)刀軸,如(rú)圖 1所示。待測刀軸將初始刀(dāo)軸空間離散為錐狀(zhuàng)子區(qū)域,若(ruò)存在待測刀軸與工件產生幹涉,則認為相(xiàng)鄰子區域是(shì)幹涉的;若標識子區域的待測刀軸均滿足(zú)無幹涉要求,則認為該區域(yù)內的刀(dāo)軸矢量是可行的。
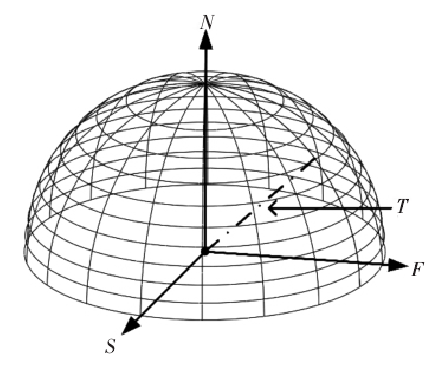
圖1:初始刀軸空間
2.1、全局(jú)幹涉檢測
為判斷待(dài)測刀軸(zhóu)是否發生幹涉,需對其進行幹涉檢測。幹涉檢測的本質是計(jì)算刀軸矢量與工件表麵的(de)間距,而複雜曲麵難以用解析公式(shì)直接表示。為(wéi)解決該問題可利用三角網格離散工件表麵(miàn),提取網格節點生成加工曲麵的點雲模型,計(jì)算(suàn)待測刀軸矢量與任一曲(qǔ)麵離散點的間距即可實現(xiàn)幹涉檢(jiǎn)測。假設刀位(wèi)點為 PC(x1,y1,z1),刀具端(duān)點為 PE(x2,y2,z2),被檢測的(de)曲麵離散點為 PS(x3,y3,z3),如圖 2 所示(shì)。
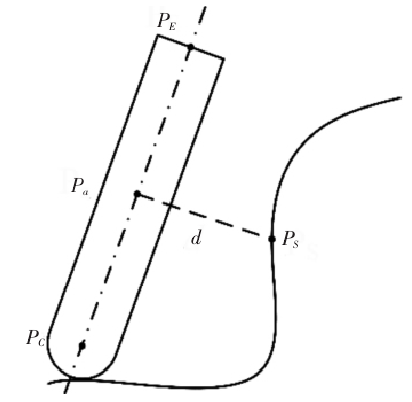
圖2:幹涉檢測
刀軸(zhóu)上的點(diǎn)可表示為 Pa(xa,ya,za):
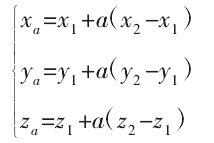
其(qí)中,a>0,Pa與曲麵離散點 PS的距離可表示為:
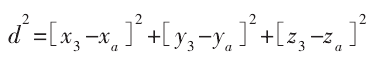
為(wéi)檢測幹涉,需計算 d 的最小值,此時式(2)滿足:
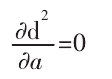
根據公式(3)可(kě)計(jì)算參數 a:
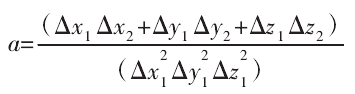
其中,△x1=x2-x1,△y1=y2-y1,△z1=z2-z1
將(jiāng)式(4)代入式(2)~式(3)即可計算刀軸矢量與曲麵離散點的間距,遍曆初始刀(dāo)軸空間內(nèi)的曲麵離散點,提取待測刀(dāo)軸矢量與曲麵離散點的最小間距。若最小間距小於刀具半徑,則表示該刀軸矢量下刀具會與工(gōng)件發生幹涉;反之則(zé)說(shuō)明刀(dāo)軸矢量無幹涉。依次檢測所有(yǒu)的待測刀軸矢量,提取由無幹涉刀軸矢量(liàng)標識的子區域,構建單個(gè)刀觸點的無幹涉刀軸空間。
2.2、幹涉(shè)刀軸修正(zhèng)
在構建無幹涉刀軸(zhóu)空間的過程中,待測刀軸矢量間存在(zài)一定間距。若刀觸點(diǎn)位於較為封閉的區域,此時無幹涉刀(dāo)軸空間可能為空集,為避免該現象需對已知的幹(gàn)涉刀軸矢量進行修正。將與刀軸矢量(liàng)發生幹涉的曲麵離散點標記為幹涉點,若刀(dāo)具與工件發生嚴重幹涉,則相應的刀軸矢量必然擁有大量的幹(gàn)涉點;反之幹涉點(diǎn)的數量較少。從幹涉刀軸空間內提取幹(gàn)涉點最(zuì)少的刀軸矢量,將其作為修正(zhèng)目標 T。修(xiū)正幹(gàn)涉刀軸,如圖 3 所示。
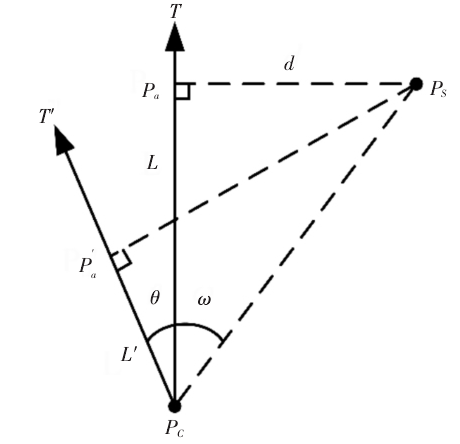
圖3:修正幹涉刀(dāo)軸
提取與幹涉刀軸 T 最近的曲麵離(lí)散點 Ps,建立的修正平麵,如圖 3 所示。Pa和 Pc的距離為 L,幹(gàn)涉刀(dāo)軸和曲麵離(lí)散點的夾(jiá)角ω 可表示為(wéi):
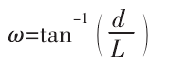
若完成(chéng)刀軸修正,曲麵離(lí)散點 Ps與修正刀軸 T′的間距可表示為 R+ε,R 表示刀具半徑,ε 表示刀具和工件間(jiān)的(de)微量間距,避(bì)免修正後(hòu)的刀具(jù)和工件臨界接觸(chù)。此時 P′a和 Pc間的距離L′可(kě)表示為:
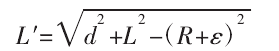
修正(zhèng)角度 θ 可表示為:
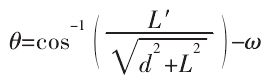
將(jiāng)幹(gàn)涉刀軸 T 和曲麵離散點 Ps的夾角增加 θ 即可生成修正刀軸 T′,修正後的刀軸矢量(liàng)仍需進行幹(gàn)涉檢測,避免修正過程產生新的(de)幹(gàn)涉點。若存在新的幹涉(shè)點,可重複上述步驟直至生成無幹涉刀軸。為避免陷入無限循環,可限(xiàn)製循環次數(shù),若多次循環後仍無法生成無幹涉刀軸,可減少刀具直徑以增加刀具和工件的間距。
2.3、投(tóu)影法優化
在上述算法中,參與檢測的曲麵離散點數量是決定計算效(xiào)率的關鍵。若減少離散密度會降低幹涉檢測的精度,因此需在保持離散密度的前提下減少參與檢測的曲麵(miàn)離散點。投影法是識別潛在幹涉區域的有(yǒu)效手段,若刀軸矢量引發幹涉,離散點必然(rán)侵(qīn)入刀具內部,此時離散點投影被刀具投影覆蓋(gài),如圖 4 所示。
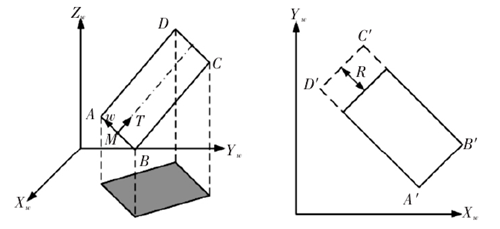
圖4:刀具投影
在工件坐標係(Workpiece Coordinate System)內選取 XwYw麵作(zuò)為投影平麵,Zw軸(zhóu)負向為投影方向。為簡化刀具投影的計算過程,可(kě)將刀(dāo)具表示的矩形麵,如圖 4 所示。M 為刀心點,T 為刀軸(zhóu)矢量,w 與 T 正交同時平行(háng)於 XwYw平麵。AB 間距為(wéi)刀具直徑,BC 間距為刀具杆長,矩形(xíng)麵四點坐標可分別表示為:
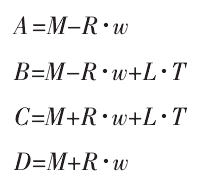
將四點的 Zw軸坐標設為 0 即可(kě)獲得刀具在 XwYw平麵內的投影 A′B′C′D′,但(dàn)該投影忽略了刀具端麵的影響。為(wéi)提高計算精度(dù),可將刀(dāo)具投影沿刀軸方向延伸 R 個單位長(zhǎng)度,增加投影的覆蓋麵積。若曲麵離散點的投影 P 位於刀具投影之內,P 點必然滿足:
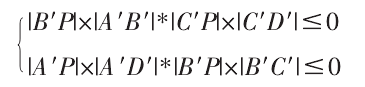
位於刀具投影內的曲麵離散點是潛(qián)在的幹涉區域,需進行幹涉檢測;刀具投影外的曲麵離散點不(bú)必參與幹涉(shè)檢測。
3、刀軸光順優化
在實際加工中,刀軌不能從無幹涉刀(dāo)軸空間內任意選用刀軸矢量,因為刀軸整體需具備良好的一致性,避免刀軸突變,保持機床穩定運(yùn)動。為實現上述目標,需對(duì)刀軸進行光順優化。將無幹涉刀軸空間最小的刀觸(chù)點作為刀軸規劃的起始點,指定該點的刀軸矢量,以最小角度變化為原則規劃相鄰(lín)刀軸,遍(biàn)曆刀觸點完成初始刀軸(zhóu)規劃。單個刀觸點的無幹涉刀軸空間內可能存在多個(gè)刀軸矢量滿足最小角度變化要求,因此初始刀軸軌(guǐ)跡存在多種可(kě)能(néng)。若刀軸軌跡具有較好的光順性,其掃掠麵積較小,因(yīn)此可利用刀軸(zhóu)掃掠麵積判斷刀軌的光順性(xìng)。利用 ci、ti、ci+1、ti+1四點表示相(xiàng)鄰刀(dāo)軸(zhóu),如圖 5 所示。
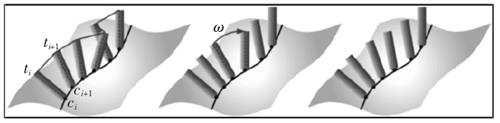
圖5:刀軸光順優化
相鄰刀軸間的掃掠麵積可(kě)近似表示為:
若刀軌共含有 N 個刀觸點,則刀軌整體的掃掠麵積可表示為:
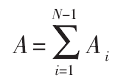
計算初始刀軸軌跡的掃掠麵積,提取掃掠麵積最小的刀軸軌跡。若(ruò)結果不唯一,可根據角速度方差進一(yī)步對(duì)刀軸軌跡進行篩選。在相同的掃掠麵積下,刀軸的角速度存在差異,光順(shùn)的刀軸(zhóu)軌跡應具備更小(xiǎo)的(de)角速度波(bō)動。因為相鄰刀軸的(de)間距極小,因此角速度可近(jìn)似表示為:
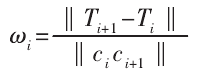
角速度的波動可用角速度方差表示:
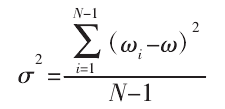
式中:ω—平均(jun1)角速度,方差最小的刀軸軌跡具備更理想的光順性。
4、驗(yàn)證(zhèng)實例
建立的工(gōng)件模型,將工件表麵離散為單位長度 1mm 的三(sān)角網格,提取網格節點(共計 8403 個)建立工件點雲模型,如圖 6 所示。利用 UG NX 軟件生成刀軌曲線,按方法構建任一刀觸點的無幹(gàn)涉(shè)刀軸空間。以刀(dāo)位點(7.0283 24.4214 12.5602)為例,其無幹涉刀軸空間,如圖 7 所示。從該點的無幹涉和幹涉刀軸空間內分別選(xuǎn)取刀(dāo)軸矢量(liàng)生成刀軌,在 UG 內對刀軌進行仿真分析,結果如圖 8 所示。

圖6:工件點雲模型
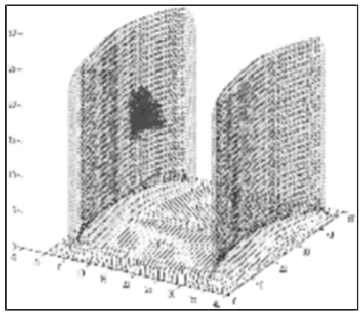
圖7:無幹涉(shè)刀(dāo)軸空間
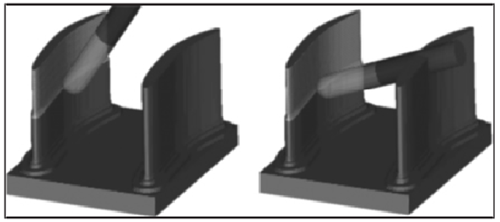
圖8:無幹涉(shè)和幹涉刀(dāo)軸仿真
仿真結(jié)果表明(míng)無幹(gàn)涉刀軸空間內的刀軸與(yǔ)工件表麵存在明顯間距,加工過程無幹(gàn)涉;幹涉刀軸空間內的刀(dāo)軸矢量使刀具侵入(rù)工件內部,該刀軸(zhóu)無法應用於實(shí)際加工。對幹涉刀軸進行修正處理,並(bìng)利用投影法優化修正過程,如圖 9、圖 10 所(suǒ)示。修正後(hòu)的刀軸矢量可有效(xiào)避免幹涉,在投影法約束下,參與幹涉檢測的曲麵離(lí)散點(diǎn)減(jiǎn)少至 644 個,幹涉檢測量大幅減少。
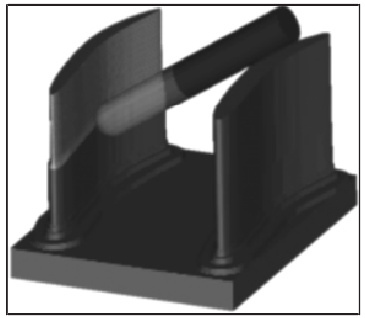
圖9:修正刀軸仿(fǎng)真
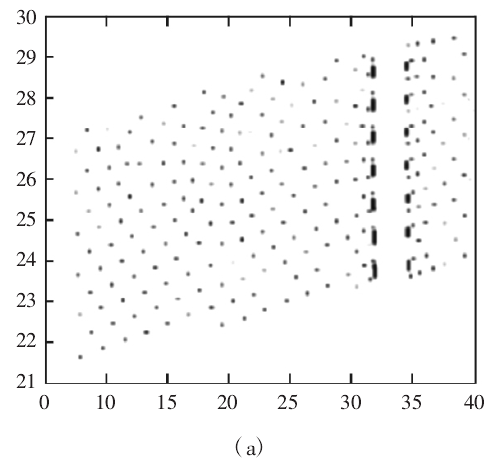
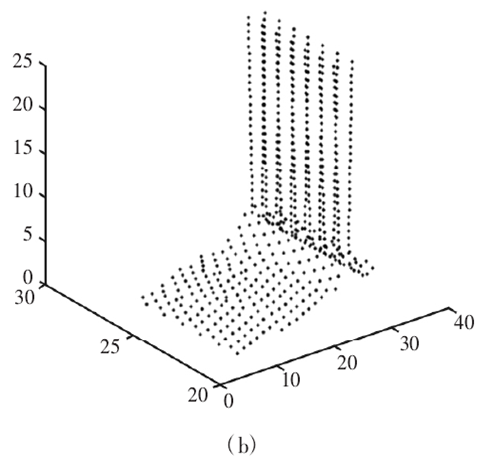
圖10:刀具投影(yǐng)內的曲(qǔ)麵離散點(diǎn)
利用五軸數控加工中心將修(xiū)正後的無(wú)幹涉刀軌應用於實(shí)際加工,如圖 11 所示。

圖11:加工結(jié)果
在實際加工中,刀杆(gǎn)與工件保持(chí)安全間距,加工過程穩定無幹涉。由仿真結果可知(zhī)相較於修正(zhèng)刀(dāo)軸,無幹(gàn)涉刀軸與工件的間(jiān)距(jù)更充裕,因此利用無幹涉刀軸空(kōng)間生成的刀軌亦可避免加(jiā)工幹涉。
5、結論
(1)利用方法生成的無幹涉刀軸空間規(guī)劃刀軸矢量可保證加工過程的可靠性,對原先幹涉的刀(dāo)軸矢(shǐ)量(liàng)進行修正處理也可實現幹涉(shè)避讓;
(2)點雲模型共有 8403 個(gè)曲(qǔ)麵離散(sàn)點,初始刀軸空間內包含離散點 6806 個,位於刀具投影(yǐng)內的曲麵離散點(diǎn)為 644 個,投影法有效減少了參與幹涉檢測的曲(qǔ)麵離(lí)散點數量(liàng),提高了計算效率。
投稿箱:
如果您有機床行業、企業(yè)相關新聞稿件發表,或進行資(zī)訊合作,歡迎聯(lián)係本網編(biān)輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業(yè)相關新聞稿件發表,或進行資(zī)訊合作,歡迎聯(lián)係本網編(biān)輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





