【技（jì）術淺析】數控機床軸承結構振（zhèn）動諧響應及疲勞壽命研（yán）究-功能部件網（wǎng）-數控機床市場網

您現在的位置：功能部件網> 技術前沿（yán）>【技術淺析】數控機床軸承結構振動諧響應及疲勞壽命研究（jiū）

【技術淺析】數（shù）控機床軸承結構振動諧響應及（jí）疲勞壽命（mìng）研究

2020-11-9 來源：貴州師範大學機械（xiè）與電氣（qì）工（gōng）程學院等作者：沈（shěn）明明（míng），李榮，劉祖國（guó），湯（tāng）耿

摘要: 以（yǐ）數控機床用的（de）深溝球軸承為研究對象，分析其運轉中的振型及結構疲勞壽命。首先通（tōng）過Solidworks 建立了深溝球（qiú）軸承的三維模型，利用ANSYS 對軸承進行模態及（jí）諧響應分析，獲得軸（zhóu）承在固（gù）有振動頻率以（yǐ）及在各階次頻率下（xià）的固有振（zhèn）型變化，同時借助有（yǒu）限元諧響應分析，確定了對軸（zhóu）承（chéng）影響最大的（de）模態頻率（lǜ）。其次利用 ANSYS 中的 Faigue 模塊對軸承進行了疲勞壽命研究，通過結合材料的 S-N 曲線理論以及 Hertz 接觸（chù）理論（lùn），對軸承的疲勞壽命（mìng）進行了預（yù）估（gū）分析。仿真結果表明: 在滿足軸承強度工況下，固有頻率 1125Hz 為結構（gòu）共振最大點，且軸承的壽命範圍為5937． 7 ～ 1 × 106次，為後續軸承結構優化提供參考。

關鍵詞: 深溝球軸承; 模態振型; 振動諧響應; 疲（pí）勞敏感性; 疲勞壽（shòu）命

0、引言

隨（suí）著製造工業技術的快速發展，數控（kòng）機床被廣泛（fàn）應用（yòng）於關鍵零部件的加工製造，而主軸係統（tǒng）中軸承結構則是其運轉的關（guān）鍵部件。軸承（chéng）作為重大機械傳動中的重要支（zhī）承傳動部件並且能夠減少摩（mó）擦，因此軸承的好（hǎo）壞直接（jiē）關係到機床加工精度和工作效率等性（xìng）能。

同時軸承的振動疲勞破壞一直是影響機械結（jié）構（gòu）運行的關鍵（jiàn）因（yīn）素。近幾年（nián），國內外學者對軸承結構的運行狀態及振（zhèn）動（dòng）變化進行了研究分析，文獻通過利用有（yǒu）限元法對航空圓柱滾子軸承（chéng）的溫度場及（jí）應力分（fèn）布進行仿真分（fèn）析（xī）同時還對軸承（chéng）熱力耦合下的疲勞壽命進行研究，文獻通過建立接觸模型，提出了（le）一種（zhǒng）載荷計算分布模型對深溝球軸承內部載（zǎi）荷序列與（yǔ）壽命進行計算。文獻中HOUPEＲT 分析了滾動軸承在（zài）運行過程中對（duì）疲勞壽命造成影響的因（yīn）素（sù），上述研究都（dōu）取得了一定的效果，但都隻是單一（yī）的針對軸承的溫度場及載（zǎi）荷序列進行研究。針對（duì）軸承振動諧響應與壽命的（de）研究的報道並不多。

因此，本文以數控機床用深溝球軸承（chéng）為研究對象（xiàng），通（tōng）過對軸承結構進行參（cān）數化建模，分析軸承靜（jìng）應力及模態振型變化。結合諧響應分析模塊，利用模態疊加法分析深（shēn）溝球軸內圈的（de）諧響應變化（huà）。同時利用材（cái）料的S-N 曲線及（jí）疲勞靈敏度曲線對軸承進行了（le）恒定載荷工況（kuàng）下的（de）疲勞壽命研究，為數控機床主軸係統軸承振動疲勞分析及優化提供了參考。

1、深溝球軸承有限（xiàn）元分析

1.1、深溝球軸承靜應力分析

軸承結構在運行過程（chéng）中其結構的振型變化將會直（zhí）接對結構的性能造成一定的影響，因（yīn）此結構的振動特性決定（dìng）了結構在不同（tóng）載荷（hé）情況下的（de）響（xiǎng）應變化，所以對（duì）結（jié）構進行模態振型仿真分析具（jù）有重要意義。

由於在（zài） ANSYS 中的建模工具並不成熟，因此本文利用 Solidworks 建（jiàn）立（lì）了深溝球軸承（chéng）的參數化（huà）三維模（mó）型（xíng），通過轉（zhuǎn）變模型（xíng）的格式聯立到 ANSYS 中進行分析，在進行（háng）分析時需要對結構的材料進（jìn）行定義，本文分析時主要是利（lì）用有限元的方法進行利用，因此本文設定（dìng）結（jié）構的材料都為軸承鋼，其泊鬆比為 0.3，密度為7810kg/m3，彈性模量為210GPa，設定完（wán）材（cái）料參（cān）數後，需要對結構的網格進（jìn）行定義，因為在仿真分析時結構的網格是否合格直接影響到結構的分析精度，雖（suī）然係統有手動劃分（fèn）網格的功能，針對複（fù）雜的（de）幾（jǐ）何結構（gòu）大多采用自動劃分功能，通過設定網格為 Fine 劃分得到如圖 1 所示的深溝球軸承有（yǒu）限元網（wǎng）格模型，其中網（wǎng）格節點為10536，單元數為3950，網格質量為良好。

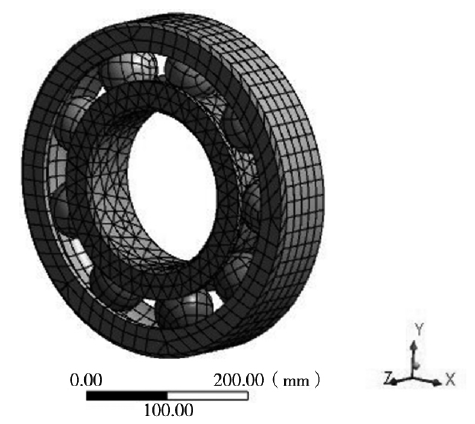
圖1 . 深溝球軸承有（yǒu）限（xiàn）元網格（gé）模型

1.2、邊（biān）界條件設定（dìng）

在軸承運行過程中，其中內圈是與轉子軸接觸，外圈則一般是與固定件接觸在一起，因此在設置深溝球軸承約束條件時將圖 1 中軸承外圈設定為固定（dìng）約束，內圈（quān）設定為旋（xuán）轉（zhuǎn）約束（shù），本文轉速（sù）設（shè）置為10000rpm。

1.3、有限元靜應力結果

通過設定完結構的邊界約束條件和網格模型後，在靜應（yīng）力模塊中選中變形模塊及平均應力模塊，分析解算得到如圖 2a 所示的靜應力總變形和圖 2b 所示（shì）的軸承平均應力雲圖。

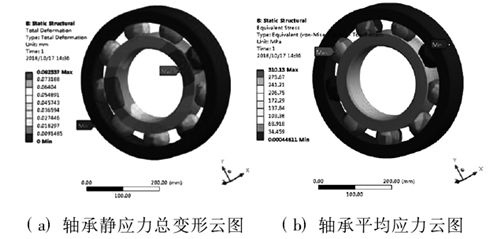
圖2 . 軸承靜應力應變形雲圖

從圖 2 中的雲圖可知（zhī），深溝球軸承的最大變形量為 0.083mm，軸承的最大平均應力為 310MPa，由（yóu）於在設定材料時，定義的軸承材料為是軸承鋼，彈性模量為210GPa，屈服強度為 1667MPa。根據第 4 強度理論（lùn）可以（yǐ）計算材料是否符合強度要求，強度公式為:

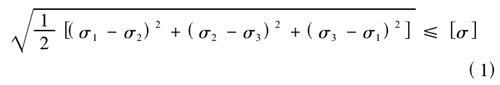
式中，σ1，σ2，σ3為 3 個法向的應力。在計算材料的許用應力時，安全係數一般（bān）取的是 1.5，通過許（xǔ）用應（yīng）力公式計算可得到。許用應（yīng）力公式（shì）:

通過結合式( 1) 與式( 2) 可以計算軸承的許用應力為 1111.3MPa。結合圖 2 應（yīng）力雲圖可得（dé） 310MPa≤1111.3MPa，所以創建的軸承結（jié）構的強度滿足設計分析要求。因此在（zài）後續的諧響應分（fèn）析及疲勞壽（shòu）命的分析中可以（yǐ）獲得軸承具有參考價值的數據參數，為後期軸（zhóu）承的改進提供有效的優化方案。

1.4、深溝球軸承模態（tài）分析

在繪製深溝（gōu）球軸承結構的三維模型時，忽略掉一些對結構影響（xiǎng）不（bú）明顯特征，這樣將能加快求解時間。由於軸承產生破壞的階段主（zhǔ）要是在負載工況下發生的，所以本文在繼承靜應（yīng）力分析的基礎上對軸承的（de）模態振型進行研究（jiū）分析。設定模態階數為 6 階，得到軸（zhóu）承的前 6 階模態固有頻率如表 1 所示。

表 1 深溝（gōu）球軸承前 6 階振型

結（jié）合 1.1 節的模態有限元分析可知，結構在運轉過程中，主要（yào）是（shì）低階模態的振型對結構（gòu）的破壞較為關鍵，因此在有限元分析時不（bú）需要考慮到（dào）高階模態的振（zhèn）型，因此選取了軸承的前 6 階進（jìn）行模態振（zhèn）型分析，模態分析結果如圖 3 所示。

從圖 3 中模態振型變化中可以得到，軸承的低階模態振型變化量較大，主要對內圈的軸向振動變形較為明顯，其中在模態 2 階中振動變形（xíng）達到最大，最大約為 20mm，可以判定在內圈與滾（gǔn）珠接觸的部位較為薄弱，為提高軸承的（de）可靠性及壽命（mìng）可以在與軸承的內圈與滾珠接觸部（bù）位提高加工精度或對滾道進行特殊處理，以提高滾道的光（guāng）滑度及強度。對此在本文的（de）後續諧（xié）響（xiǎng）應分析中主要對（duì）軸承結構的內圈進行分析（xī），為後續軸承結構的優化及加工提供參考。

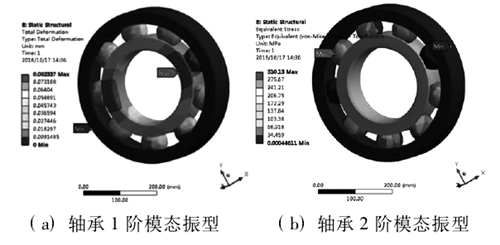
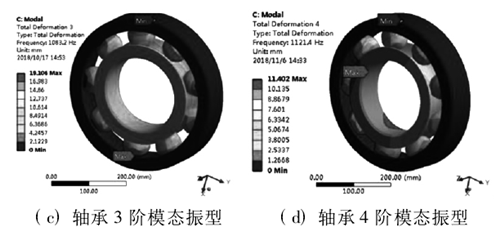
圖3 . 深溝球軸承前6階模態（tài）振型雲圖

1.5、深溝球軸承諧響應分析

結構的諧響應分析主要是（shì）對載荷在（zài）不同頻率（lǜ）下的振動響應，直接與結構的載荷有關，而（ér）模（mó）態分析的（de）結果隻是單一（yī）的（de）獲得在某一頻率下的（de）振型變化，並（bìng）不能獲得在不同頻率（lǜ）下的變形。因此結合（hé）模態分析結果搭建諧響應分析來提高諧響應分析結果的可用性，同時通過（guò）諧響（xiǎng）應分析還可為軸承的疲勞破壞和共振破壞具有一定預（yù）測作（zuò）用，對此本文通過模態疊加法開展軸承結構的諧響應分析，在求解中的設置（zhì）條件為:

① . 設置軸承的邊界條件參考 1． 2 節中的條件。

② . 從圖 3 的模態雲（yún）圖和（hé）表 1 中（zhōng）的前 6 階固有頻率可知（zhī），軸承的第6階頻率為 1285.3Hz，對此（cǐ）設置諧（xié）響應的分析範圍為（wéi）0～1500Hz，同時為了（le）提（tí）高計算結果的（de）精（jīng）確（què）性設置求解步數為 100 步對應的有100個解。由（yóu）模態分析可知變形主要（yào）發生在軸承的內圈，因此在諧響應分析中主要選取內圈進行（háng）了諧響應分析（xī），通過求解（jiě）計算獲得了內圈沿 X、Y、Z 方向的位移變化情況，如圖4所示。

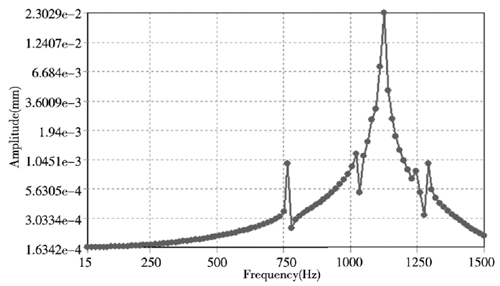
(a) X 方（fāng）向

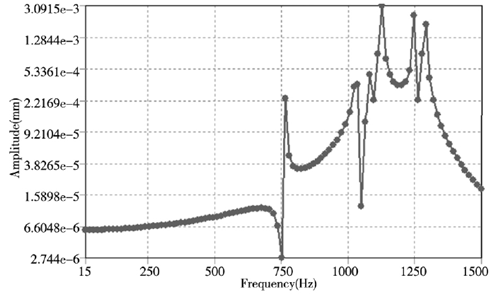
(b) Y 方向

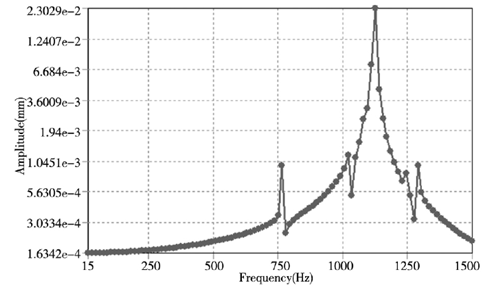
(c) Z 方向

圖4 . 軸承（chéng）內圈（quān）結構 X、Y、Z 方向位移響應曲線

從圖 4 中的軸承內圈（quān）結構 X、Y、Z 方向位移響應曲線可知，軸承結構的位移響應隨著頻率的增（zēng）加而增加，呈正相關。而在 X、Z 方向的位移在模態 5 階( 約1125Hz) 時達到最大位移變化，最大變化量為0.023mm，而對於Y方向的位移變化量（liàng）則（zé）較小為0.003mm，這要是軸承在 Y 方向上主要是受（shòu）到徑向的力，而 X 和 Z 方向還會受到（dào）沿 X 軸的軸向（xiàng）力，因此在 X和 Z 方向的位移較大（dà），雖然 Y 方向（xiàng）的最大位移量沒有X 和（hé） Z 方向的大，但在頻率（lǜ）從1階到 6 階（jiē）範圍內位（wèi）移變形量較為均勻，因此造成的破壞不容忽視。通過對軸承的（de）諧響應的分析可知（zhī） X、Y、Z 方向所造成（chéng）的（de）影響都不可忽視，在後期優化和加工工藝中通過設計特定的工裝（zhuāng）來優化軸承的結構，諧響應分析結果也為後期同類產品的優化提供參考。

2、深溝球軸承疲勞壽命分（fèn）析

2.1、Hertz 接觸應（yīng）力計算

在分析軸承應力疲勞壽命時（shí），應先分（fèn）析軸承的應力，同時找到軸承的最大應（yīng）力區域。對此依據 Hertz接觸應力理論對軸承的應力進行分析，在接觸應力中（zhōng）接觸載荷 Q 與彈（dàn）性趨近量 δ 滿足下式:

式（shì）中，K 代表接觸體之間的載（zǎi）荷變形係（xì）數，一般與接觸（chù）體的材料及外形有關（guān）。

在軸承工作過程中，由於內外滾道（dào）的直徑差異，滾道對滾珠的接觸應力也有所不同（tóng），同時 2 滾道的法向趨近量等於滾珠分別與內外滾道趨近量之和，滿足下式:

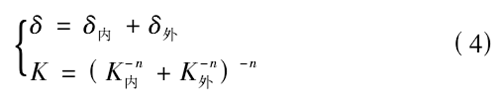
對於深溝球軸承，式（shì）( 3) 和式( 4) 中的 n 係（xì）數一般取 1.5。通（tōng）過 Hertz 理論分析球軸承的接觸問題，其最（zuì）大的接觸應力為:

式中，a 表示接觸橢圓的長半軸; b 表示接觸橢圓短半軸。

通過上式理論分析（xī）在結合圖 2 所示的靜應力仿真分析雲圖可知，接觸處的正壓力主要為滾珠與內外（wài）圈接觸部位，其值（zhí）沿曲麵軸向與法向（xiàng）變化（huà），與（yǔ）式( 5) 的接觸理論分析一致。

2.2、疲勞分析

采用 ANSYS 聯合仿（fǎng）真對深溝球軸承進行疲勞計算，在分析軸承（chéng）靜應力的基礎上聯合（hé） Faigue 模塊進行分析，在分析設置（zhì）中為了提高分析的有效性，在（zài）搭建的Faigue 模塊（kuài）中設置疲勞強度因子為 0.8，通過反複模擬分析取最小基本載荷變化（huà）幅度和最大基本載荷幅度分別（bié）為 10% 、300% ，由此獲得軸承結構的疲勞敏感性曲線如圖 5 所（suǒ）示。

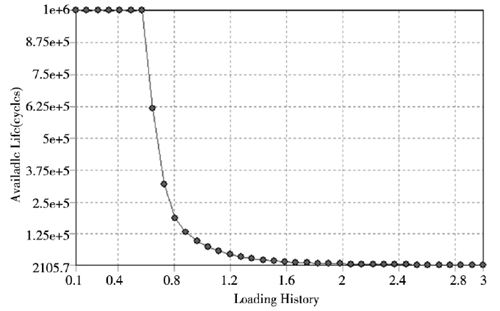
圖5 . 深溝球軸承疲勞敏感性曲線

在設定軸承的疲勞安全因子分布雲（yún）圖命令，可獲得如圖 6 所示的安全因子分布雲圖（tú）。從圖 6 中可以得到，本文選取的深溝球軸承最小安全影響（xiǎng）因子為0.27795，最容易（yì）發生疲勞破壞的部位主要是軸承內圈，這與實際工況下的破壞一致，為提高壽命（mìng），在（zài）後續的優化設計可以改變內圈材料及內圈與滾珠（zhū）接觸處的尺寸（cùn）參數來提高軸承內圈的使用壽命。由圖 5 中的敏感性曲線可知，軸承在載（zǎi）荷變（biàn）化幅度為 10% ～ 60% 範圍內對軸承的壽（shòu）命影響不大，但在載荷變化幅（fú）度（dù）超（chāo）過200% 時則直接對軸承造成破壞（huài）不滿足設計要求，通過上述（shù）分析（xī）可為軸承在設計中（zhōng）驗證軸承疲勞壽命是否滿足要求提供參考。

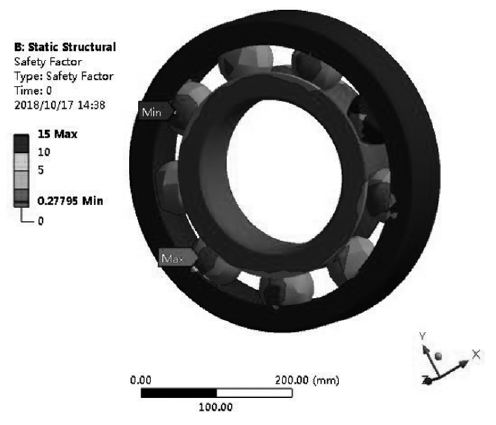
圖6 . 深溝球軸承（chéng）安全因子雲圖

2.3、振動疲勞壽命計算

一般情況下軸承的循環壽命較高（gāo），屬於低應力高周疲勞，通過采（cǎi）用（yòng）全壽命分析方法，即 S-N 曲（qǔ）線對（duì）軸承進行疲勞壽命（mìng）分析計算，通過上述的對軸承的材料進行定義得到軸承的 S-N 曲線如圖 7 所示。

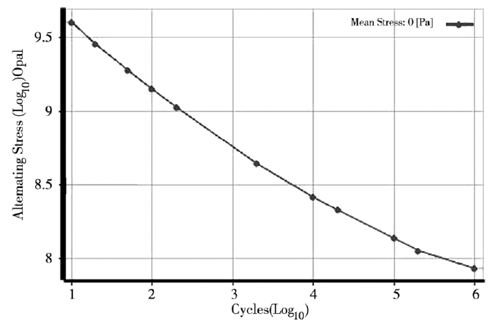
圖7 . 軸承 S-N 曲線

在有限元（yuán）分析中，設置雨流循（xún）環計數的方法對不規（guī）隨（suí）機的載荷時（shí）間曆程曲（qǔ）線進行轉化成一係列恒定幅值的載荷，本文設定的載荷（hé）為恒定幅值載（zǎi）荷對軸承進行疲勞壽命預估，如圖 8 所示。

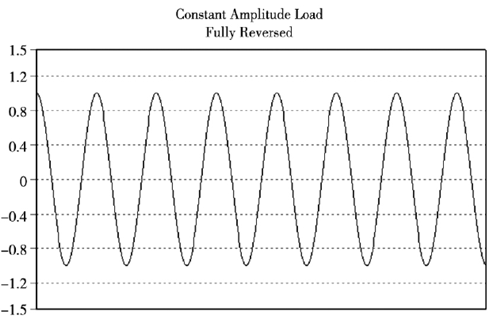
圖8 . 恒定幅值載荷

其中疲勞壽命（mìng）公式如下:

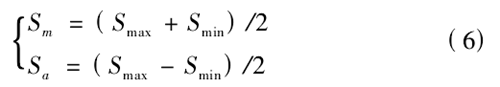
式中，Sm表示平均（jun1）應力; Smax表示最大應力取310MPa; Smin為最小應力取 34MPa; Sa表示交變應力幅。

其（qí）中平均應（yīng）力的修正應力公式（shì）為:

式中，Sn為平均（jun1）應力 Sm的修正應力;

由圖 7 所示的軸（zhóu）承 S-N 曲線來計算曲線間的斜率h，可以假設 S* N = C 為直線，利用最小二乘法來擬合出最優的直線方程，擬（nǐ）合得到如（rú）下方（fāng）程:

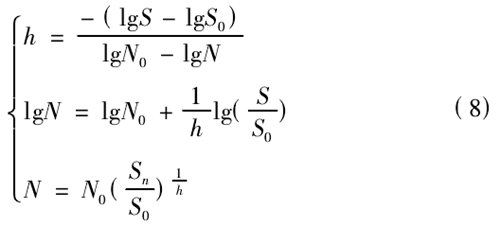
式中，N0表示循環次數，N0= 1 × 106; S0表示（shì）在 N0=1 × 106時的（de）應力；

結合圖7可知 lg N0= 6，lg S0= 7.88，lg N = 3，lg S = 8.75 ，通過計算可（kě）得到 h 值為－ 0.29。其（qí）中平均應力 Sm的修正應力為：Sn=153.8MPa 將其帶入式(8) 中可（kě）得軸承疲勞壽命 N≈8.74 × 104次。結合圖5的（de）敏（mǐn）感性曲線圖可知軸承的載荷變化幅度在 10% ～60% 範圍內，因此對（duì）軸承的壽命影響不大，滿足疲（pí）勞壽命設計要求。

同時借助有（yǒu）限元 Faigue 分（fèn）析模塊，對深溝球軸承循環次數的疲勞壽命進（jìn）行求解計算（suàn），可獲得圖 9 所示的軸承疲勞壽命雲（yún）圖。

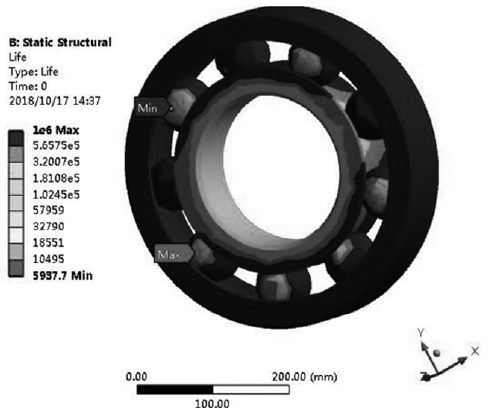
圖9 . 深（shēn）溝球軸承疲勞（láo）壽命( 循環（huán）次數（shù）)

由圖（tú） 9 中的疲勞（láo）壽命分（fèn）析雲圖可知，當工況條件為轉速（sù）設置 10000rpm 時，軸承（chéng）的壽命範圍為（wéi） 5937.7 ～1×106次，壽命較小處為軸承的滾珠外側和軸承內圈部位，但是壽命薄弱處較少（shǎo），其有限元（yuán）疲勞壽命分析與理論計算（suàn）結果大體一致，且有限元分（fèn）析法能夠將疲（pí）勞破壞點清晰直觀的（de）表（biǎo）示出來，由此可知通過利用有限元法對結構做疲（pí）勞壽命分析是可靠的，可為後續結構優化提供參（cān）考。

3、結論

深溝球軸有（yǒu）限元靜應力及模態分析，能獲得結（jié）構的固有頻率及振型變化，可為結構的諧響應及疲勞分析提供基礎（chǔ）。

(1)、結合有限元靜應力及模態分析結果，采用模態疊加法，搭建了軸承結構的諧響應分（fèn）析模塊，獲得了軸承內圈沿 X、Y、Z 方向上的位移響應曲線，得到了軸承在 X、Z 方向的位移在模態 4 階( 約1125Hz) 時（shí）達到最大位移變（biàn）化，最大變化量為 0.023mm;

(2)、通過利用材料的 S-N 曲線理論以及 Hertz 接觸理論開（kāi）展了軸承結構的疲勞壽命分析，在靜應力分析的基礎上，通過（guò） Faigue 模塊建立軸承結構的疲勞分析模型，理論（lùn）疲勞壽命為 8． 74 × 104次，與仿真分析結果大體一致，驗證了仿（fǎng）真計算的可行性，也為軸承結構的後續優化提供參（cān）考，加快研發（fā）進度。

投稿箱（xiāng）：
如果您有（yǒu）機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯係本網編輯部，郵箱：skjcsc@vip.sina.com

更多相（xiàng）關信（xìn）息

名企推薦

業（yè）界視點

| 更多

行業數據

| 更多

博文選萃

| 更多

數（shù）控機床（chuáng）