摘要:根據鐵路機車軸承的結構（gòu）特點, 綜（zōng）合考慮滾動軸（zhóu）承座及內外套圈的彎曲變形,本文（wén）建立了軸承載荷分布計算模型（xíng）。通過有（yǒu）限元分析計算, 給出了軸承實際載荷分布值, 並為軸承支座（zuò）的剛性設計提出（chū）了設計（jì）要求和建議（yì）, 為滾動（dòng）軸承的CA D 優化設計提（tí）供了切實可行的計算方法。

關鍵詞: 計算機輔助設計; 滾動軸承; 載荷分布（bù）

      傳統的軸承載荷計算, 視軸承支座及內外套圈為剛體, 因而（ér）存在著較大的（de）誤（wù）差. 實（shí）際上, 不論是軸承座或者內（nèi）外套圈都是（shì）;彈性（xìng）體, 受力後都要發生變形. 根據鐵路機車軸承的結構特點, 作者綜合考慮了滾動軸承座及內外套圈的彎曲變形（xíng）, 也考慮到滾動物承支座和內外套圈的（de）彈性後的計算是一個接觸問題( 包括點接觸和麵接觸) , 過程比較複雜. 為了（le）工程設計中的實用性, 需（xū）要尋求一個（gè）既能準確反（fǎn）映實際工況, 又便於工（gōng）程設（shè）計的簡化的計算模型。

     本文建立的軸承載荷計算模型則反映了這一點, 從而（ér）使設計計算結（jié）果更加符合實際工況. 通（tōng）過有限元分析計算, 給出了軸承實際載荷分布圖, 並為軸（zhóu）承支座的剛性設計提出了設（shè）計要求和建議, 為滾（gǔn）動軸（zhóu）承（chéng）的C A D 優化（huà）設計提（tí）供了切實可行的計算方法.

1 計算模型

      鐵（tiě）路機車軸（zhóu）承的實際（jì）工作情（qíng）況如圖1 (“) 所示. 為了便於工程應用（yòng）, 考慮到滾（gǔn）動軸承的內慈外套圈在額定工況下由於受熱膨脹等各種因素分別與機車輪軸和（hé）軸承座緊配合, 因此作如下假（jiǎ）設:

      a. 視內外（wài）套（tào）圈分別與軸和軸承座為（wéi）一體.

      b. 對受載滾子的剛度和外圈一支座聯合體與（yǔ）滾子接觸點的剛度經（jīng）綜合處理( 串聯) 後,視為一組彈性支撐, 如圖1 (b) 所（suǒ）示.

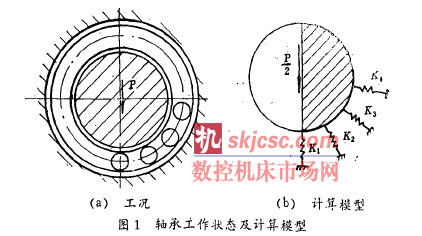
      通過經驗（yàn）公式1和有限元法分別（bié）求得滾子的剛度（dù）和外圈（quān）一支座聯（lián）合體與滾子（zǐ）接觸點的剛度（dù）, 並（bìng）經串聯計算得彈性支撐的剛（gāng）度( K I , K : , K : , K ; ). 圖1( a ) 中的P 是軸承的外載荷. 在圖1 (b ) 中, 由於考（kǎo）慮平麵問題, 載荷需左右對稱, 因（yīn）而（ér）載荷取P / 2 .

2 計算方法

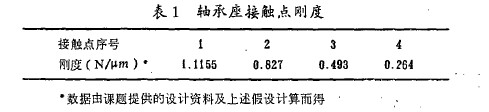
      以滾動軸承4 2 7 2 4.為例進行（háng）了載荷分布計算. 對於短圓柱體滾動體, 因（yīn）載荷在軸向看作均布, 故可作平麵問題考慮, 用有限元法求得外圈一支座聯合體與滾子接（jiē）觸點處的剛度. 相對於其它彈性體的剛度支座的剛度大得多, 故處（chù）理為線（xiàn）性（xìng）. 4 2 7 2 4 滾動軸承共有（yǒu）14 個圓柱滾子, 受載滾（gǔn）子數最多為7 個, 且左右軸對稱. 表1 所列為模型所示4 個接觸點（diǎn）的剛（gāng）度。

      滾子的剛度為非線性, 利（lì）用Pa lm gr e n 公（gōng）式可迭代求得。Pa lm gr e n 公式

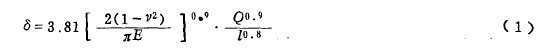
      其中δ 一變形量（liàng）( m m ) ; E 一彈性模量( N / m m 2 ) ; ,v一泊鬆（sōng）比;L一滾子有效接觸（chù）長度( m m ) ; Q 一滾子上的作用載荷( N ).

      由於公式（shì）(1) 中包含了滾子載荷Q , 因而實際的滾子剛度要在總的計算程序中經迭代計算而得.

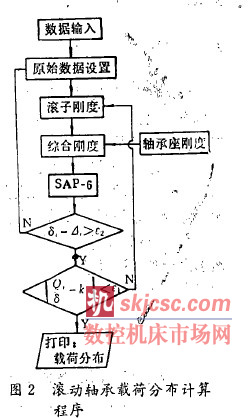
      滾動（dòng）軸承載荷分（fèn）布計算程序如圖2 所示. 輸入的原始數（shù）據主要包括軸承的幾何參數、軸承的總載荷p、原始遊隙△ 等. 初值設定指受（shòu）載滾子數的設定（dìng）和滾子剛度的設定. 首先幾設’定受載滾子數為（wéi）7 ( 最大可能受載滾子數), 然後依據判定條件判定; 滾子剛度按公（gōng）式(1) ,韶魄取平均載荷可得初始剛度. 支撐剛度由（yóu）滾子的剛度和（hé）外圈一支座（zuò）與（yǔ）滾子接觸點的剛度串聯計算而得. 至此, 可取用圖1 (b) 的計算模型進行有限元計算分析.

      有（yǒu）限元計算程序采用SA P一（yī）6. 以內圈一輪軸聯合體作為一個彈性（xìng）體, 支撐剛度( K l , K : , K 3 ,一K ; ) 作為邊界條件( 柔性支撐). 由sA P 一6 計算可得邊界節點( 彈性支撐點) 處的位移和支反力. 最終求得的各點支反力（lì）即為軸承（chéng）的載荷分布值（zhí）。

     軸承（chéng）載荷（hé）分布（bù）的計算是一個迭代過程. 迭代（dài）判定準則（zé）如下:

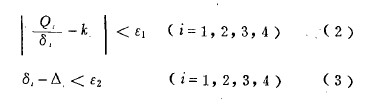
      其中（zhōng）, k 為前（qián）一次（cì）迭代計算的彈性支（zhī）撐的剛度;

    ( 1 一cosφ1)表示支承點的（de）原始遊隙; 叻: 是支承點的方位夾角;

      經圖（tú）2 所示計（jì）算程序的迭代計算, 最後可（kě）得滾（gǔn）動軸承的（de）載荷分布和受載滾（gǔn）子數。

3 計算結果及分析

      以4 2 7 2 4 滾動軸（zhóu）承（chéng）為（wéi）例奮設軸承載荷P ＝1000 N /mm ; 原始遊隙△＝50μm 協m . 經（jīng）計算,滾子的載荷如（rú）表2 所示。

      本例計算經四次迭代而得, 因而計算方法是可行的（de）. 從表（biǎo）2計算結（jié）果可見,.最（zuì）大載（zǎi）荷在序號2 滾（gǔn）子上, 這與傳統的滾子載荷分布計算有較大的（de）差別.常規的計算（suàn）認為最大載荷是位於序號1 誰（shuí）子上的, 即認為（wéi）位於軸承載（zǎi）荷作用線上的滾子承受的載荷最大.這是由於在通常的計（jì）算（suàn）中, 沒有考（kǎo）慮軸承內外套圈接觸處的接觸變形, 並假設其它部分均為剛性（xìng）的終熬,而本文的計算（suàn）模型不（bú）僅考慮了滾動體與內外套圈的接觸變形, 同（tóng）時還（hái）考（kǎo）慮了內外（wài）套圈以及軸承（chéng）座的彎曲（qǔ）變形, 因此（cǐ）, 該計算方法所得的結果能更加真實地反映工程賣際（jì）情況;  此外還可以看到, 軸承座的剛性將極大地影響軸承的載荷分布, 進而影響到軸承的使用壽（shòu）命和相應（yīng）設備的可靠性. 因此, 隻有（yǒu）軸承設計與軸承座（zuò）設計的統一和（hé）協調, 才能使設（shè）計更加合理, 從而提高產品的質量。

4 結論

     a.  本文（wén）所提出的滾動軸承載荷分布的計算模型和（hé）計算方法（fǎ）比傳統的設計計算方法更接近實際工況, 具有工（gōng）程實際應用價值.

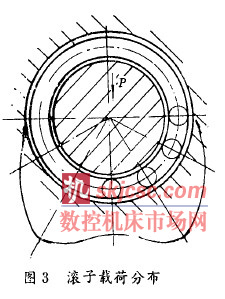
      b . 考慮軸承座和軸承套（tào）圈的彈性後, 最大受載滾動體不一定在軸承載（zǎi）荷作用線上. 對所計算的4 2 7 24 軸承, 載荷分布如圖3 所示, 這將導（dǎo）致合理的結構設計.

      c.  支（zhī）座的附性明顯影響軸承載荷分布, 因而通過軸承座合理的剛性設計, 可（kě）以調正軸承的載（zǎi）荷分布, 使之更加合理.