在（zài）五軸機床的NC 驗證中, 圖形法驗證顯然（rán）無法滿足五軸機（jī）床的複雜性, 這是由（yóu）圖形法驗證（zhèng）方法的（de）簡單性和粗糙性決定的。以布爾運算為特征的實體碰撞和幹涉檢驗方法, 隨著實體複（fù）雜程度的提高（gāo）, 布爾運算耗費時間和內存的特點（diǎn）也逐漸（jiàn）顯現出來。加工件逐步成型技術可以很好地仿真材料的切除過程, 但是複雜實體裁剪線段的算（suàn）法實現起來也是困難重（chóng）重。離散點法矢量切割檢驗（yàn）方法（fǎ）[ 6, 9] 用法矢量和刀具掃描體求交的方法進行NC 驗證, 此方法被認為是進行（háng）NC 驗證最精確的方法[10] , 對精度檢驗來說還（hái）是不可替代的方法（fǎ）[ 9] , 可以給出定量的精度信（xìn）息。該方法的（de）難點有兩個: 一是刀具掃描（miáo）體的構造和顯示, 二是射線和曲麵的求交算法。本（běn）文就（jiù）是針（zhēn）對這一NC 驗證算法, 對刀具掃描（miáo）體構造和顯示問題展開研究。

1　五軸刀具掃描體的運動特點

     現代數（shù）控機床（chuáng）加工複（fù）雜零件的過程一般如下: 首先（xiān）根據零件（jiàn）圖樣及工藝要求等原始條件計算刀位軌跡, 產生刀位原（yuán）文件, 然後經過後置處理把刀位原文件轉換成指定數控機床能執行（háng）的數（shù）控程序, 驅動相應的執（zhí）行機構進行加工。現（xiàn）代的數控（kòng）加工過程, 在零（líng）件正式（shì）加工之前都要進行NC 驗證。NC 驗證主（zhǔ）要關心的是刀具與零件的相（xiàng）對（duì）位置（zhì）關係, 這種關係或者直接由NC 程序（xù）來約束, 或（huò）者由刀位文件進行約束。由（yóu）於不同的數控係統具有不同的指令集（jí）, 由NC程（chéng）序直接（jiē）驅動的加工仿真需要後置處理過程的（de）配合, 對後置處理的研（yán）究超出了本文的研究範圍, 本文（wén）采（cǎi）用刀位文（wén）件來規定刀具與零件之間的相（xiàng）互關係。刀位文件具有一定的格式（shì）, 需要一個刀位解釋器對其進行處理, 從中提取出用於（yú）加工（gōng）仿真的刀位軌跡信息。刀（dāo）位軌跡信息主要包括刀心位置和（hé）刀軸方向。五軸機床由於增加了二個擺動軸, 使得刀（dāo）具的（de）刀軸矢量在加工過程中是變化的, 如圖1 所（suǒ）示。

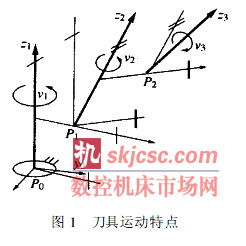
2　刀具掃描體的描述

    刀具掃描體就是刀具在加工過程中沿著加工軌跡運動時所掃過的空（kōng）間幾何實（shí）體。有（yǒu）許（xǔ）多文獻介紹過掃描體的生成[1, 2, 11, 12] , 它們的生（shēng）成方（fāng）法均（jun1）建立在微分方（fāng）程的基礎上,用數學方法（fǎ）求得（dé）曲麵包（bāo）絡麵方程, 因而生成的（de）算法比較複雜, 實現比較困（kùn）難, 運算速度較慢。其（qí）中W. P. Wang 和K. K. Wang 的方法具有代表性[ 1, 2] 。

    本（běn）文由五軸刀具（jù）掃描體的運（yùn）動特點出發, 把（bǎ）刀具（jù）掃描體看成是每兩個刀位點之間掃描體的連接, 形成一個（gè）完（wán）整的掃描體, 由於（yú）在五軸數控加工中, 一般隻采用直線插補,所以這種（zhǒng）假設是符合經（jīng）過後置處理後（hòu）得到的NC 程序運（yùn）行的實際（jì）情況的（de）。由於在運動過程中刀軸矢量是變化的, 刀具的各個部位掃過的表麵並不是平麵, 球頭刀的刀頭部分掃過（guò）的包絡麵也不是標準（zhǔn）的柱麵。在兩個（gè）連續的刀位點之間的包絡麵應該是一個掃描麵, 這個掃描麵是由（yóu）二維的邊界曲線或者直線沿著空（kōng）間某個方向運動形成的, 在這個運動過程中（zhōng）同時伴隨著回轉動作, 所以形成的包絡麵形狀頗為（wéi）複雜。用常規（guī）的拚合方法（fǎ）難以滿足（zú）造型（xíng）需要。

    非均勻有理B 樣條( NURBS ) 技術（shù）的出現, 使得（dé）無論對標準的解析（xī）形狀( 如圓錐曲（qǔ）線、二次曲麵、回轉（zhuǎn）麵等) 還是自由曲線、曲麵都提供了統一的（de）數學表示和統一的表示參數。這解決了實際（jì）應用中大量存在的各種類型曲麵並存, 但是沒有一個有效表示這些曲麵形狀的統（tǒng）一的數學（xué）方法的問題。本文以球頭圓柱刀（dāo）作為研（yán）究對象, 刀具在運動中, 球麵部分（fèn）掃過的曲麵可以看作是一個個的直紋麵銜接而成, 這（zhè）種（zhǒng）直紋麵不能（néng）用一般的體素造型方法很好的（de）表示, 利用非均勻有（yǒu）理B 樣條( NU RBS) 方法可以（yǐ）解決這一問題。但是由於（yú）構造該直紋麵的邊界曲線是一個半（bàn）圓（yuán）, 而NURBS 曲線是由控製點來表達的自由曲線, 從它的表達式（shì）不能簡單（dān）地推導半圓（yuán）弧的表示形（xíng）式。因（yīn）此有必要首（shǒu）先研究用NURBS 曲線表示圓弧的方法, 然後才能得出直紋麵的NURBS 表達式。

3　刀具掃（sǎo）描體構造（zào）新方法

    本節首先推（tuī）導刀具的球頭部分形成的掃描麵, 該麵是整個（gè）掃描體構造中最複雜的部分, 其（qí）它部分可以看成（chéng）是（shì）此（cǐ）部分曲麵的簡化, 可以按照此（cǐ）部分曲麵加以（yǐ）推導即可。刀（dāo）頭部分掃描（miáo）麵的邊界曲線（xiàn）是半圓弧, 3 次NURBS曲線能簡便地表示半圓弧, 方法如下:

    定理　若已知三次有理Bezier 曲線Ci( u) , 其控製頂點及其權分別為Ui , Ui+ 1, Ui+ 2, Ui+ 3; H i , H i+ 1, H i+ 2, H i+ 3。則它可以用三次NURBS 曲線

     由於刀具掃描體（tǐ）可以看（kàn）成是在三維空間經過掃描（miáo）所產生, 所以還必須求出掃描後產生的（de）掃（sǎo）描麵方程, 根據五軸機床刀位軌跡驅動的刀具掃描體的運動特點, 構造出（chū）的掃描麵應該（gāi）是（shì）NU RBS 曲（qǔ）麵, 把每二個刀（dāo）位點之間的運動看成（chéng）是（shì）二維圖形在空間（jiān）沿直線運動和回轉運動（dòng）的結合。

     已知空間兩點（diǎn）P 0, P1, 連（lián）接兩點的（de）直線可表示為

    根據上述NURBS 曲麵定義以及半圓（yuán）弧和直線的NU RBS 表示, 我們可以構造出球頭刀具（jù）的球（qiú）頭部分( 球頭也是刀具繞（rào）刀軸形成的包絡麵, 此點請引起注意) 在三維空間掃描形成的掃描體外表（biǎo）麵公式。令

    上（shàng）式為一條線段的NURBS 表示式。證明掃描麵是直紋麵。刀具（jù）掃描體的其餘部分包（bāo）括: 起始（shǐ）點（diǎn）的刀具原體, 它們是半球和圓柱體, 可（kě）以（yǐ）用B-rep 來表示（shì）。

3 仿真結果

    OpenGL 是（shì）一個工業標（biāo）準的三維計（jì）算機圖形軟件接口, 它的（de）GLU 庫函數提供了一個NURBS接口, 利用上麵推導出的結果, 結合CAD/ CAM 軟件生成（chéng）的刀位文件, 我們用VC 編寫了一個（gè）五（wǔ）軸刀具掃描（miáo）體的仿（fǎng）真（zhēn）軟件, 由圖3 中效果可以看出, 刀具掃描體的表麵（miàn）光滑, 各個離散的（de）掃描體的銜接連續, 能夠（gòu）反應真實的（de）刀具掃描體的包絡麵。