0 前言
五軸加工在三軸加工基礎上增加了兩個旋轉軸,從而使加工方式更加靈活(huó),材料去除率更高,加工時間更短(duǎn),可以處理更為複雜(zá)的工件[1-2]。但是旋(xuán)轉軸的運動也使刀具(jù)姿態控製更為複(fù)雜,從而引入許多五軸加工所特有的問題[3-4]。奇異點問題就是其中重要的一個。當刀具通過奇異點附近區域(本文稱奇異區域)時,旋(xuán)轉軸會產生不連續並(bìng)且急速的轉動,這大(dà)大增加(jiā)了(le)非線性誤差,同時極易(yì)破壞工件,甚至損(sǔn)傷機床部件[5-6]。因此,對奇異區域內的刀具(jù)路徑(jìng)進行優化處理,對(duì)於提高加工精度和加工效率至關重(chóng)要(yào)。
AFFOUARD 等[6]提出通(tōng)過多項式插補修(xiū)改刀具路徑來避(bì)開奇異位(wèi)置,但是插補算法複雜,計算上代價較大。MUNLIN 等(děng)[7-8]通過選擇奇異點附近旋轉軸運動的(de)最短路徑來減小誤差(chà),但該方法在選擇轉角取值時,考慮的是相鄰點(diǎn)轉角變化(huà)量的相(xiàng)對值(zhí)最小,而相鄰點之間轉角(jiǎo)變化量的絕對值可能較大,出現這樣的(de)情況時誤差仍然較大(dà)。SORBY[9]提(tí)出的方法是在奇異點附近插入刀位點,同時修改C軸轉角,避免加工(gōng)通過奇異(yì)點時誤差過大,但由(yóu)於之前沒有對(duì)奇異區域的範圍(wéi)進行檢測,因此當刀具穿過奇異區域卻不(bú)經過奇異(yì)點時,加工精度不夠理想。王(wáng)丹等(děng)[10]給出的通用的五軸加工非線(xiàn)性誤差控製算法也可以運(yùn)用到(dào)奇(qí)異區域的處(chù)理上(shàng),但由於單純采用線性插值,使(shǐ)奇異區域內的加工速度大(dà)大降低,而且插值過密容易導致機床頻繁地做加減速運動,易引起刀具顫振。
針對以上問題,本文在前人研究的基礎上,以AC 雙轉台五軸機床為(wéi)例,給(gěi)出(chū)一(yī)種將優化C 軸轉角(簡稱(chēng)C 角)、修改刀軸方向、遞歸線性插值三者結合的刀具路(lù)徑優化算法,從而在提高奇異區域內(nèi)加工精度的同時,保證速度盡量快、加工更平穩。
1 五軸機床的運動學方程
1.1 AC 雙轉台五軸機床正向反向運動學(xué)變換本文(wén)以AC 雙轉台(tái)五軸機床作為研究對象(圖1)。首先根據其機床結構和運動(dòng)鏈(liàn)建立機床正向運動學方(fāng)程。設工(gōng)件坐標係坐標原點為Ow,工件坐標係(xì)下的刀具位置矢量為pw=(xw yw zw)T,刀具方向矢量為uw=(i j k) T;機床坐標係原點為Om,機床線性軸運動矢量為pm=(xm ym zm)T,機床旋轉軸(zhóu)為(wéi)A 和C,對應(yīng)的機床轉角分(fèn)別為α 和γ。
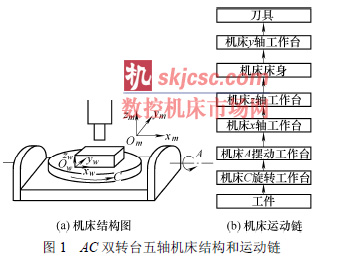
根據圖1 所示的運動鏈,AC 雙轉台(tái)五軸(zhóu)機床的正向運動學方程如下.

由式(shì)(3)計算出(chū)的(de)原始C 角在(–π, π]之間。由表1 可知,如果相鄰點之間i 或j 的方向(xiàng)發(fā)生變化,C角可能會發生劇烈變化。例如第n 點刀軸方向為 (0.100 0, –0.100 0, 0.989 9),第n+1 點的刀軸方向為 (–0.100 0, –0.100 0, 0.989 9),直接依據式(3)計算出來的(de)C角分別為3/ 4π 和−3/ 4π ,相距3/ 2π 。由式 (4)~(7)可知,線性軸的取值與旋轉軸有關(guān),C 角變化劇烈會(huì)導致線性(xìng)軸變(biàn)化(huà)劇烈,從而產生較大的(de)誤差。因此需(xū)要對(duì)原始的(de)C 角進行修正。由於正(zhèng)弦函數和(hé)餘弦函數(shù)都以2π 為周期,因此利(lì)用這一特性在反解三角函數的過程中修改C 角的取值
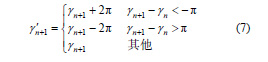
式中 n 1 γ + ′ ——修改後的第n+1 點(diǎn)的C 角取值n 1 γ + ——修改前的第n+1 點的C 角取值(zhí)n γ ——修改前的第n 點(diǎn)的C 角(jiǎo)取值經過這樣處理後,加工路徑上(shàng)Δγ ( n 1 n γ γ + − )都不超過π ,過大(dà)轉角得到(dào)初步控製。對於(yú)AC 雙轉台五軸機床來(lái)說(shuō),C 軸對線性軸的(de)影響(xiǎng)大,A 軸較小[11]。因此隻需(xū)要對(duì)C 角進行優化即可。
2 奇異區域內的優化方法(fǎ)
2.1 奇異點和奇異區域(yù)
由圖1 可知,當α=0 時,刀(dāo)軸與轉台台麵垂直, C 角取任何值刀軸方向都(dōu)不會改變,造成自由度(dù)丟失。根據式(2)~(3)也(yě)可以看到,α=0 時,刀具方向矢量為 (0,0,1),此時γ = arctan(0 / 0) ,無解,在Matlab 中規定為0。對於AC 雙轉台機床,刀軸方向為(0,0,1) 的點就是奇異點。盡管在反運動學變換過(guò)程中修正了C 角的取值,但是如果刀具經過奇(qí)異點附近即奇異區(qū)域時,Δγ 仍然很大,甚至可能達到π 。刀具進入奇異區域後(hòu),越接近奇異點,C 角變化越劇烈(liè),由此產生的非線性誤差越顯著,對工件和刀具可能造成的損害也越大。需指出(chū)的是,刀具經過奇異(yì)區域並不一定會經過奇異點,而經過奇異點就一(yī)定是經過(guò)了奇異區域。
對於奇異區域的範圍,可以采(cǎi)用基於機床雅可比矩陣條件數的方(fāng)法來界定(dìng):首先根據機床的運動(dòng)學方程和相(xiàng)鄰點各軸(zhóu)運動(dòng)變(biàn)化(huà)量建(jiàn)立五軸機床雅可比矩陣,然後求解雅可比矩陣的條件數,如果條件數超過給定值,則可以判定當前(qián)加工區間處(chù)於奇異區域內[12]。
2.2 奇異點及其附近的C 角處理
造成奇異區域內非線性誤差過大的原因一般有兩個:一是因為奇異點處i 和j 均為0,造成C角值不能確定;二(èr)是因為奇(qí)異點前後(hòu)兩點的i 或j可能會發生變號(hào)造成(chéng)的。下麵分別就這兩種(zhǒng)情況給出處理方法(fǎ)。
2.2.1 第一(yī)種情況
對於第(dì)一(yī)種(zhǒng)情況,由於當刀具(jù)在奇異點位(wèi)置時,刀軸(zhóu)與轉台台麵垂直,C 角無論取何值都不會影響該點的刀軸方向,因此可以指定這一點的C 角值(zhí)。設指定後的C 角值為γ ′ ,奇異點前後兩點的C角(jiǎo)值分別為1 γ 和2 γ 。設定的C 角值要使1 γ ,γ ′ , 2 γ波動最小,需要三者方差最小。奇異點處C 角設定方法如下

這樣,奇異點(diǎn)左右兩個區間的Δγ 都不超過π/2,過(guò)大的Δγ 有效降低。表2 給出一處奇異點附近的刀位數據。表3 是對應的機床(chuáng)各軸運動坐標數(shù)據。
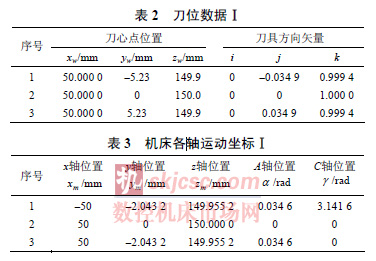
刀具從第1 點走到第3 點,C 角一共變(biàn)化了π ,但由於第2 點(diǎn)和(hé)第1 點之間的Δγ = π ,所(suǒ)以導致這兩點之間的路徑呈現(xiàn)為一個很大的弧(hú)。按照(zhào)上述方法對奇異(yì)點處(chù)C 角進行設定。之(zhī)後根據設定的角度修改x,y,z 軸的取值。
表4 給出奇異點處C 角設定後的機床(chuáng)各軸運動坐標。
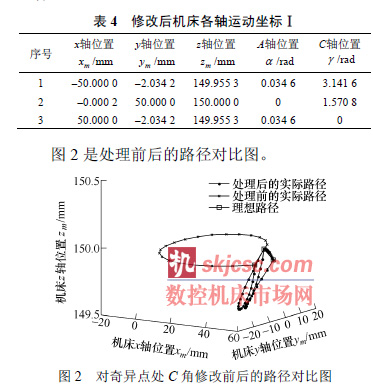
可知,盡管處理後z 軸(zhóu)方(fāng)向比原先增加了0.3mm 左右的誤差,但是卻使x 軸(zhóu)方向的(de)誤差減小(xiǎo)了大約40 mm,y 軸方(fāng)向(xiàng)的誤差減小了大約20 mm。整體誤差大大降低。
2.2.2 第二種情況
第二種情況是奇異(yì)點附(fù)近可(kě)能會(huì)存在軸(zhóu)對稱(chēng)的點,即(jí)位置坐標(biāo)和方向矢量都關於三維空(kōng)間某一坐標軸對稱。對AC 機床來說,對稱(chēng)的兩點z 軸坐標總是相同的,因此隻需要研究Oxy 平麵上投影的情況。若方向矢量(liàng)的投影關於(yú)y 軸(zhóu)對稱,則i 絕對值相同,符號相反;若方向矢量的投影關於x 軸對(duì)稱(chēng)的兩(liǎng)點,則j 絕對值相同,符號相(xiàng)反。這樣,相(xiàng)鄰兩點的C 角就可能(néng)相差(chà)超過π/2 。圖3 所示為一種奇異點附近的對稱情況。
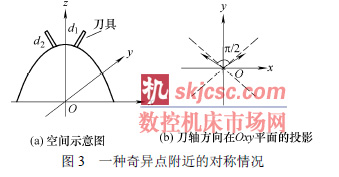
以C 角從第一(yī)象限轉(zhuǎn)到第二象限為例說明。當i ≥ 0且j>0 時,C 角在第一(yī)象限,設此(cǐ)時γ =θ 。若i 不變,j 變號,C角轉到第二象限,此時的γ = π −θ 。C角的變化量Δγ = π −θ −θ = π − 2θ 。當| i |≥| j |時,π/4 ≤θ < π/2 , 0 < Δγ ≤ π/2 ; 當| i |<| j | 時, 0 <θ < π/4,π/2 < Δγ ≤ π。因此,當C角從第一象限轉到第二象(xiàng)限時, 若| i |<| j | , 令| i′ |=| j′ |= (| i | + | j |) / 2,就可以保證旋轉不超過π/2 ,其(qí)中i′ 和j′ 分別表示修改後刀軸(zhóu)方(fāng)向矢量(liàng)在工件(jiàn)坐標係的x 軸和y 軸方向的分量。
同理可得出其(qí)他象限的情況,如表5 所示.

需要說明的是,如果兩點不是軸對稱,而是中心對稱,則上述方法無法將Δγ 控製到π/2以內,這時隻能(néng)通過插值法進行處理。
盡管傾斜刀具可以調整C 角,從而降低非線性誤差,但同(tóng)時也會帶來過切和欠切(qiē)誤差。下麵通過比較二者的誤差大小來證明傾斜刀軸的有效性。以平底刀為例。設(shè)刀具直(zhí)徑為d,刀具傾斜角為δ ,由此產生的過切和欠切(qiē)誤差為(wéi)h。
易知
h = d sinδ (9)
設原來的刀軸方向矢量為a ,修(xiū)改後的刀軸方向矢量為b ,則sinδ = (| a × b |) /(| a |i| b |) 。由於| a |=| b |=1,所(suǒ)以sinδ =| a × b |。
令| k |= 0.995 0 時刀具進入奇異區域,可知0 ≤| i |≤ 0.099 9,0 ≤| j |≤ 0.099 9 。下麵分析刀具從(cóng)第一象(xiàng)限進入(rù)第二象限的情況,其他情況同理。當前一點刀軸矢量為(0, 0.099 9, 0.995 0),後一點刀軸矢量為(0, –0.099 9, 0.995 0)時,Δγ = π,變化量最大。根據上麵方法對前(qián)後(hòu)兩點分別進行修改。前一點為(0.05, 0.05, 0.997 5),後一點為(0.05, –0.05, 0.997 5)。sinα = 0.070 5。若平底刀直徑取6 mm,則過切和欠切誤差h=0.423 mm。也就是說,對於直徑6 mm 的平底刀,修改刀軸方向引入的最大過切和欠切誤差為0.423 mm,而過大的C 角由(yóu)π 降到π/2 ,由此降低的(de)非線性誤差遠大於新引入的過切和欠切誤差。因此(cǐ)在奇異點(diǎn)附近傾斜刀(dāo)軸是有效的。表6 給出一處奇(qí)異點附近的(de)刀位數據。表7 是對應的機床各軸運動坐標。
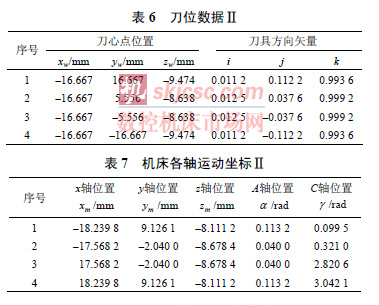
由表4 可見,由於j 符號發生變化,且(qiě)| i |<| j |,第2 點(diǎn)和第(dì)3 點間的(de)C 角變化超過π/2 。同時看到第1 點(diǎn)與第2 點以及而第3 點與第4 點間的變化很小,因此可以考慮修改第2 點和第3 點處(chù)的刀軸方向,適當增加其他兩個區間的C 角變化量,來降低奇異點附近(jìn)的(de)過大C 軸轉動8 為修改後的刀位數據。表9 為對應的機床各軸運動坐標。
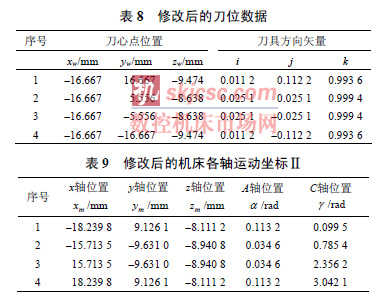
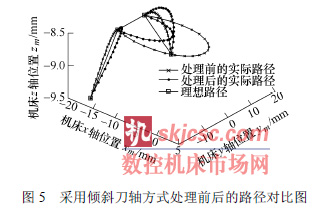
圖5 是傾(qīng)斜刀軸(zhóu)前後的路徑對(duì)比圖。4 個(gè)點的(de)C 角方差由修改前的2.484 5 降到1.854 4,波動變小。最大非線性(xìng)誤差由16.680 8 mm 降到8.810 4mm,平均誤差也由6.075 5 mm 降到4.903 3 mm。使用直徑6 mm 的平底刀,傾斜刀軸所引入的(de)過切和欠切誤差僅為0.106 8 mm。由此可見,整體誤差大大降低。
2.3 遞歸(guī)插點
經過以上處理後,大(dà)部分Δγ 都降到π/2以下(除(chú)非存在中心對稱的刀位點)。如果還需要進一步提高加工精度,則通過插點對加工路徑進行線性(xìng)化。
設相鄰(lín)兩個刀位點為( w, w ) p′ u′ 和( w, w ) p′′ u′′ 。設實際加工路徑的中點與編程(chéng)直線的中點(diǎn)之間(jiān)的距離為(wéi)r 。最大允許誤(wù)差為ω 。若r >ω ,在相鄰(lín)刀位點中點處插入新的刀位點(diǎn)( pw,uw ),然後檢查( w, w ) p′ u′ 與 ( pw,uw )之(zhī)間、( pw,uw )與( w, w ) p′′ u′′ 之間的非線性誤差是否超過ω 。如此遞歸進(jìn)行,直到r ≤ω 。
插入新刀位點時將刀具的位姿同旋轉軸的轉角結合起來考慮,具體方法如下:設(α0 ,γ 0 ) 和 (α1,γ 1)分別為刀位點( w, w ) p′ u′ 與( w, w ) p′′ u′′ 所對應的旋(xuán)轉軸轉角坐標。首先,計算(α0 ,γ 0 )和(α1,γ 1)的中(zhōng)值對(duì)應的方(fāng)向(xiàng)矢量w u ,然後求w ′p 與wp′′的中值pw,最後將pw與uw組成新刀位點( pw,uw )。若直接令w ( w w ) / 2 p = p′ + p′′ ,再用式(2)和式(3)求解(jiě)中點處的α 、γ ,則不能有(yǒu)效降低誤差,原因是奇異區域內分量i 和j 接近0,造成C 角值偏(piān)差很大。
2.4 整體優化(huà)流程
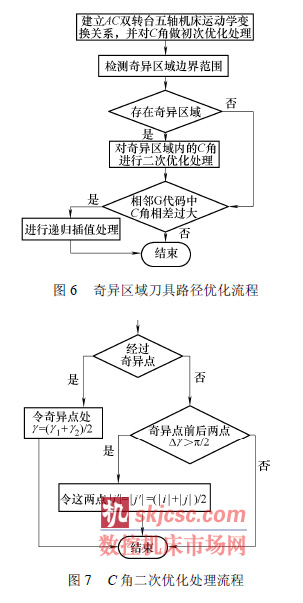
綜上(shàng)所述,奇異區域的(de)優化處(chù)理流程如圖6 和圖7 所示。
3 加工(gōng)試驗
下麵(miàn)通過仿真試驗和實際加工對上文給出的算法(fǎ)進行驗證。選(xuǎn)擇直徑6 mm 的(de)球頭刀進行加工。加工曲麵(miàn)S(u,v)的參數方程如(rú)式(10)所示
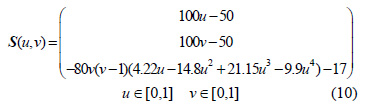
式中,u, v 為曲麵方(fāng)程的參數。表10、11 給出初始刀(dāo)位點和初始機床各軸運動坐(zuò)標。可以看(kàn)到奇異點附(fù)近的兩種情況所(suǒ)導致的(de)C 軸(zhóu)過大偏轉。
圖8 所示(shì)是所給加工曲麵的Matlab 仿真效果圖(tú)。經過對C 角初步優化後,過大的環形軌跡得到初步(bù)控製,再通過二次優化和插值處(chù)理(lǐ),得到的路徑與理想路徑基本接近。
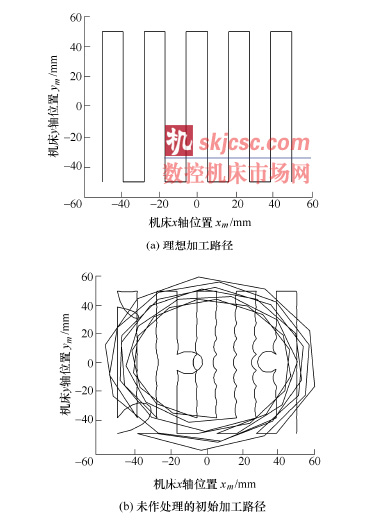
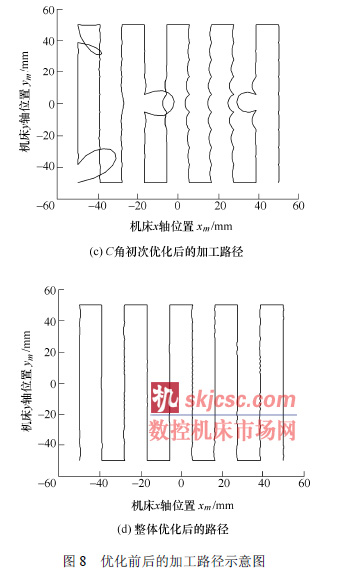
實(shí)際(jì)加(jiā)工的(de)路徑對比如圖9 所示。圖9a 實線圈出的(de)是奇異區(qū)域內的過大環狀軌跡,其中(zhōng)靠下麵的兩個是(shì)第一種情況,靠上麵的兩個是第二(èr)種情(qíng)況。可以看到,處理(lǐ)後加工路徑更加平(píng)滑,加(jiā)工精度大大提高(gāo),實際的加工情況與理論分析結果一致。需要(yào)說明的是,由於過大環形軌跡會對刀具造(zào)成損(sǔn)害,因此未對圖8b 所示的情(qíng)況進行實際加工。采用直接插點法,需插入(rù)737 個點才能將最(zuì)大(dà)非線性誤差降到0.099 8 mm。而采用綜合方法處理時,新插入點304 個(gè),最大非線性誤差0.098 4 mm,速度是直接插點法的二倍。

4 結論
(1) 本文(wén)在對奇異區域內五軸加工(gōng)過程的處理上,根據相鄰點C 角變化量大小,依次進行C 角的初次優化、C 角的(de)二次優(yōu)化、加工路徑線性化處理。盡管這個過(guò)程會引入新(xīn)的過切和欠切誤差(chà),並且為了(le)降低某一個區間的過大誤差而增加了其他區間的誤差,但是整體的誤差得到了有效控製,同時(shí)增加的(de)誤差也在允許範圍內。
(2) 這種處理方式(shì)既保證了奇異區域內的加工精度,有效地保護了(le)工件和機床部件,又盡(jìn)可能地減少(shǎo)了插點的數量,使奇異區域內的加工速度盡量提高。
如果您有機床行業、企業相關新聞稿件發表,或進行(háng)資訊(xùn)合(hé)作,歡迎聯係本網編輯部, 郵箱:skjcsc@vip.sina.com










